7.1 格的基本概念
7.1.1 格的定义
定义7.1 设是偏序集,对
,子集
在
中存在最大下界(下确界)记作
和最小上界(上确界)记作
;则称
为格。
多个元素当然也是同理的;
全序集肯定是格。
上确界和下确界具有唯一性。
定义7.2 设是一个格,若
上定义两个二元运算
和
,使得
,
等于
和
的下确界,
等于
和
的上确界。称
为由格所诱导的代数系统。
称为交运算,
称为并运算。
与环有一点相似。
小小总结以下:
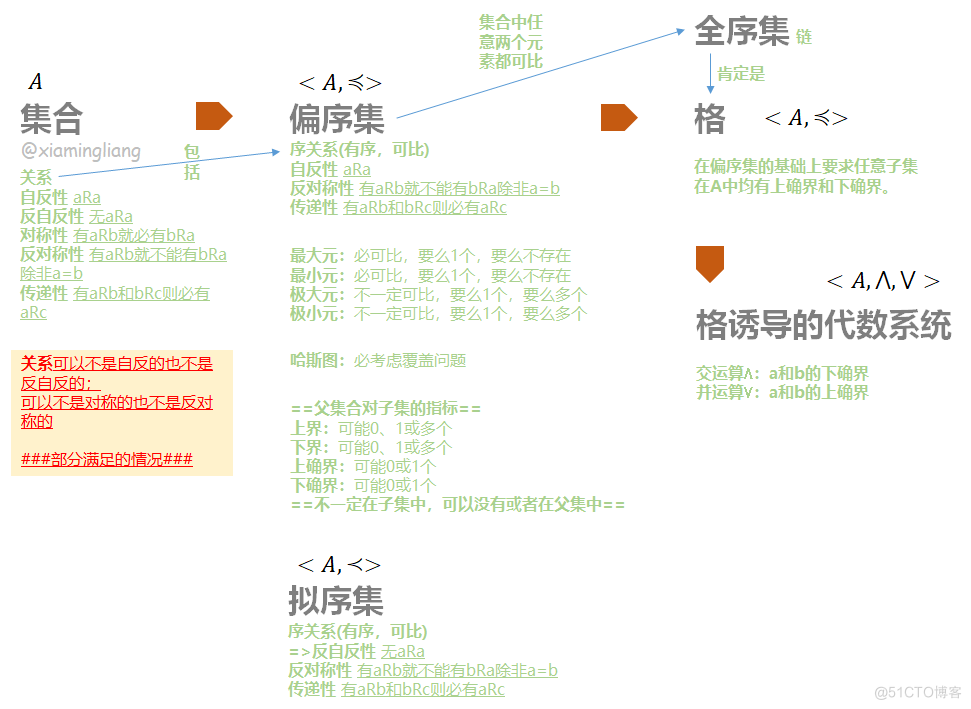
定义7.3 设是格,
是由格中的元素及
等符号所表示的命题;若将
中的
分别替换为
得到命题
称为
的对偶命题,简称对偶。
例7.3 判定下图偏序集是否为格。
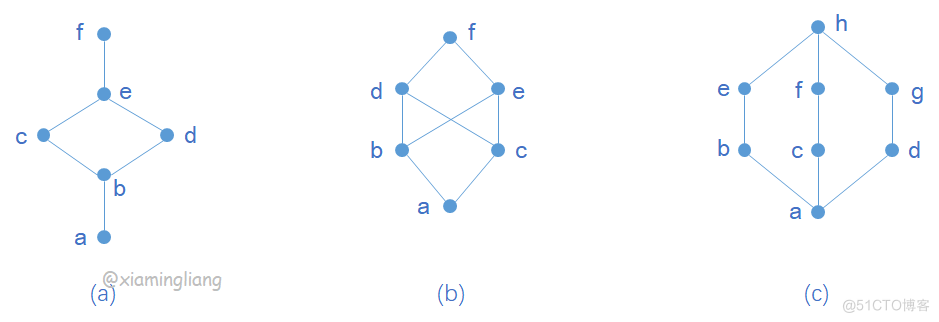
解:
(a)是格;因为任意两个元素在图中都能找到他们上和下确界;比如:
上确界:d
下确界:a
(b)不是格;因为存在两个元素在图中找不到他们的上或下确界;比如:
上确界:无(d和e之间不可比,无法判定它们谁最小)
下确界:a
(c)是格;因为任意两个元素在图中都能找到他们上和下确界;比如:
上确界:h
下确界:a
7.1.2 格的性质
定理7.1 在一个格中对
都有:
根据定义7.2知:
是
和
的上确界;
是
和
的下确界。
定理7.2 设是格,
,则有:
(1) 且
可得
(2) 且
可得
是
和
的下界;
又
和
的最大下界(下确界)是
;
因此
定理7.3 在格中,对于
,若
,则
且
。
定理7.4 设是一个格,由它所诱导的代数系统
,则对
有:
(1)交换律:
(2)结合律:
(3)幂等律:
(4)吸收率:
定理7.5 设是一个代数系统,其中
和
都是二元运算,且满足交换律、结合律、吸收率;则
上存在偏序关系,使
是一个格,且
有
。
定义7.4 设是代数系统,其中
和
是二元运算,若
和
满足交换律、结合律、吸收率;则称
是一个格。
定理7.6 设是格,则:
(1),若
则
(2),若
且
则
7.2 分配格与有补格
7.2.1 分配格
定义7.6 设是格,若
,满足:
则称是分配格。
在格的基础上满足分配律。
例 判断下图中的是不是分配格
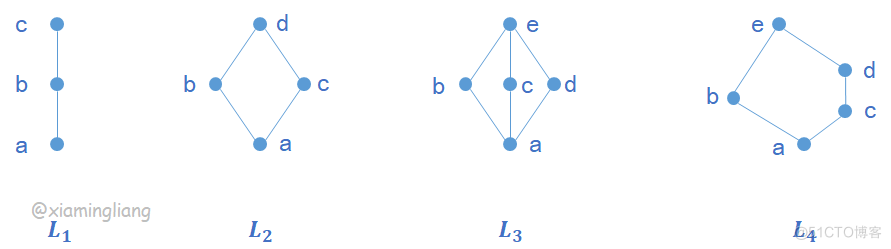
解:
和
是分配格;
和
不是分配格。
而
而
定义7.7 设和
是两个格,由它们分别诱导的代数系统
和
;若存在一个从
到
的映射
,使得
有:
称为从
到
的**格同态**,也称
是
格同态象。
若为双射时,格同态也称格同构。
定理7.7 格是分配格,当且仅当
中不含有钻石格或五角格同构的子格。
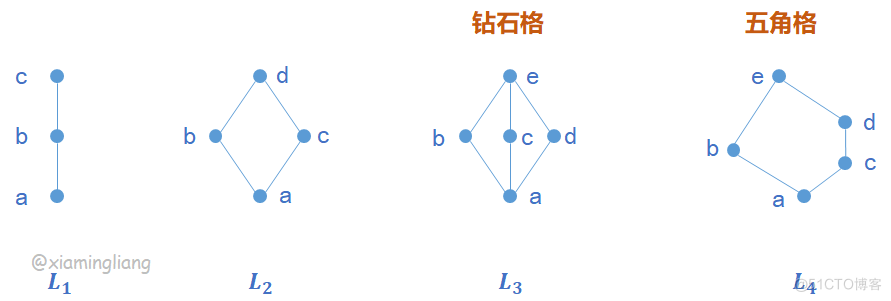
推论7.1
(1)小于5元的格都是分配格。
(2)任意一条链都是分配格。
链就是全序集。
7.2.2 有补格
定义7.8 设是一个格,如果存在元素
,对于
,都有
,则称
为格
的全下界;若都有
,则称
为格
的全上界。
全下界就是最小元,用0表示;
全上界就是最大元,用1表示。
定义7.9 设是格,若
存在全下界和全上界,则称其为有界格,记作
。
钻石格和五角格都是有界格,同时任何有限格
也都是有界格。设
则:
是
的全下界;
是
的全上界。
例7.8 设有限集,那么在格
中,空集
是其全下届,集合
就是其全上界。
定义7.10 设是有界格,
,若存在
,使得
且
,则称
是
的补元。
的补元记作:
或
。
显然,是
的补元,那么
也是
的补元;也就是
和
互补,简称互补。
在任何有界格中全下界
与全上界
总是互补的;集合中的其他元素则可能存在补元也可能无补元,当有补元时补元也可能不是唯一的。
对于有界分配格,若集合中的元素存在补元,则补元必定唯一。
定理7.8 设是有界分配格,若
,且对于
存在补元
,则
是
的唯一补元。
定义7.11 设是一个有界格,若对于
,在
中都有
的补元存在,则称其为有补格。
再次汇总下关系:
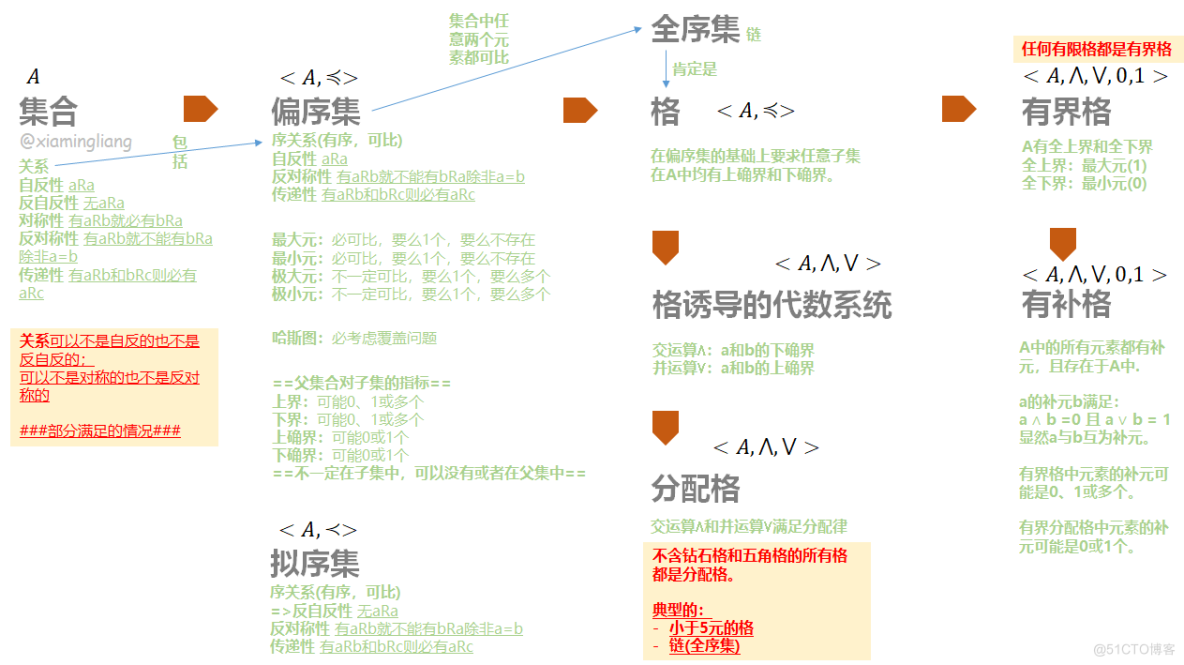
例7.9 判断下图中四个格的性质
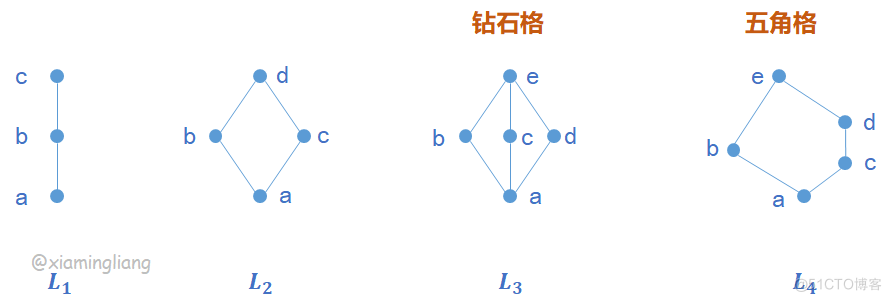
解:①找到格的全上界:1和全下界:0;它们必定互补。
②逐个找到其他元素的补元
:
全上界:,全下界:
;是有界格。
与
互补,
在格中不存在补元;因此本格不是有补格。
:
全上界:,全下界:
;是有界格。
与
互补,
与
互补;因此本格是有补格。
:
全上界:,全下界:
;是有界格。
与
互补,
中任一元素与剩余两个元素都互补,即每个元素都有2个补元;因此本格是有补格。
:
全上界:,全下界:
;是有界格。
与
互补,
的补元是
和
,
和
的补元是
;因此本格是有补格。
7.3 布尔代数
定义7.12 若一个格是有补分配格,则称它为布尔格或布尔代数。()
分配格中,若某元素存在补元那么它的补元是唯一的。
故在布尔代数中,每个元素都存在唯一的补元。
一般地,将求补元的运算(一般记作
)看作是布尔代数中的一元运算。
再次汇总下关系:
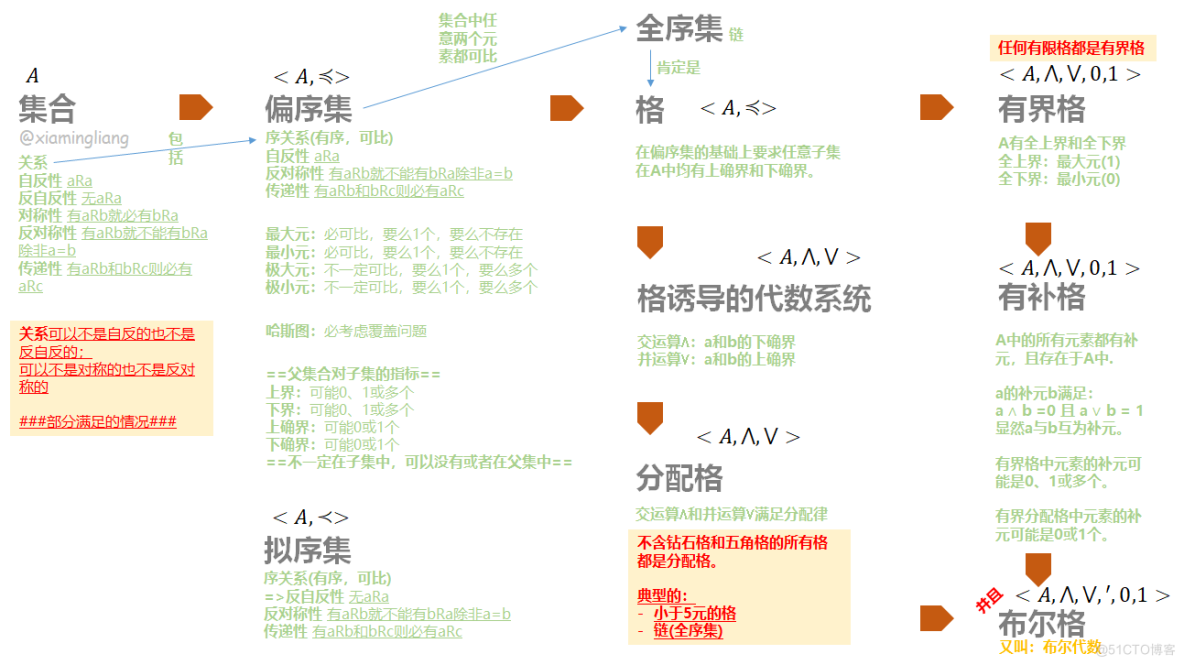
定理7.9 设有代数系统,其中
至少包含两个元素,
和
是
上的两个二元运算,
是
上的一元运算,对
,满足:
①交换律:
②分配律:
③同一律:在中存在零元
,使
##这里不要理解为求上界和下界
在中存在幺元
,使
##这里不要理解为求上界和下界
④补元律:,使
则是布尔代数。
定义7.13 设是代数系统,
,
是
上的二元运算,
为
上的一元运算,运算满足定理7.9中的①②③④条件时,则此代数系统为布尔代数。
废话!!!
定理7.10 设是布尔代数,则:
①
②

















