###纲要
-
排队现象与排队系统;
-
排队模型与系统参数;
-
排队系统时间参数分布规律;
-
排队系统的生灭过程与状态转移方程;
-
排队系统分析;
- 单服务台负指数分布模型
- 多服务台负指数分布模型
-
排队系统优化分析;
排队论发源于上世纪初。
当时美国贝尔电话公司发明了自动电话,以适应日益繁忙的工商业电话通讯需要。这个新发明带来了一个新问题,即通话线路与电话用户呼叫的数量关系应如何妥善解决,这个问题久久未能解决。
1909年,丹麦的哥本哈根电话公司A.K.埃尔浪(Erlang)在热力学统计平衡概念的启发下予以解决了。
##1.1排队现象与排队系统
###一、排队现象
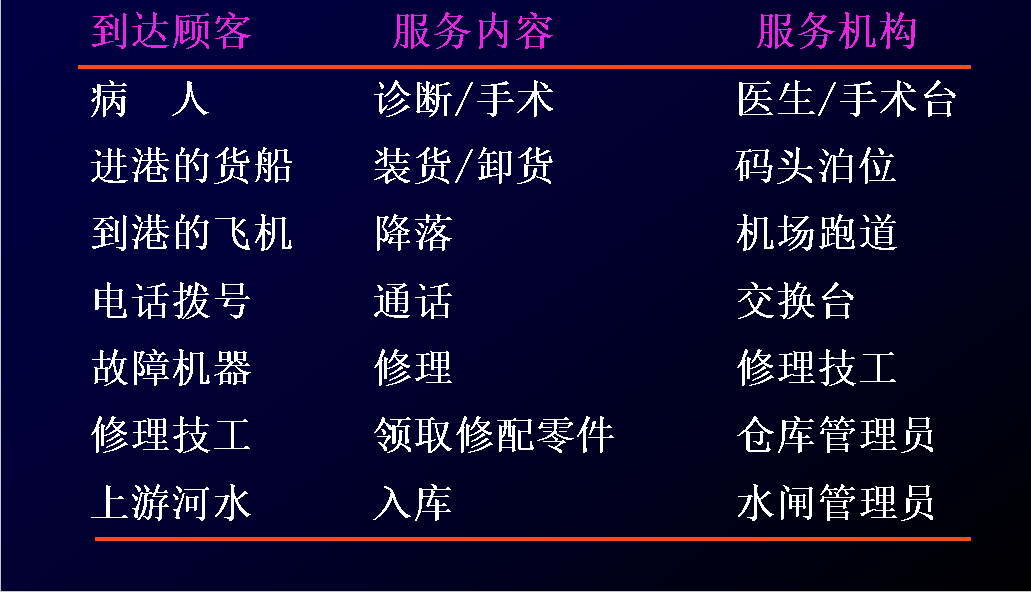
(1) 由于顾客到达和服务时间的随机性,
现实中的排队现象几乎不可避免;
(2) 排队过程,通常是一个随机过程,
排队论又称“随机服务系统理论”;
###二、排队系统
(一)排队服务过程

(二)排队系统的要素及其特征
-
排队系统的要素:
(1) 顾客输入过程;
(2) 排队结构与排队规则;
(3) 服务机构与服务规则; -
排队系统不同要素的主要特征:
(1)顾客输入过程
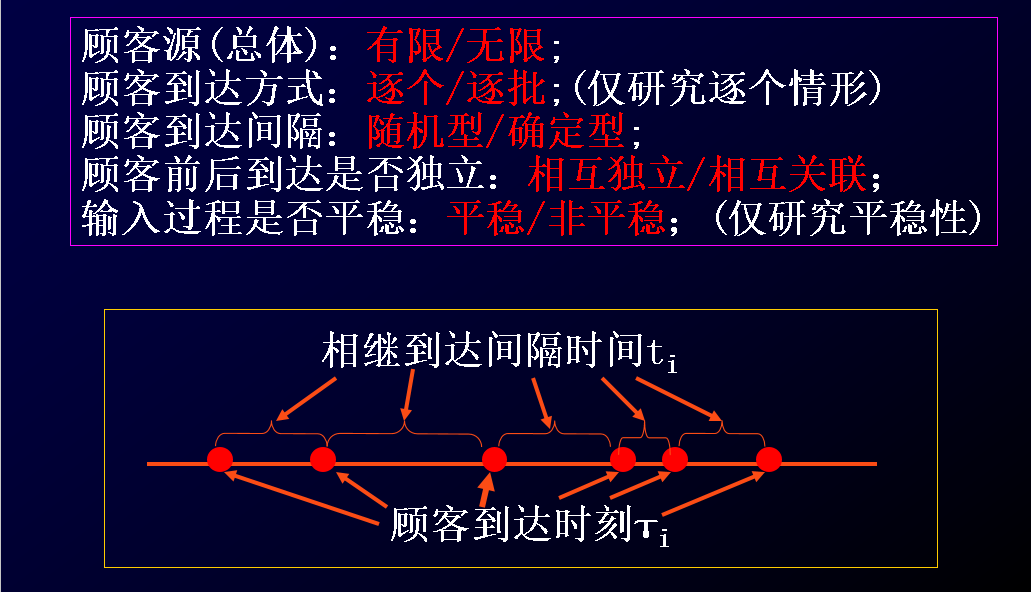
(2)排队结构与排队规则

(3)服务机构与服务规则
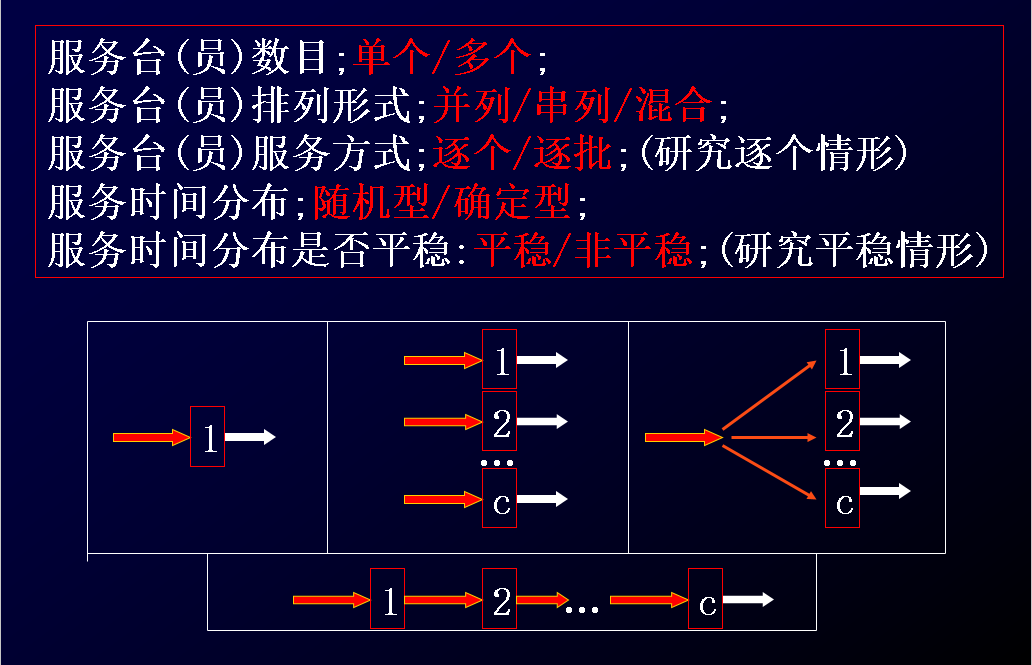
服务台(员)为顾客服务的顺序:
- a) 先到先服务(FCFS);
- b) 后到先服务(LCFS);
- c) 随机服务;
- d) 优先服务;
##1.2排队模型与系统参数
###一、排队模型
(一)排队模型表示方法


——略去后三项,即指 “**X/Y/Z///FCFS**”;
——这里仅研究FCFS的情形;
(二)到达间隔和服务时间典型分布
(1)泊松分布 **M** ;
(2) 负指数分布 **M** ;
(3) k阶爱尔朗分布 **Ek**;
(4) 确定型分布 **D**;
(5) 一般服务时间分布 **G**;
(三)排队模型示例
——M/M/1,M/D/1,M/ Ek /1;
——M/M/c, M/M/c//m,
——M/M/c/N/ ,。。。
##2.1、系统参数
###(一)系统运行状态参数
####1、系统状态 N(t)
——指排队系统在时刻t时的全部顾客数 N(t),
包括“排队顾客数”和“正被服务顾客数”;
——系统状态的可能值如下:
(1)系统容量无限制, N(t) =0,1,2,…;
(2) 系统容量为N时, N(t) =0,1,2,…,N;
(3) 服务台个数为c/损失制, N(t) =0,1,2,…,c;
一般,系统状态N(t)是随机的。
####2、系统状态概率:

——一般,排队系统运行了一定长的时间后,系统状态的概率分布不再随时间t变化,即初始时刻(t=0)系统状态的概率分布(Pn(0) ,n>>0)的影响将消失。
###(二)系统运行指标参数
——评价排队系统的优劣。
####1、队长与排队长

####2、逗留时间与等待时间
(1)逗留时间:
——指一个顾客在系统中的全部停留时间; 期望值,记为 Ws
(2)等待时间:
——指一个顾客在系统中的排队等待时间;期望值,记为 Wq
**Ws = Wq + E[服务时间]**
####3、其他相关指标
(1)忙 期: 指从顾客到达空闲服务机构起到服务
机构再次空闲的时间长度;
(2)忙期服务量:指一个忙期内系统平均完成
服务的顾客数;
(3)损失率: 指顾客到达排队系统,未接受服务
而离去的概率;
(4)服务强度: = /c ;
##3 排队系统时间参数分布规律
###一、顾客到达时间间隔分布
####(一)泊松流与泊松分布
如果顾客到达满足如下条件,则称为泊松流:
(1) 在不相互重叠的时间区间内,到达顾客数相互独立(无后效性).
(2) 对于充分小的时间间隔内,到达1个顾客的概率与t无关,仅与时间间隔成正比 (平稳性):
(3) 对于充分小的时间间隔,2个及以上顾客到达的概率可忽略不计 (普通性)。

####(二)泊松流到达间隔服从负指数分布

###二、顾客服务时间分布
####(一)负指数分布

####(二)爱尔朗(Erlang)分布

##3.1 排队系统的生灭过程
###一、排队系统的生灭过程
####(一)生灭过程的背景与定义

####(二)生灭过程状态变化的性质

####(三) 排队系统的生灭过程
(1)生灭过程示意
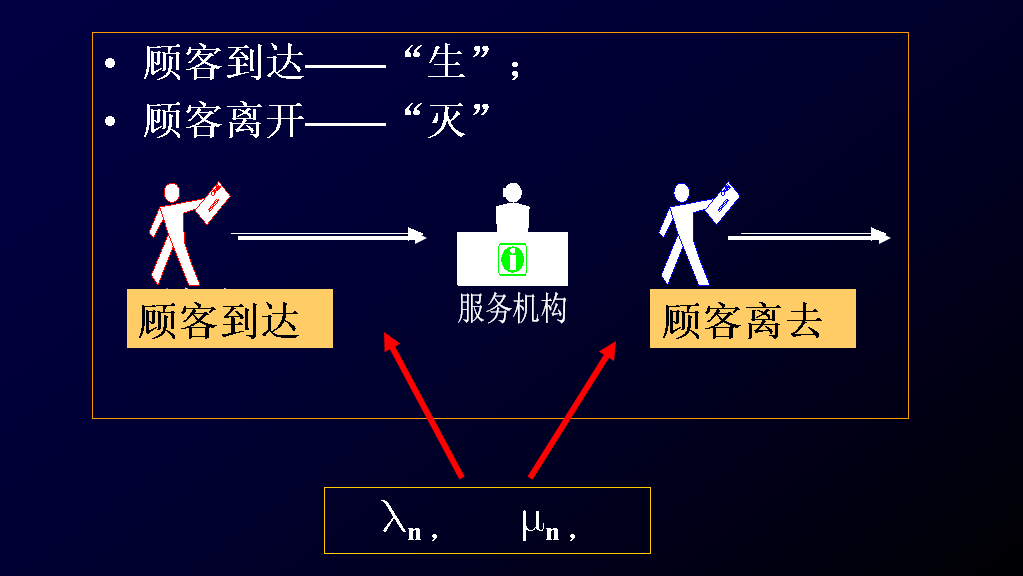
(2)生灭过程定义

##4 典型排队系统分析
排队系统性能参数的一般关系 ——Little 公式

##4 .1 单服务台负指数分布M/M/1排队系统
. 模型的条件是:
1、输入过程――顾客源是无限的,顾客到达完全是随机的,单个到来,到达过程服从普阿松分布,且是平稳的;
2、排队规则――单队,且队长没有限制,先到先服务;
3、服务机构――单服务台,服务时间的长短是随机的,服从相同的指数分布 。
对于M/M/1模型有如下公式:

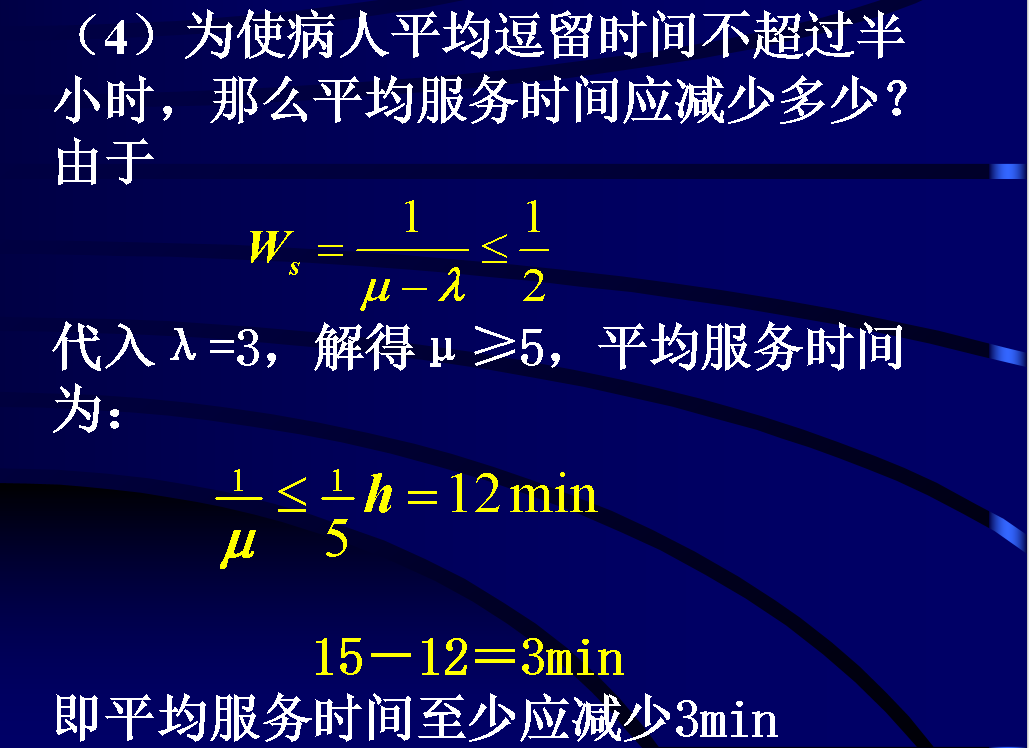
####例1
某医院急诊室同时只能诊治一个病人,诊治时间服从指数分布,每个病人平均需要15分钟。病人按泊松分布到达,平均每小时到达3人。试对此排队系统进行分析。





##4 .2 多服务台负指数分布M/M/S排队系统

####1、状态概率
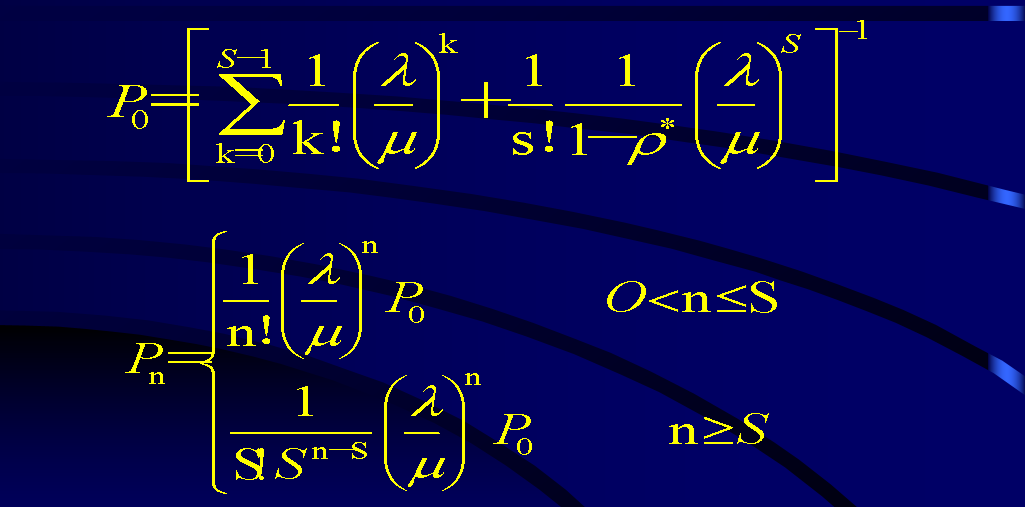
####2、主要运行指标
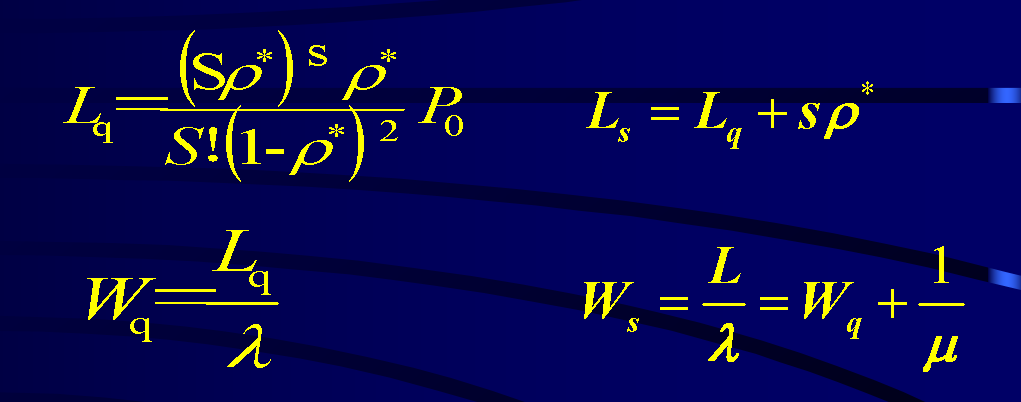
####3、系统状态N ≥S的概率
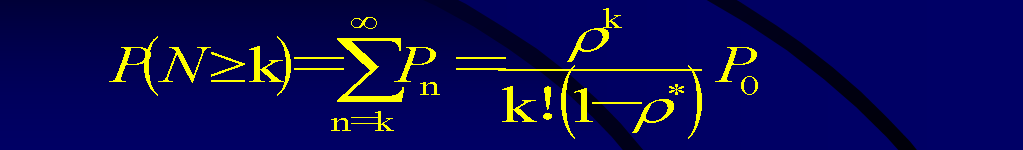
####例2
承接例1,假设医院增强急诊室的服务能力,使其同时能诊治两个病人,且平均服务率相同,试分析该系统工作情况。

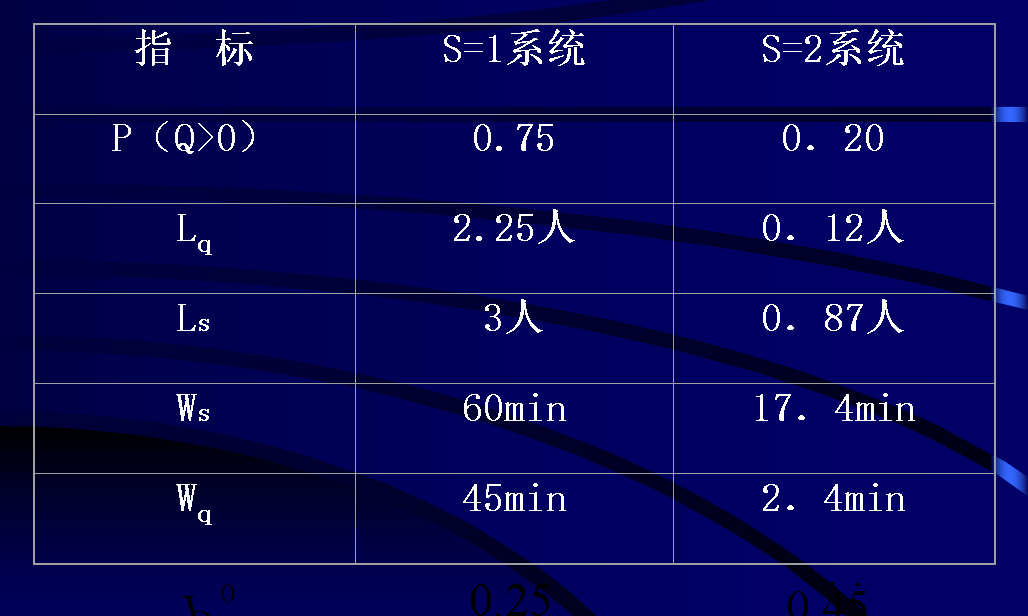
####例3
某医院挂号室有三个窗口,就诊者的到达服从泊松分布,平均到达率为每分钟0.9人,挂号员服务时间服从指数分布,平均服务率每分钟0.4人,现假设就诊者到达后排成一队,依次向空闲的窗口挂号,显然系统的容量和顾客源是不限的,属于M/M/S型的排队服务模型。求:该系统的运行指标 ?


























 334
334











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










