曼哈顿距离
曼哈顿距离和欧式距离一样是一种距离度量标准,不同的是它定义在L1范数下,也即用绝对值来衡量两点之间的距离。在一维空间下,曼哈顿距离定义如下:
d
(
x
,
y
)
=
∣
x
−
y
∣
d(x,y)=|x-y|
d(x,y)=∣x−y∣
在二维空间下,曼哈顿距离定义如下:
d
(
x
,
y
)
=
∣
x
1
−
y
1
∣
+
∣
x
2
−
y
2
∣
d(x,y)=|x_1-y_1|+|x_2-y_2|
d(x,y)=∣x1−y1∣+∣x2−y2∣
类似的,我们可以获得在n维空间下的曼哈顿距离定义。
最小化一维曼哈顿距离
有了距离定义之后,我们看一个有趣的问题:给定n个一维空间下的点,求使
∑
∣
x
i
−
a
∣
\sum{|x_i-a|}
∑∣xi−a∣最小的点
a
a
a。针对该问题我们有明确的答案:
a
a
a的取值就是
n
n
n个点的中位数。在quora上有一个比较浅显易懂的解释:在笔直的公路上种了n颗树,假设我们从中间颗树的位置开始往两个方向走,我们会发现不管往哪个方向走,我们都距离至少n/2颗树越来越远,而距离至多n/2颗树越来越近,所以上述距离总是在变大,从而说明使上述距离最小的点是中位数。下面给出数学证明:
我们假定使上述距离最小的点可以出现在数轴任意位置,既可以是n个点中的任意一个,也可以不属于n个点,我们分这两张情况讨论:
- 假设n个点已排序,选择第k个点计算距离,则有
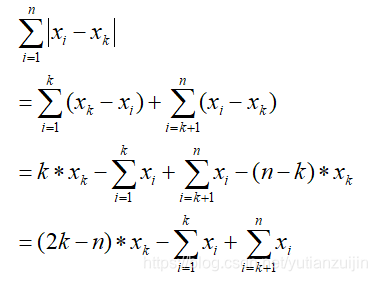
同理,选择第k+1个点计算距离,则有
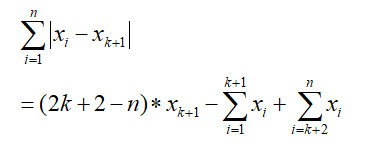
我们想知道当k逐渐变大时,距离的变化趋势,所以我们将上述两个距离做差
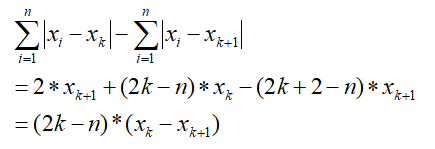
由于我们已经将n个点排序,所以 x k − x k + 1 x_k-x_{k+1} xk−xk+1始终小于等于0,当k小于等于n/2时,2k-n小于等于0,从而上式大于等于0;当k大于等于n/2时,2k-n大于等于0,从而上式小于等于0。这表明随着k逐渐增大,距离先变小再变大,在k=n/2时取得最小值。具体的,当n=2k为偶数时,上式在k和k+1位置处相等并取得最小值;当n=2k+1为奇数时,上式在k+1位置处取得最小值,此时即是中位数。将奇偶两种情况统一考虑,在k+1也即n/2+1位置处我们可以获得距离最小值。 - 假设使距离最小的点不是给定的n个点,则最优位置可以是数轴上的任意位置。很显然的,首先可以将n个数确定范围之外的区间都排除掉,也即最优点既不可能小于n个点中的最小值也不可能大于n个点中的最大值。这样剩余需要考虑的最优点就可能是n个点之间的小区间。我们研究一下曼哈顿距离在这段区间上的变化趋势。选择任意一段区间
x
k
<
c
1
<
c
2
<
x
k
+
1
x_k<c_1<c_2<x_{k+1}
xk<c1<c2<xk+1,重新计算
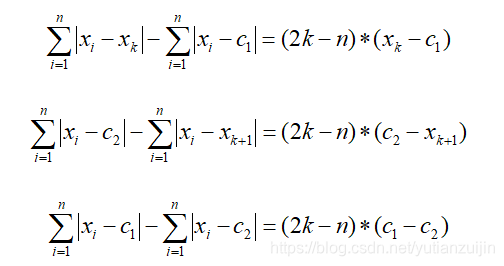
从上面的公式我们可以看出,当k小于等于n/2时,距离公式满足 d ( x k ) > d ( c 1 ) > d ( c 2 ) > d ( x k + 1 ) d(x_k)>d(c_1)>d(c_2)>d(x_{k+1}) d(xk)>d(c1)>d(c2)>d(xk+1),当k大于等于n/2时, d ( x k ) < d ( c 1 ) < d ( c 2 ) < d ( x k + 1 ) d(x_k)<d(c_1)<d(c_2)<d(x_{k+1}) d(xk)<d(c1)<d(c2)<d(xk+1)。也即在整个连续空间上距离先减后增。从而当n=2k为偶数时,区间 [ x n / 2 , x n / 2 + 1 ] [x_{n/2},x_{n/2+1}] [xn/2,xn/2+1]之间的任意数均可以取得最小值,当我们取 ( x n / 2 + x n / 2 + 1 ) / 2 (x_{n/2}+x_{n/2+1})/2 (xn/2+xn/2+1)/2时即表示中位数;当n=2k+1为奇数时,距离在k+1位置处取得最小值,此时还是中位数。
通过对离散和连续两种情况的考虑,我们可以得到结论:使上述公式取最小值的元素为中位数,不过我们可以统一选择排序之后的第n/2+1个元素,奇偶均如此。
最小化高维曼哈顿距离
由于在高维曼哈顿距离中只有加法操作,所以我们可以将每个维度分开考虑,在每个维度上分别按照一维的情况求排序后的第n/2+1个元素,然后组合起来即是最小化的高维曼哈顿距离。
最小化带权曼哈顿距离
有时我们还会遇到比上面更复杂的情况:每个点除了坐标
x
i
x_i
xi还都附带一个权重
w
i
w_i
wi,求使
∑
w
i
∣
x
i
−
a
∣
\sum{w_i|x_i-a|}
∑wi∣xi−a∣最小的点
a
a
a。在此我们也给出推导过程,看看使距离最小的点在什么位置。在上面的证明中我们分离散和连续两种情况考虑,在此我们直接考虑n个点确定的连续区间。假定给n个点已排序,给定点c满足
x
k
≤
c
<
x
k
+
1
x_k \leq c<x_{k+1}
xk≤c<xk+1我们求
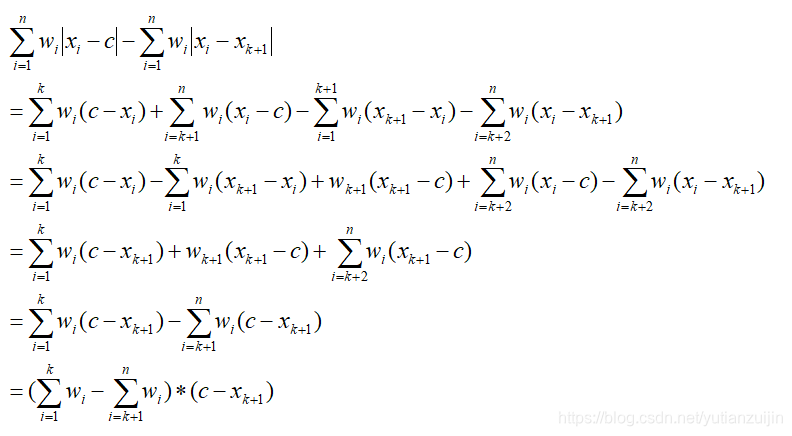
通过推导我们发现,影响距离变化的因素只是受制于权重,更确切地说是受制于前半部分权重和与后半部分权重和的差值。当
∑
i
=
1
k
w
i
<
∑
i
=
k
+
1
n
w
i
\displaystyle \sum^{k}_{i=1}{w_i}< \sum^{n}_{i=k+1}{w_i}
i=1∑kwi<i=k+1∑nwi时,
d
(
c
)
>
d
(
x
k
+
1
)
d(c)>d(x_{k+1})
d(c)>d(xk+1),此时距离在连续区间上逐渐变小;当
∑
i
=
1
k
w
i
>
∑
i
=
k
+
1
n
w
i
\displaystyle \sum^{k}_{i=1}{w_i}>\sum^{n}_{i=k+1}{w_i}
i=1∑kwi>i=k+1∑nwi时,
d
(
c
)
<
d
(
x
k
+
1
)
d(c)<d(x_{k+1})
d(c)<d(xk+1),距离在连续区间上又开始逐渐变大。所以使距离最小的位置k满足
∑
i
=
1
k
−
1
w
i
<
∑
i
=
k
n
w
i
\displaystyle \sum^{k-1}_{i=1}{w_i}< \sum^{n}_{i=k}{w_i}
i=1∑k−1wi<i=k∑nwi并且
∑
i
=
1
k
w
i
≥
∑
i
=
k
+
1
n
w
i
\displaystyle \sum^{k}_{i=1}{w_i} \geq \sum^{n}_{i=k+1}{w_i}
i=1∑kwi≥i=k+1∑nwi,含义就是前半部分权重和原本小于后半部分权重和,加上下一个位置的权重之后大小关系发生转变的位置。所以针对带权曼哈顿距离,我们需要做的就是将n个点排序,然后累加权重直到左侧权重大于右侧权重停止,此时就是使距离最小的位置。特别地,当n个点的权重均为正,且和为1时,分界点就是累加之后权重之和超过0.5的位置,这个位置被称为带权中位数(详细定义请参考算法导论)。
可以看出不管曼哈顿距离是否带权重,使距离最小的位置总是和中位数相关。希望上面的推导能有助于大家理解最小化曼哈顿距离。





















 652
652











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








