判断绝对收敛或条件收敛例题




绝对/条件收敛判定例题



对于比值判别法失效的场景,使用比较判别法

判断绝对收敛或条件收敛例题




绝对/条件收敛判定例题



交错级数

莱布尼兹判别法

莱布尼兹判别法证交错级数敛散性例题

第一型曲线积分

第二型曲线积分


曲线积分与路径相关的例子


格林公式的引入


平面曲线积分的路径无关的条件

单连通域与多(复)连通域

曲线积分路径无关例题
化简第二类曲线积分

不能应用路径无关&格林公式的例题

利用曲线积分性质的例题



二元函数的全微分与Ⅱ曲线积分


参考
回顾一般级数的敛散性证明(适用于正项级数)



补充
级数间 (比较判别法 [极限形式] )


单个级数前后一般项之间(达朗贝尔比值法)




达朗贝尔比值法的例题


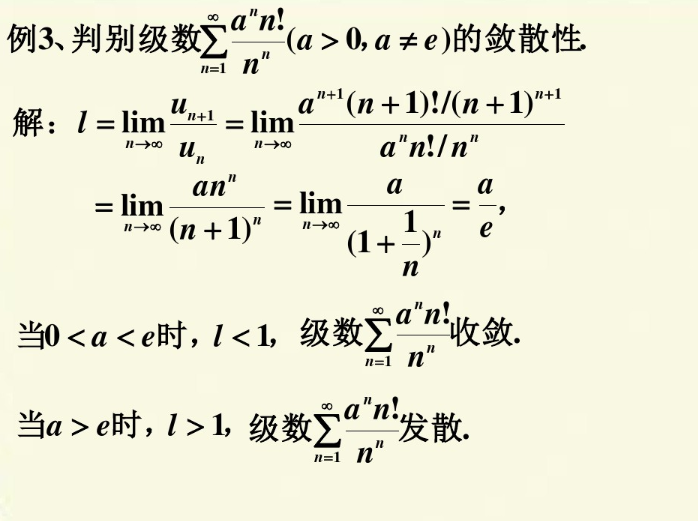
单个一般项(根值判别法)




根值判别法的例题


参考

收敛的意思








数项级数与数列的敛散性关系





更多例题







分割证例题

参考
公式

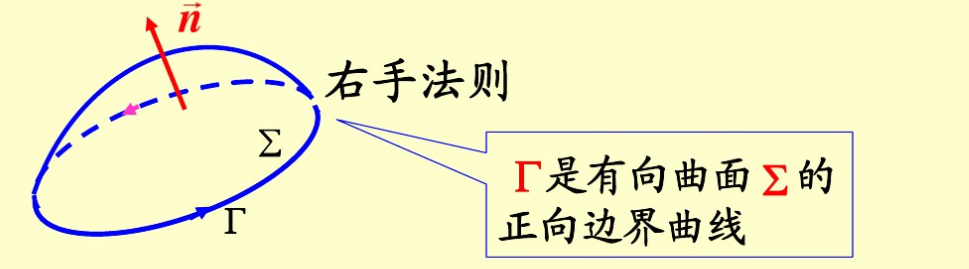
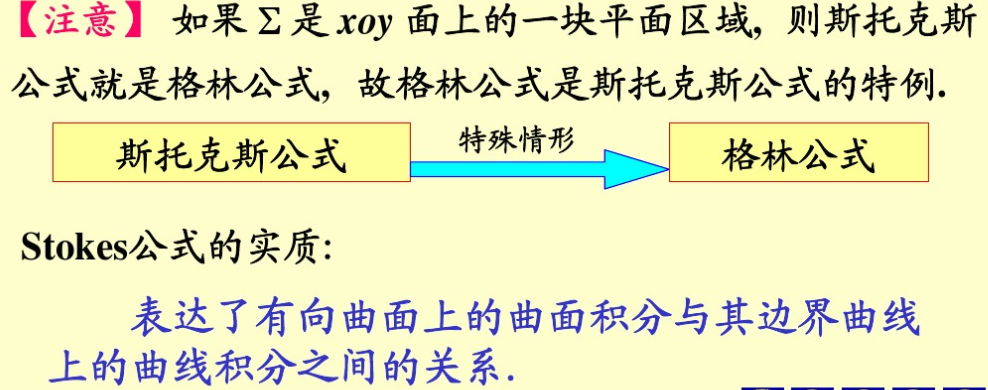
公式记忆

简单积分应用

物理应用
环流量与旋度






参考

高斯公式

高斯公式的证明


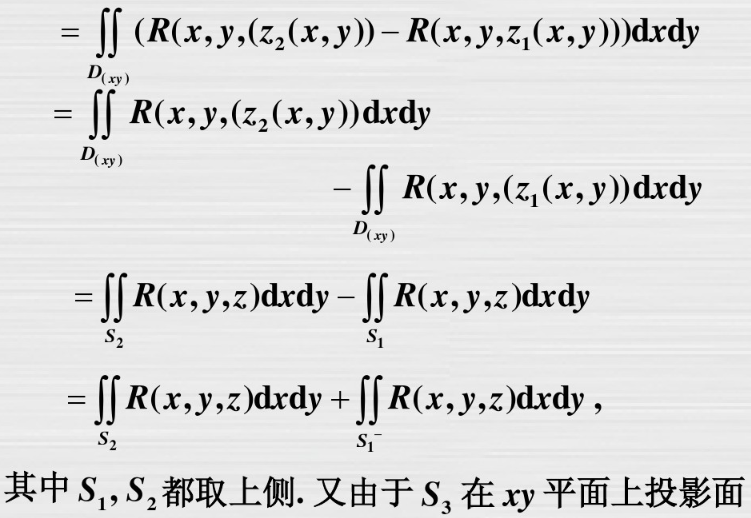

证明高斯定理



斯托克斯公式

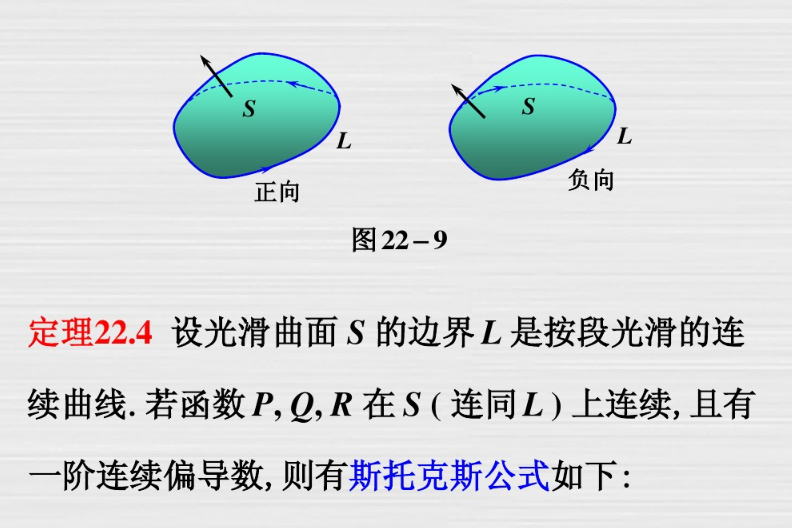


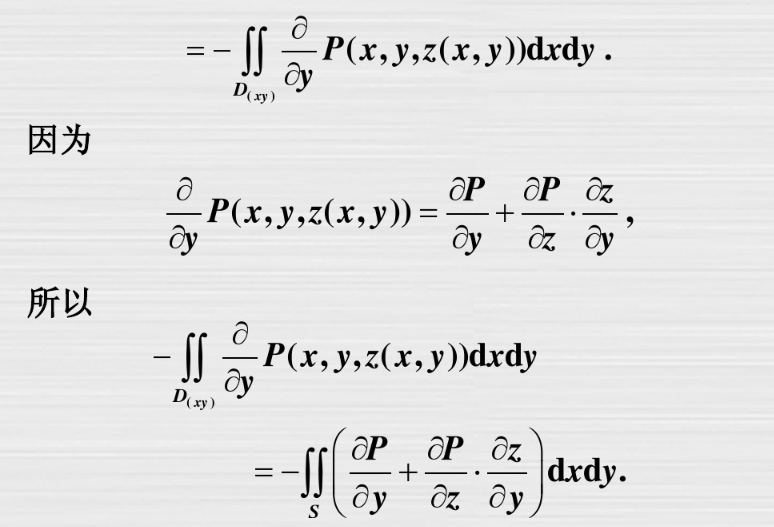
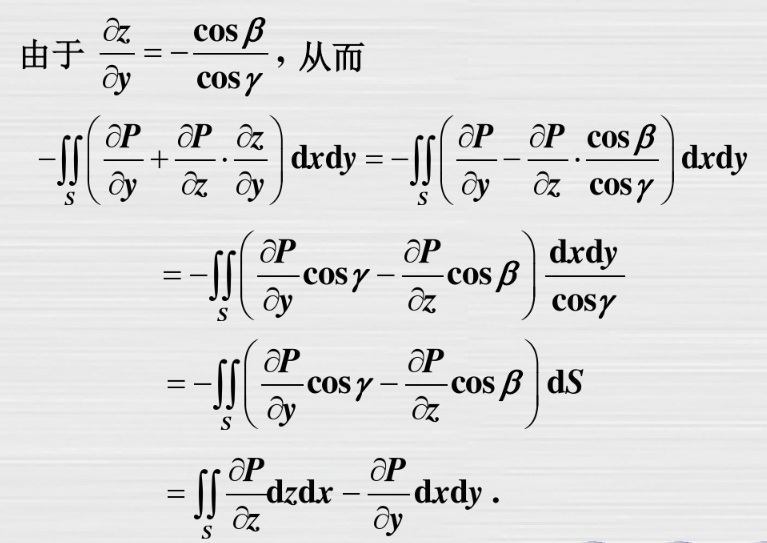


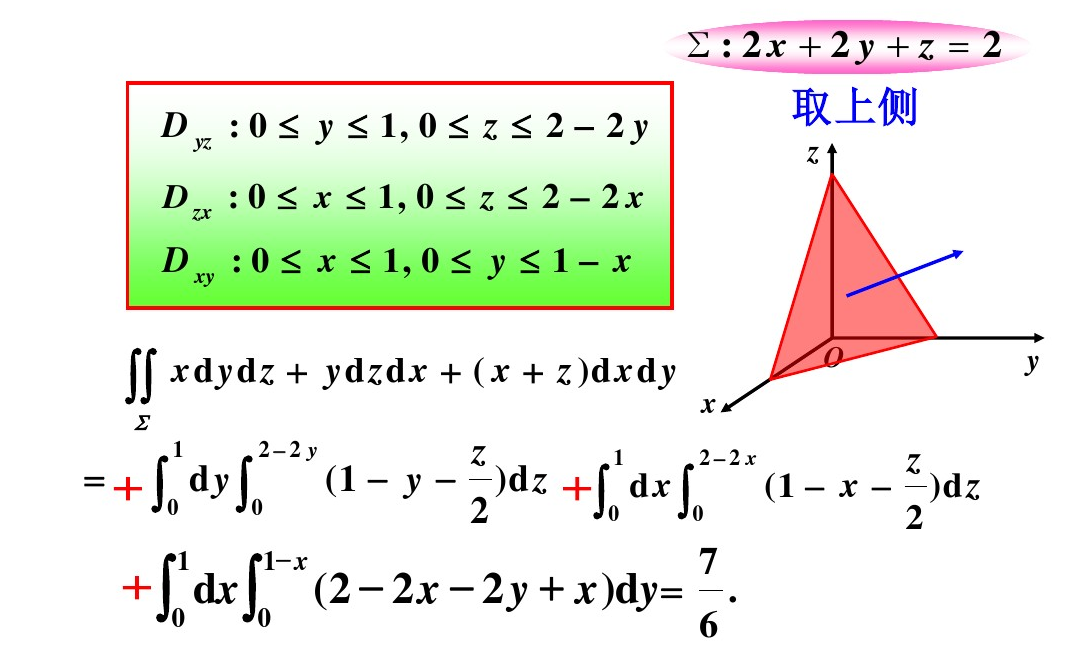
例题

区域V按曲面单连通

空间曲线积分的路径无关性


空间曲线积分与路径无关


参考
有向曲面
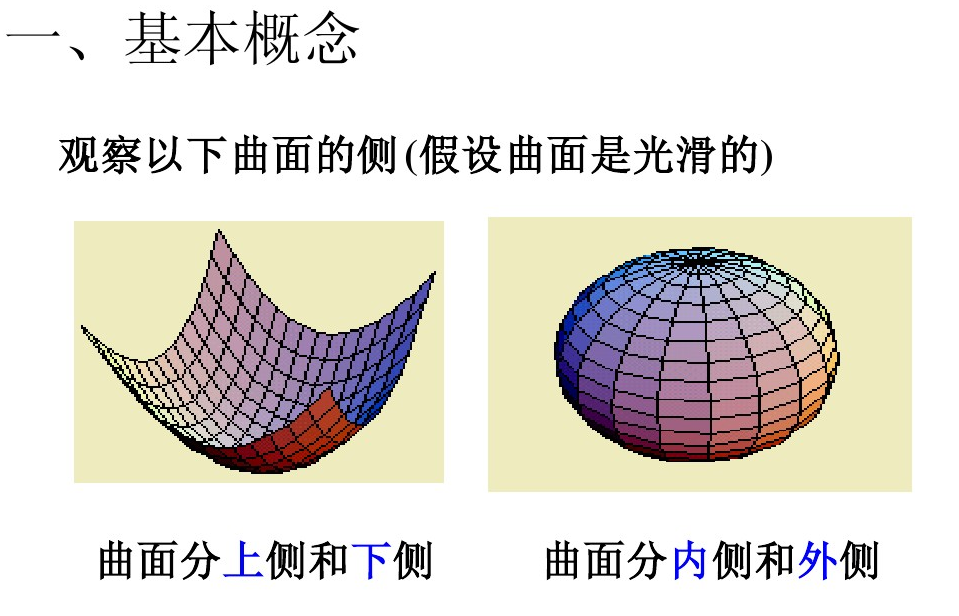
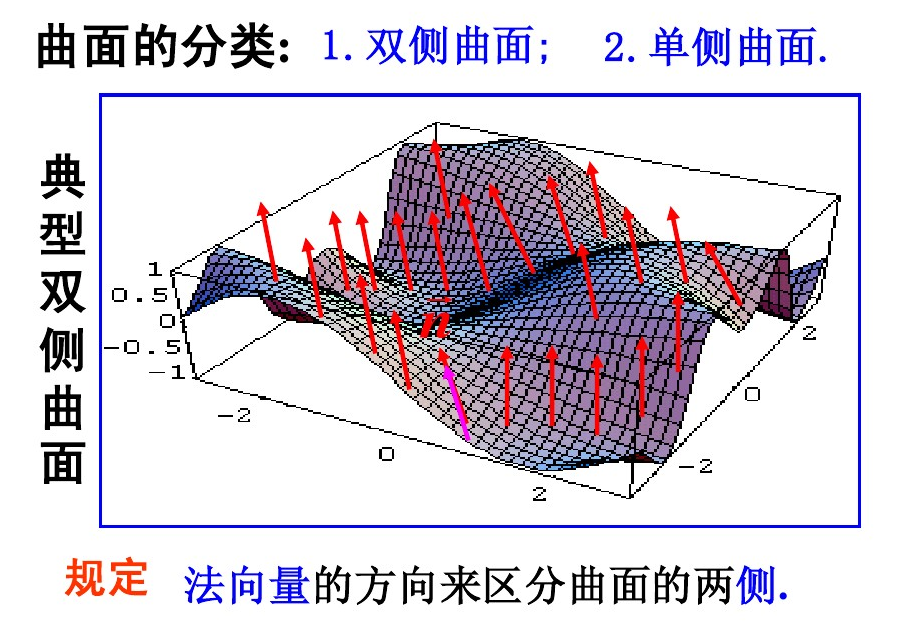
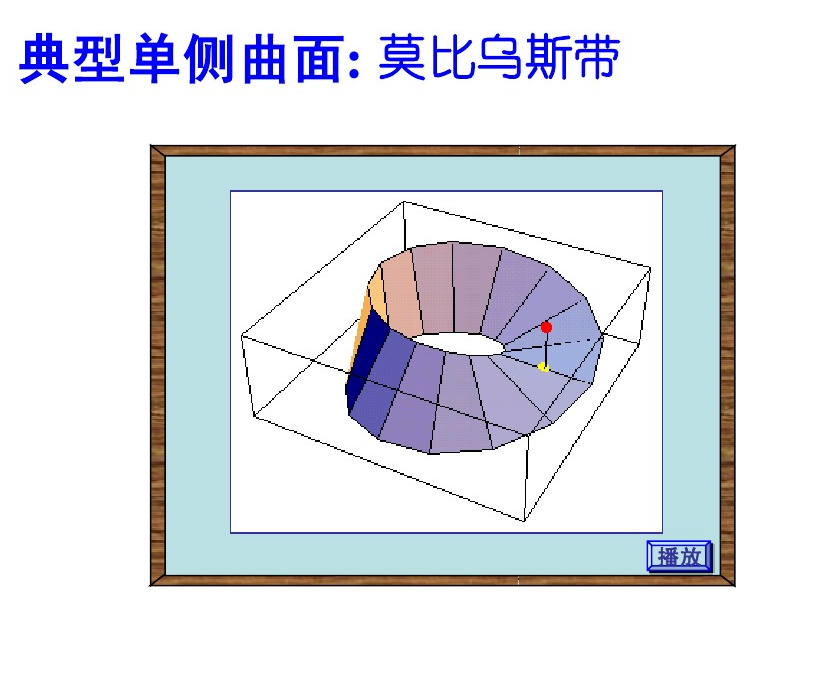
有向曲面和其投影曲面的表示


有向曲面与流量
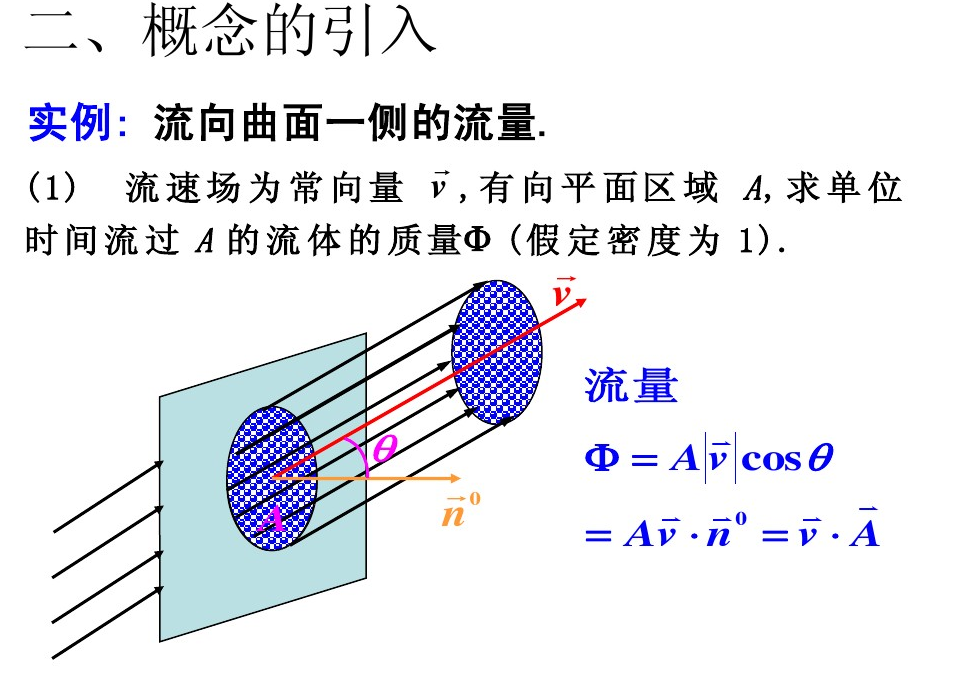
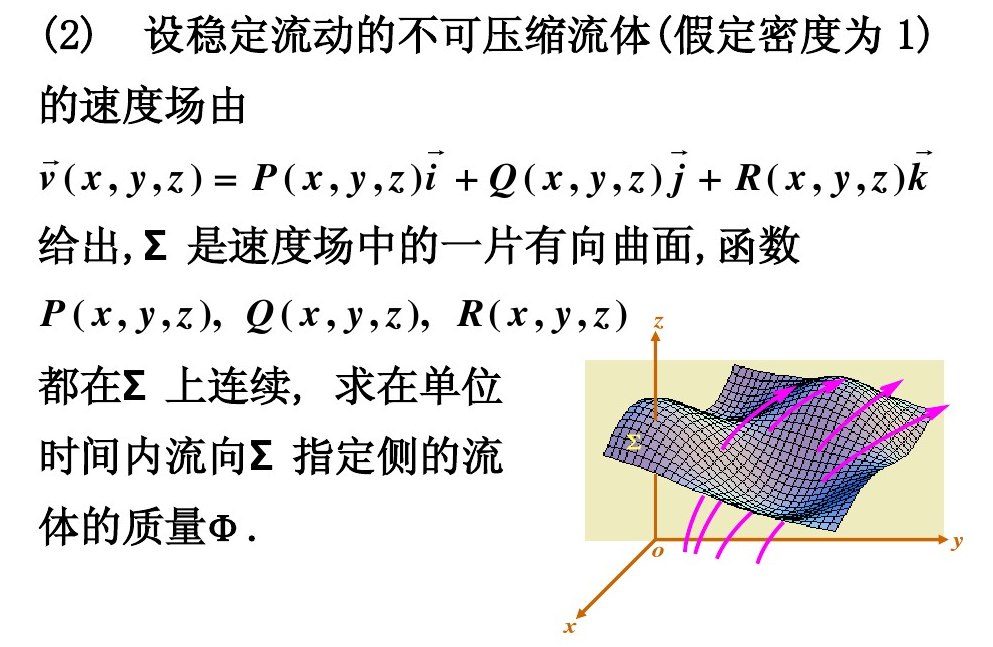
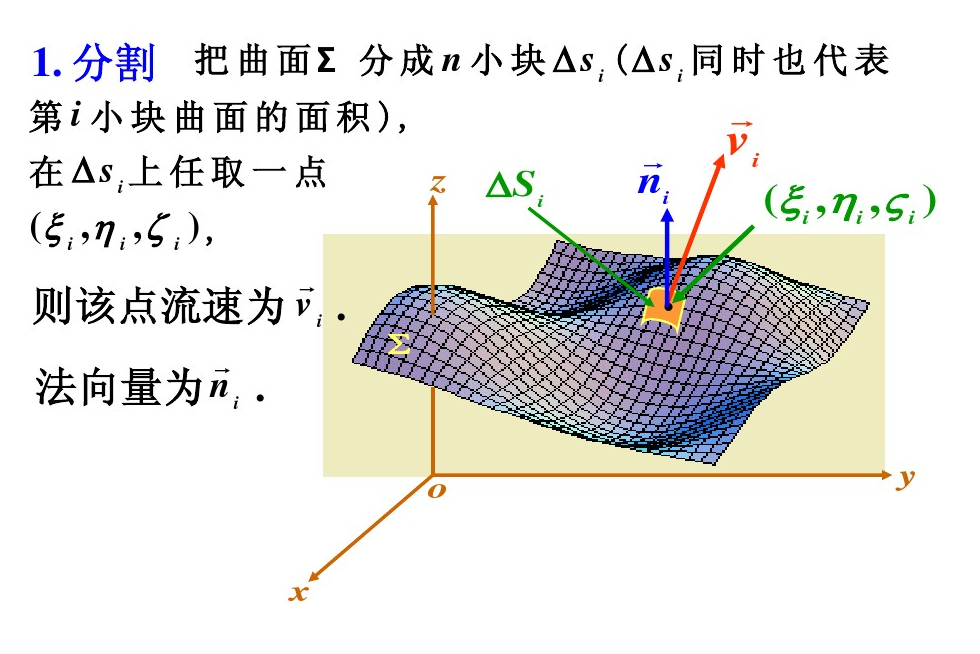


概念与性质


第二类曲面积分存在的条件

性质
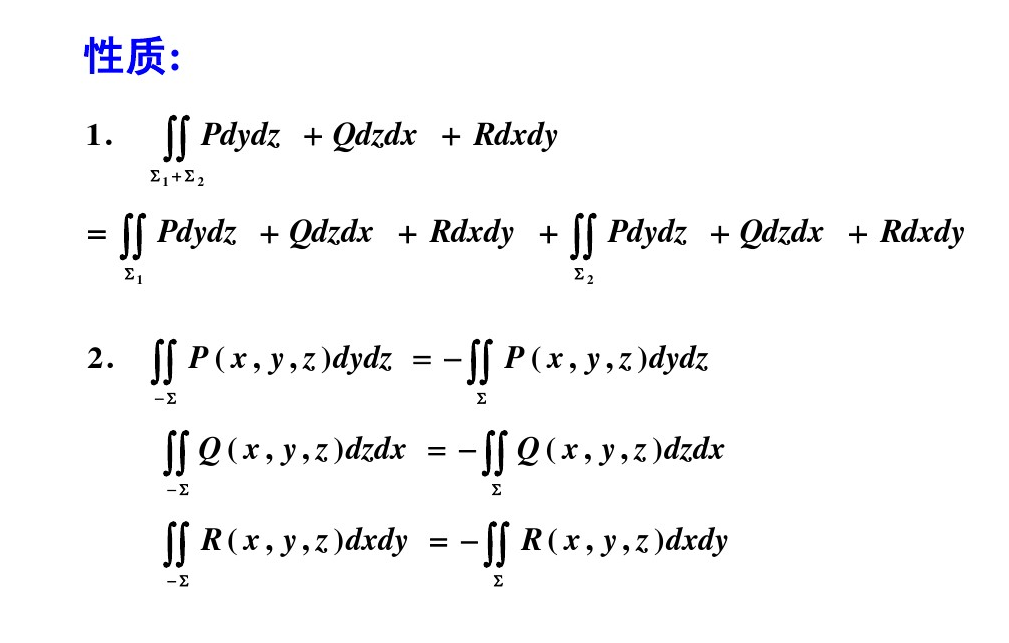
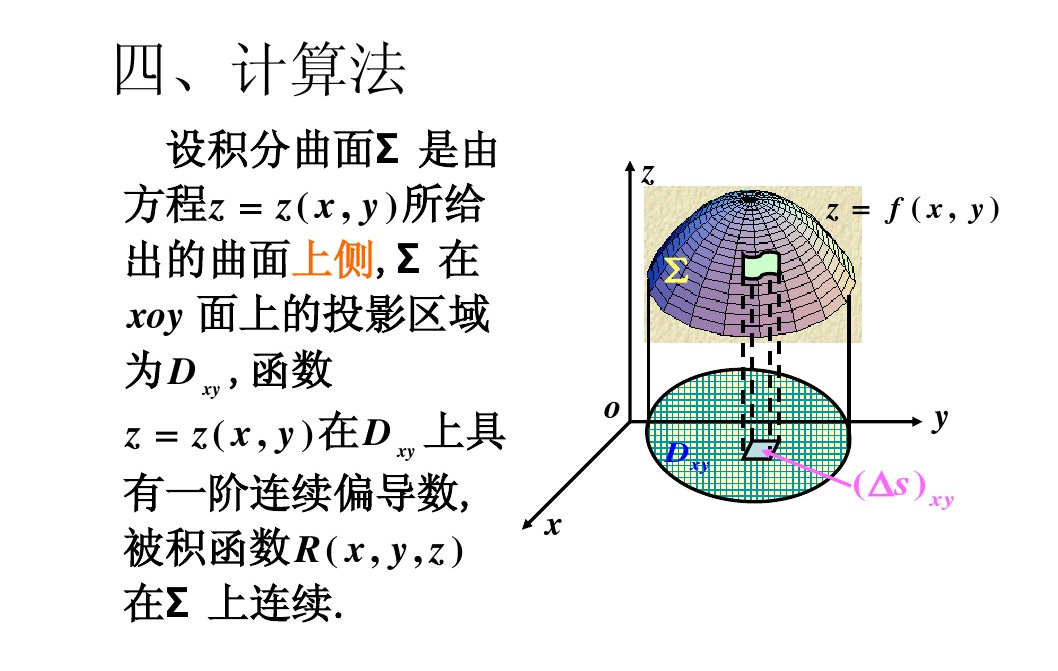
计算


例题



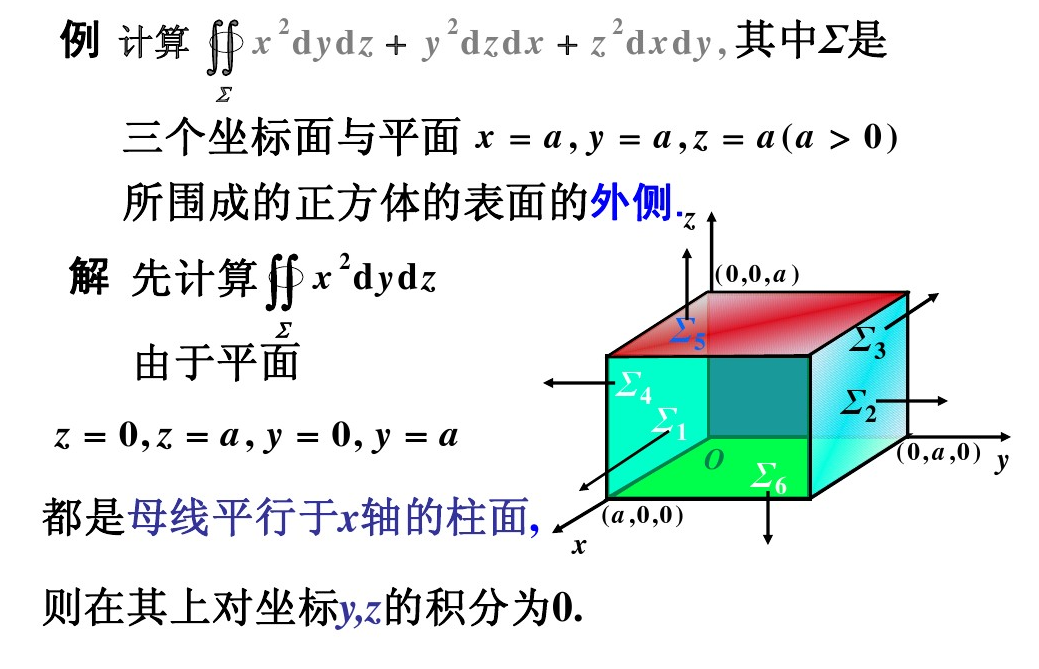
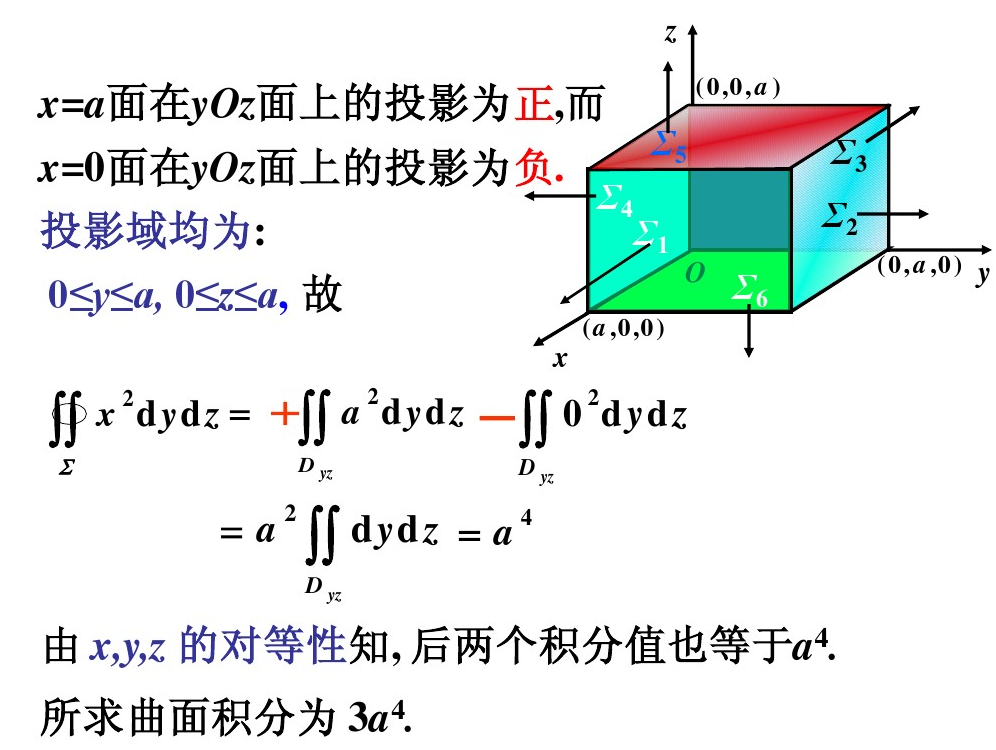
两类曲面积分联系

利用联系(合一投影法)计算