9.2: Efectos Cinemáticos Relativistas

Antes de proceder a otros corolarios de las ecuaciones (19), dediquemos unos minutos a discutir qué significan realmente estas relaciones. Evidentemente, están tratando de decirnos que los intervalos espaciales y temporales no son absolutos (como lo son en el espacio newtoniano), sino que sí dependen del marco de referencia en el que se midan. Entonces, tenemos que entender muy claramente qué es exactamente lo que se puede medir — y así se puede discutir en una teoría de la física significativa. Reconociendo esta necesidad, A. Einstein ha introducido la noción de numerosos observadores imaginarios que pueden distribuirse por todo el marco de referencia. Cada observador tiene un reloj y puede utilizarlo para medir los instantes de eventos locales, tomando toma en su ubicación. También conjeturó, muy razonablemente, que:

(i) todos los observadores dentro del mismo marco de referencia podrán acordar una medida de longitud común (“una escala”), es decir, en sus posiciones relativas en ese marco, y sincronizar sus relojes, ¹⁵ y

(ii) los observadores pertenecientes a diferentes marcos de referencia podrán acordar la nomenclatura de los eventos mundiales (por ejemplo, destellos cortos de luz) a los que se refieren sus respectivas mediciones.

En realidad, estos postulados adicionales ya han sido implícitos en nuestra “derivación” de la transformación de Lorentz en la Sec. 1. Por ejemplo, por el conjunto\(\ \{x, y, z, t\}\) nos referimos a los resultados de las mediciones de espacio y tiempo de un determinado evento mundial, al respecto que todos los observadores pertenecientes al fotograma 0 están de acuerdo. De igual manera, todos los observadores del marco 0' tienen que estar de acuerdo sobre los resultados\(\ \left\{x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime}\right\}\). Por último, cuando el origen del fotograma 0' pasa por algunos puntos secuenciales xk del fotograma 0, los observadores en ese fotograma pueden medir sus tiempos de paso\(\ t_{k}\) sin un error fundamental, y saber que todos estos tiempos pertenecen\(\ x^{\prime}=0\).

Ahora podemos analizar los principales corolarios de la transformación de Lorentz, que son bastante llamativos desde el punto de vista de nuestra experiencia cotidiana (más bien no relativista: -).

(i) Contracción de longitud. Consideremos una varilla delgada y rígida, posicionada a lo largo del eje\(\ x\)\(\ l \equiv x_2-x_1\), con su longitud, donde\(\ x_{1,2}\) están las coordenadas de los extremos de la varilla, medidas en su marco de reposo 0, en cualquier instante\(\ t\) (Fig. 4). ¿Cuál sería la longitud de la varilla\(\ l’\) medida por los observadores de Einstein en el marco móvil 0'?

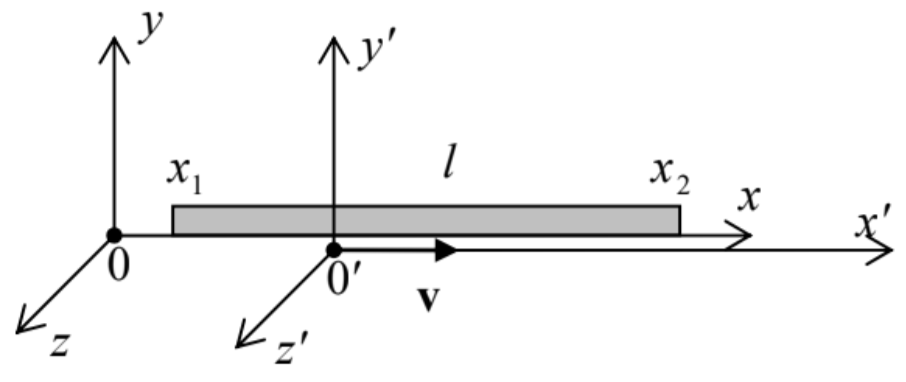Fig. 9.4. La contracción relativista de la longitud.

En un instante de tiempo\(\ t^{\prime}\) acordado de antemano, los observadores que se encuentren exactamente en los extremos de la varilla, pueden registrar ese hecho, y luego restar sus coordenadas\(\ x_{1,2}^{\prime}\) para calcular la longitud aparente de la varilla\(\ l^{\prime} \equiv x_{2}^{\prime}-x_{1}^{\prime}\) en el marco móvil. De acuerdo con la Ec. (19a),\(\ l\) puede expresarse a través de esto\(\ l^{\prime}\) como

\[\ l \equiv x_{2}-x_{1}=\gamma\left(x_{2}^{\prime}+\beta c t^{\prime}\right)-\gamma\left(x_{1}^{\prime}+\beta c t^{\prime}\right)=\gamma\left(x_{2}^{\prime}-x_{1}^{\prime}\right) \equiv \gamma l^{\prime}.\tag{9.20a}\]

Por lo tanto, la longitud de la varilla, medida en el marco de referencia móvil es

\[\ \text{Length contraction}\quad\quad\quad\quad l^{\prime}=\frac{l}{\gamma}=l\left(1-\frac{\nu^{2}}{c^{2}}\right)^{1 / 2} \leq l,\tag{9.20b}\]

de acuerdo con la hipótesis FitzGerald-Lorentz (5). Este es el efecto relativista de contracción de longitud: un objeto es siempre el más largo (tiene la llamada longitud adecuada\(\ l\)) si se mide en su marco de reposo.

Tenga en cuenta que de acuerdo con las ecuaciones (19), la contracción de longitud se produce solo en la dirección del movimiento relativo de dos marcos de referencia. Como se ha señalado en la Sec. 1, este resultado explica de inmediato el resultado cero de los experimentos tipo Michelson-Morley, de manera que dan pruebas muy convincentes (si no pruebas irrefutables) de las Ecuaciones (18) a (19).

(ii) Dilatación del tiempo. Ahora usemos las ecuaciones (19a) para encontrar el intervalo de tiempo\(\ \Delta t\), medido en algún marco de referencia 0, entre dos eventos mundiales —digamos, dos ticks de un reloj moviéndose con otro cuadro 0' (Fig. 5), es decir, que tiene valores constantes de\(\ x^{\prime}, y^{\prime}\), y\(\ z^{\prime}\).

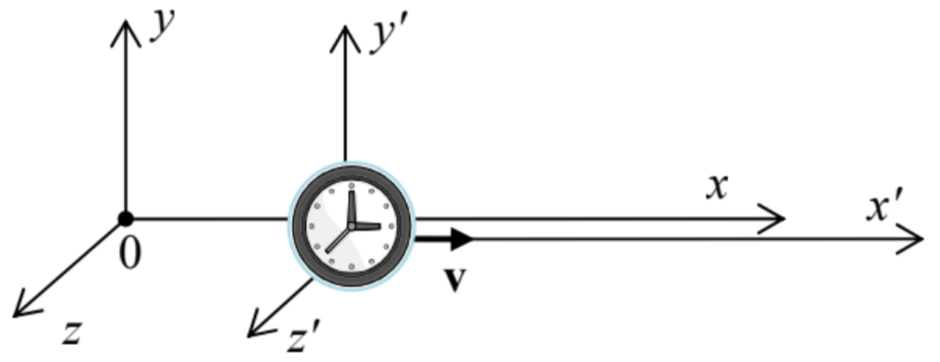Fig. 9.5. La dilatación relativista del tiempo.

Deje que el intervalo de tiempo entre estos dos eventos, medido en el cuadro de descanso del reloj 0', sea\(\ \Delta t^{\prime} \equiv t_{2}^{\prime}-t_1^{\prime}\). En estos dos momentos, el reloj volaría por ciertos dos observadores de Einstein en reposo en el fotograma 0, para que puedan registrar los momentos correspondientes\(\ t_{1,2}\) mostrados por sus relojes, y luego calcularlos\(\ \Delta t\) como su diferencia. Según la última de las ecuaciones (19a),

\[\ c \Delta t \equiv c t_{2}-c t_{1}=\gamma\left[\left(c t_{2}^{\prime}+\beta x^{\prime}\right)-\left(c t_{1}^{\prime}+\beta x^{\prime}\right)\right] \equiv \gamma c \Delta t^{\prime},\tag{9.21a}\]

para que, finalmente,

\[\ \Delta t=\gamma \Delta t^{\prime} \equiv \frac{\Delta t^{\prime}}{\left(1-\nu^{2} / c^{2}\right)^{1 / 2}} \geq \Delta t^{\prime}.\quad\quad\quad\quad\text{Time dilation}\tag{9.21b}\]

Este es el famoso efecto relativista de dilatación temporal (o “dilatación”): un intervalo de tiempo es más largo si se mide en un fotograma (en nuestro caso, el fotograma 0) que se mueve en relación con el reloj, mientras que en el fotograma de descanso del reloj es el más corto posible, el llamado intervalo de tiempo adecuado.

Este efecto contra-intuitivo es la realidad cotidiana en los experimentos con partículas elementales de alta energía. Por ejemplo, en un experimento típico (y de ninguna manera récord) realizado en Fermilab, un haz de 200 piones GeV cargados con\(\ \gamma \approx 1,400\) recorrió una distancia de\(\ l=300 \mathrm{~m}\) con la pérdida medida de solo 3% de la intensidad del haz inicial debido a la descomposición del pión (principalmente, en pares muón-neutrino) con el vida útil adecuada\(\ t_{0} \approx 2.56 \times 10^{-8} \mathrm{~s}\). Sin la dilatación temporal, solo sobreviviría una\(\ \exp \left\{-l / c t_{0}\right\} \sim 10^{-17}\) fracción de los piones iniciales, mientras que el número corregido por la relatividad\(\ \exp \{-l / c t\}=\exp \{-l/c\gamma t_0\}\approx0.97\), estuvo en total acuerdo con las mediciones experimentales.

Como otro ejemplo, los sistemas de posicionamiento global (digamos, el GPS) están diseñados con la cuenta de la dilatación del tiempo debido a la velocidad de sus satélites (y también algunas correcciones inducidas por la gravedad, es decir, la relatividad general, que no tendría tiempo de discutir) y darían grandes errores sin tales correcciones. Entonces, no cabe duda de que la dilatación temporal (21) es una realidad, aunque la precisión de sus pruebas experimentales que conozco de ¹⁶ se ha visto limitada en un poco por ciento, debido a la casi inevitable implicación de efectos de gravedad menos controlables —que proporcionan un cambio de intervalo de tiempo de la signo opuesto en la mayoría de los experimentos cerca de la superficie de la Tierra.

Antes de la primera observación confiable de la dilatación del tiempo (de B. Rossi y D. Hall en 1940), había habido serias dudas en la realidad de este efecto, siendo la más famosa la paradoja gemela planteada por primera vez (junto con una sugerencia inmediata de su resolución) por P. Langevin en 1911. Enviemos a uno de los dos gemelos a un largo viaje estelar con una velocidad que\(\ \nu\) se acerca\(\ c\). A su regreso a la Tierra, ¿quién de los gemelos sería mayor? El enfoque ingenuo es decir que debido al principio de relatividad, no se puede ser uno (y por lo tanto no hay dilatación de tiempo) porque cada gemelo podría afirmar que su contraparte más que ellos, se movía, con la misma velocidad pero en sentido contrario. La resolución de la paradoja en la teoría general de la relatividad (que puede manejar no sólo la gravedad, sino también los efectos de aceleración) es que uno de los gemelos tuvo que ser acelerado para ser devuelto, y de ahí que los marcos de referencia tengan que ser disímiles: sólo uno de ellos puede permanecer inercial todo el tiempo. Debido a eso, el gemelo que había sido acelerado (“en realidad viajando”) sería más joven que su hermano cuando finalmente se junten.

(iii) Transformación de velocidad. Ahora calculemos la velocidad\(\ \mathbf{u}\) de una partícula, como se observa en el marco de referencia 0, siempre que su velocidad, medida en el cuadro 0', sea\(\ \mathbf{u}^{\prime}\) (Fig. 6).

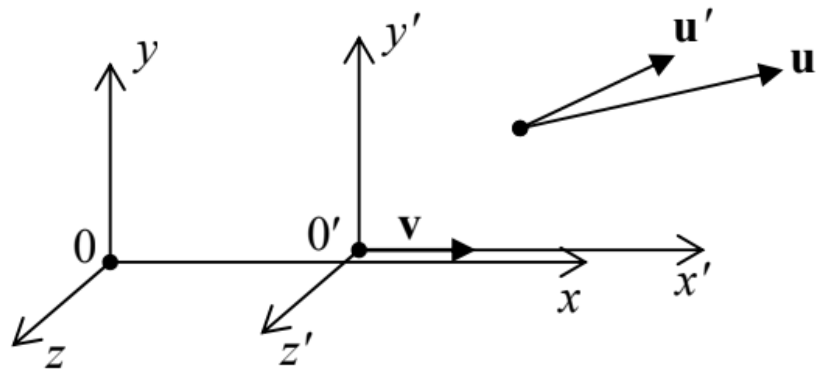Fig. 9.6. La adición de velocidad relativista.

Manteniendo la definición habitual de velocidad, pero con la debida atención a la relatividad no solo de los intervalos espaciales sino también temporales, podemos escribir

\[\ \mathbf{u} \equiv \frac{d \mathbf{r}}{d t}, \quad \mathbf{u}^{\prime} \equiv \frac{d \mathbf{r}^{\prime}}{d t^{\prime}}.\tag{9.22}\]

Conectando los diferenciales de las relaciones de transformación de Lorentz (6a) en estas definiciones, obtenemos

\[\ u_{x} \equiv \frac{d x}{d t}=\frac{d x^{\prime}+\nu d t^{\prime}}{d t^{\prime}+\nu d x^{\prime} / c^{2}} \equiv \frac{u_{x}^{\prime}+\nu}{1+u_{x}^{\prime} \nu / c^{2}}, \quad u_{y} \equiv \frac{d y}{d t}=\frac{1}{\gamma} \frac{d y^{\prime}}{d t^{\prime}+\nu d x^{\prime} / c^{2}} \equiv \frac{1}{\gamma} \frac{u_{y}^{\prime}}{1+u_{x}^{\prime} \nu / c^{2}},\tag{9.23}\]

y una fórmula similar para\(\ u_{z}\). En el límite clásico\(\ \nu / c \rightarrow 0\), estas relaciones se reducen a

\[\ u_{x}=u_{x}^{\prime}+\nu, \quad u_{y}=u_{y}^{\prime}, \quad u_{z}=u_{z}^{\prime},\tag{9.24a}\]

y puede fusionarse en la forma galilea familiar

\[\ \mathbf{u}=\mathbf{u}^{\prime}+\mathbf{v}, \quad \text { for } \nu<<c.\tag{9.24b}\]

Para ver cuán inusuales están en las reglas relativistas completas (23)\(\ u \sim c\), consideremos primero un movimiento puramente longitudinal,\(\ u_{y}=u_{z}=0\) luego ¹⁷

\[\ u=\frac{u^{\prime}+\nu}{1+u^{\prime} \nu / c^{2}},\quad\quad\quad\quad\text{Longitudinal velocity addition}\tag{9.25}\]

dónde\(\ u \equiv u_{x}\) y\(\ u^{\prime} \equiv u_{x}^{\prime}\). La Figura 7 muestra\(\ u\) como función\(\ u^{\prime}\) dada por esta fórmula, para varios valores de la velocidad relativa de los marcos de referencia\(\ \nu\).

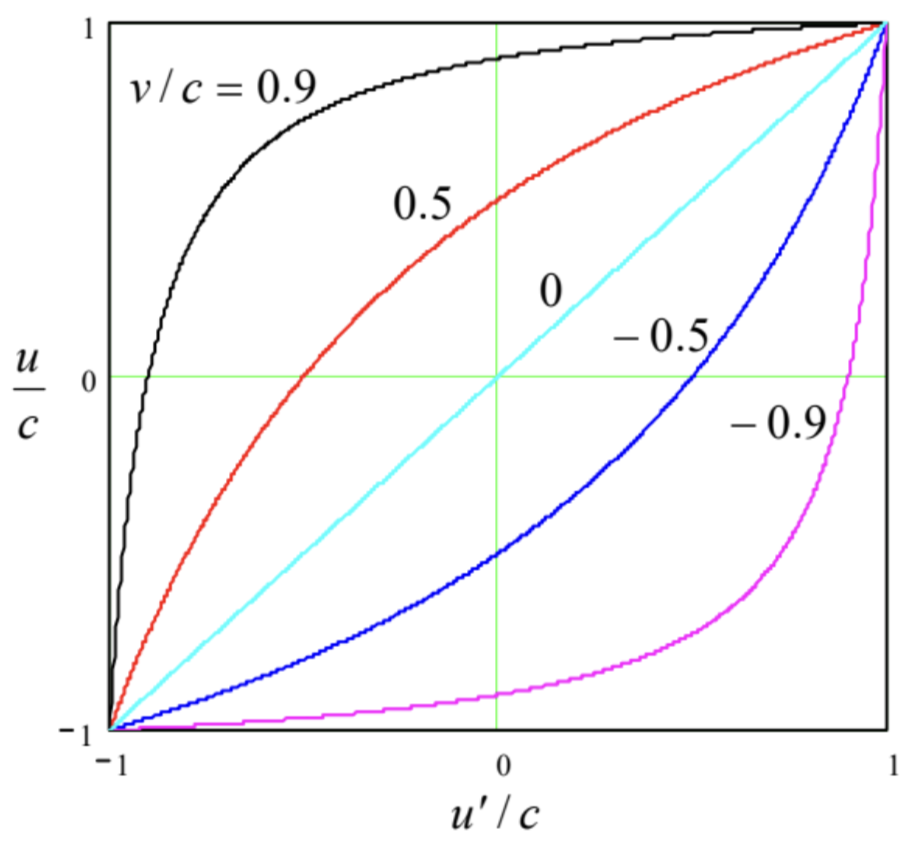Fig. 9.7. La adición de velocidades longitudinales.

La primera comprobación de cordura es que si\(\ \nu=0\), es decir, los marcos de referencia están en reposo uno relativo al otro\(\ u=u^{\prime}\), entonces, como debería ser — vea la línea recta diagonal en la Fig. 7. A continuación, si las magnitudes de\(\ u^{\prime}\) y\(\ \nu\) están ambas por debajo\(\ c\), también lo es la magnitud de\(\ u\). (También es bueno, porque de lo contrario las partículas ordinarias en un cuadro serían taquiones en el otro, y la teoría estaría en grandes problemas). Ahora empiezan cosas extrañas: aun cuando\(\ u^{\prime}\) y ambos\(\ \nu\) se acercan\(\ c\), entonces también\(\ u\) está cerca de\(\ c\), pero no lo supera. Como ejemplo, si disparamos hacia adelante una bala con la velocidad relativa\(\ 0.9 c\), desde una nave espacial que se mueve desde la Tierra también a\(\ 0.9 c\), la ecuación (25) predice que la velocidad de la bala en relación con la Tierra es justa\(\ [(0.9+0.9) /(1+0.9 \times 0.9)] c \approx 0.994c<c\), en lugar de\(\ (0.9+0.9) c=1.8 c>c\) como en la cinemática galilea. En realidad, podríamos esperar esta extrañeza, porque es necesario cumplir con el ^segundo postulado de Einstein: la independencia de la velocidad de la luz en cualquier marco de referencia. En efecto, para\(\ u^{\prime}=\pm c\), Eq. (25) rinde\(\ u=\pm c\), independientemente de\(\ \nu\).

En el caso contrario de un movimiento puramente transversal, cuando una partícula se mueve a través del movimiento relativo de los fotogramas (por ejemplo, a nuestra elección de coordenadas\(\ u_{x}^{\prime}=u_{z}^{\prime}=0\),, Ecuaciones (23) producen un resultado mucho menos espectacular

\[\ u_{y}=\frac{u_{y}^{\prime}}{\gamma} \leq u_{y}^{\prime}.\tag{9.26}\]

Este efecto proviene puramente de la dilatación del tiempo porque las coordenadas transversales son invariantes de Lorentz.

En el caso cuando ambos\(\ u_{x}^{\prime}\) y\(\ u_{y}^{\prime}\) son sustanciales (pero\(\ u_{z}^{\prime}\) sigue siendo cero), podemos dividir las ecuaciones (23) entre sí para relacionar los ángulos\(\ \theta\) de propagación de las partículas, como se observa en los dos marcos de referencia:

\[\ \tan \theta \equiv \frac{u_{y}}{u_{x}}=\frac{u_{y}^{\prime}}{\gamma\left(u_{x}^{\prime}+\nu\right)}=\frac{\sin \theta^{\prime}}{\gamma\left(\cos \theta^{\prime}+\nu / u^{\prime}\right)}\quad\quad\quad\quad\text{Stellar aberration effect}\tag{9.27}\]

Esta expresión describe, en particular, el llamado efecto de aberración estelar: la dependencia de la dirección observada\(\ \theta\) hacia una estrella de la velocidad v del movimiento del telescopio en relación con la estrella — ver Fig. 8. (El efecto es fácilmente observable experimentalmente como la aberración anual debida al cambio periódico de velocidad\(\ \nu\) por\(\ 2 \nu_{\mathrm{E}} \approx 60 \mathrm{~km} / \mathrm{s}\) causa de la rotación de la Tierra alrededor del Sol. Dado que la parte principal de la aberración es de primer orden en\(\ \nu_{\mathrm{E}} / c \sim 10^{-4}\), este efecto es muy significativo y se conoce desde principios de 1700.)

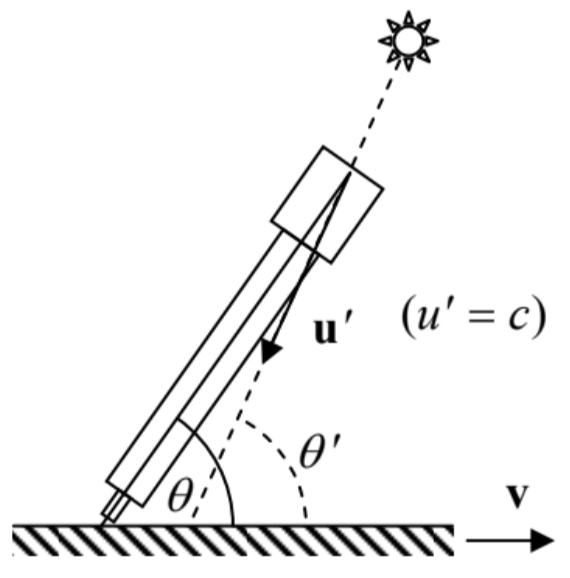Fig. 9.8. La aberración estelar.

Para el análisis de este efecto, es suficiente tomar, en la Ec. (27)\(\ u^{\prime}=c\), es decir\(\ \nu / u^{\prime}=\beta\), e interpretar\(\ \theta^{\prime}\) como la dirección “apropiada” a la estrella, que se mediría en\(\ \nu=0\). ¹⁸ At\(\ \beta<<1\), tanto la Ec. (27) como el resultado galileano (que se invita al lector a derivar directamente de la Fig. 8),

\[\ \tan \theta=\frac{\sin \theta^{\prime}}{\cos \theta^{\prime}+\beta}\tag{9.28}\]

puede ser bien aproximado por el término de primer orden

\[\ \Delta \theta \equiv \theta-\theta^{\prime} \approx-\beta \sin \theta^{\prime}.\tag{9.29}\]

Desafortunadamente, no es fácil usar la diferencia entre las ecuaciones (27) y (28), de segundo orden en\(\ \beta\), para la confirmación especial de la relatividad, porque otros componentes del movimiento de la Tierra, como su rotación, nutación y precesión inducida por par, ¹⁹ dan enmascaramiento contribuciones de primer orden a la aberración.

Finalmente, para una dirección completamente arbitraria del vector\(\ \mathbf{u}^{\prime}\), las ecuaciones (22) pueden usarse fácilmente para calcular la magnitud de la velocidad. La forma más popular de la expresión resultante es para el cuadrado de la velocidad relativa (o más bien la velocidad relativa reducida\(\ \boldsymbol{\beta}\)) de dos partículas,

\[\ \beta^{2}=\frac{\left(\boldsymbol{\beta}_{1}-\boldsymbol{\beta}_{2}\right)^{2}-\left|\boldsymbol{\beta}_{1} \cdot \boldsymbol{\beta}_{2}\right|}{\left(1-\boldsymbol{\beta}_{1} \cdot \boldsymbol{\beta}_{2}\right)^{2}} \leq 1.\tag{9.30}\]

donde\(\ \boldsymbol{\beta}_{1,2} \equiv \mathbf{v}_{1,2} / c\) están sus velocidades normalizadas medidas en el mismo marco de referencia.

(iv) El efecto Doppler. Consideremos una onda plana monocromática que se mueve a lo largo del eje x:

\[\ f=\operatorname{Re}\left[f_{\omega} \exp \{i(k x-\omega t\}] \equiv\left|f_{\omega}\right| \cos \left(k x-\omega t+\arg f_{\omega}\right) \equiv\left|f_{\omega}\right| \cos \Psi\right..\tag{9.31}\]

Su fase total,\(\ \Psi \equiv k x-\omega t+\arg f_{\omega}\) (en contraste con su amplitud\(\ \left|f_{\omega}\right|\) - ver Sec. 5) no puede depender del marco de referencia del observador, porque todos los campos de la onda desaparecen simultáneamente en\(\ \Psi=\pi(n+1 / 2)\) (para todos los enteros\(\ n\)), y tales “eventos mundiales” deben ser observables en todos los marcos de referencia. La única manera de mantener\(\ \Psi=\Psi^{\prime}\) en todo momento es tener ²⁰

\[\ k x-\omega t=k^{\prime} x^{\prime}-\omega^{\prime} t^{\prime}.\tag{9.32}\]

Primero, utilicemos esta relación general para considerar el efecto Doppler en ondas no relativistas habituales, por ejemplo, oscilaciones de partículas de cierto medio. Usando la transformada galileana (2), podemos reescribir la Eq. (32) como

\[\ k\left(x^{\prime}+\nu t\right)-\omega t=k^{\prime} x^{\prime}-\omega^{\prime} t.\tag{9.32}\]

Dado que esta transformación deja intactos todos los intervalos espaciales (incluida la longitud de onda\(\ \lambda=2 \pi / k\)), podemos tomar\(\ k=k^{\prime}\), de modo que la ecuación (33) rinde

\[\ \omega^{\prime}=\omega-k \nu.\tag{9.34}\]

Para un medio libre de dispersión, el número de onda\(\ k\) es la relación de su frecuencia\(\ \omega\), medida en el marco de referencia unido al medio, y la velocidad de onda\(\ \nu_{\mathrm{w}}\). En particular, si la fuente de onda descansa en el medio, también podemos unir el marco de referencia 0 al medio, y el fotograma 0' al receptor de la onda (es decir\(\ \nu=\nu_{\mathrm{r}}\)), de modo que

\[\ k=\frac{\omega}{\nu_{\mathrm{w}}},\tag{9.35}\]

y para la frecuencia percibida por el receptor, la Ec. (34) rinde

\[\ \omega^{\prime}=\omega \frac{\nu_{\mathrm{w}}-\nu_{\mathrm{r}}}{\nu_{\mathrm{w}}}.\tag{9.36}\]

Por otro lado, si el receptor y el medio están en reposo en el marco de referencia 0', mientras que la fuente de onda está ligada a la trama 0 (de manera que\(\ \nu=-\nu_{\mathrm{S}}\)), la Ec. (35) debe ser reemplazada por

\[\ k=k^{\prime}=\frac{\omega^{\prime}}{\nu_{\mathrm{w}}},\tag{9.37}\]

y la Eq. (34) produce un resultado diferente:

\[\ \omega^{\prime}=\omega \frac{\nu_{\mathrm{w}}}{\nu_{\mathrm{w}}-\nu_{\mathrm{s}}},\tag{9.38}\]

Finalmente, si tanto la fuente como el detector se mueven, es sencillo combinar estos dos resultados para obtener la relación general

\[\ \omega^{\prime}=\omega \frac{\nu_{\mathrm{w}}-\nu_{\mathrm{r}}}{\nu_{\mathrm{w}}-\nu_{\mathrm{s}}}.\tag{9.39}\]

A bajas velocidades tanto de la fuente como del receptor, este resultado simplifica,

\[\ \omega^{\prime} \approx \omega(1-\beta), \quad \text { with } \beta \equiv \frac{\nu_{\mathrm{r}}-\nu_{\mathrm{s}}}{\nu_{\mathrm{w}}},\tag{9.40}\]

pero a velocidades comparables a las que\(\ \nu_{\mathrm{w}}\) tenemos que usar la ecuación más general (39). Así, el efecto Doppler habitual generalmente se ve afectado no sólo por la velocidad relativa\(\ \left(\nu_{\mathrm{r}}-\nu_{\mathrm{s}}\right)\) de la fuente y el detector de la onda sino también por sus velocidades relativas al medio en el que se propagan las ondas.

Algo contraintuitivamente, para las ondas electromagnéticas los cálculos son más sencillos porque para ellas no existe el medio de propagación (aether), la velocidad de onda es igual\(\ \pm c\) en cualquier marco de referencia, y no hay dos casos separados: siempre podemos tomar\(\ k=\pm \omega / c\) y\(\ k^{\prime}=\pm \omega^{\prime} / c\). Conectando estas relaciones, junto con la transformada de Lorentz (19a), en la condición de invarianza de fase (32), obtenemos

\[\ \pm \frac{\omega}{c} \gamma\left(x^{\prime}+\beta c t^{\prime}\right)-\omega \gamma \frac{c t^{\prime}+\beta x^{\prime}}{c}=\pm \frac{\omega^{\prime}}{c} x^{\prime}-\omega^{\prime} t^{\prime}.\tag{9.41}\]

Esta relación tiene que mantenerse para cualquier\(\ x^{\prime}\) y\(\ t^{\prime}\), por lo que podemos requerir que los coeficientes netos antes de que estas variables desaparezcan. Estos dos requisitos producen la misma igualdad:

\[\ \omega^{\prime}=\omega \gamma(1 \mp \beta).\tag{9.42}\]

Este resultado ya es bastante simple, pero puede transformarse aún más para ser aún más esclarecedor:

\[\ \omega^{\prime}=\omega \frac{1 \mp \beta}{\left(1-\beta^{2}\right)^{1 / 2}} \equiv \omega\left[\frac{(1 \mp \beta)(1 \mp \beta)}{(1+\beta)(1-\beta)}\right]^{1 / 2}.\tag{9.43}\]

En cualquier signo anterior\(\ \beta\), se cancela un par de paréntesis, de manera que ²¹

\[\ \text{Longitudinal Doppler effect}\quad\quad\quad\quad \omega^{\prime}=\omega\left(\frac{1 \mp \beta}{1 \pm \beta}\right)^{1 / 2}.\tag{9.44}\]

Por lo tanto, el efecto Doppler para las ondas electromagnéticas depende únicamente de la velocidad relativa\(\ \nu=\beta c\) entre la fuente de onda y el detector, como debería ser, dada la ausencia del éter. A velocidades muy por debajo de c, la ecuación (44) puede aproximarse como

\[\ \omega^{\prime} \approx \omega \frac{1 \mp \beta / 2}{1 \pm \beta / 2} \approx \omega(1 \mp \beta),\tag{9.45}\]

es decir, en la primera aproximación en\(\ \beta \equiv \nu / c\) ella tiende al límite correspondiente (40) del efecto Doppler habitual.

Si el vector de onda k se inclina en ángulo con respecto\(\ \theta\) al vector v (como se mide en el fotograma 0), entonces tenemos que repetir los cálculos, con\(\ k\) reemplazados por\(\ k_{x}\), y componentes\(\ k_{y}\) y\(\ k_{z}\) dejados intactos en la transformada de Lorentz. Como resultado, la Ec. (42) se generaliza como

\[\ \omega^{\prime}=\omega \gamma(1-\beta \cos \theta).\tag{9.46}\]

Para los casos\(\ \cos \theta=\pm 1\), la ecuación (46) se reduce a nuestro resultado anterior (42). Sin embargo, en\(\ \theta=\pi / 2\) (i.e.\(\ \cos \theta=0\)), la relación es bastante diferente:

\[\ \omega^{\prime}=\gamma \omega \equiv \frac{\omega}{\left(1-\beta^{2}\right)^{1 / 2}}.\quad\quad\quad\quad \text{Transverse Doppler effect}\tag{9.47}\]

Se trata del efecto Doppler transversal —que está ausente en la física no relativista. Su primera evidencia experimental se obtuvo utilizando haces de electrones (como lo había sugerido en 1906 J. Stark), por H. Ives y G. Stilwell en 1938 y 1941. Posteriormente, experimentos similares se repitieron varias veces, pero las primeras mediciones inequívocas fueron realizadas solo en 1979 por D. Hasselkamp et al. quienes confirmaron la Ec. (47) con una precisión relativa de aproximadamente 10%. Esta precisión puede no parecer demasiado espectacular, pero además de las pruebas especiales discutidas anteriormente, las fórmulas de transformación de Lorentz también han sido confirmadas, de manera menos directa, por un enorme cuerpo de otros datos experimentales, especialmente en física de alta energía, coincidiendo con los cálculos que incorporan esta transformación como su parte. Por eso, con el debido respeto al espíritu de desafiar a la autoridad, debo advertir al lector: si decides desafiar la teoría de la relatividad (llamada “teoría” solo por tradición), también tendrías que explicar todos estos datos. ¡La mejor suerte con eso! ²²