2.5: Orbitales Hidrogénicos

La\(\Phi\) Ecuación

La\(\Phi\) ecuación resultante dice (el “símbolo se usa para representar la segunda derivada)

\[\Phi'' + m^2\Phi = 0.\]

Esta ecuación debería ser familiar porque es la ecuación que tratamos mucho antes cuando discutimos el componente z del momento angular. Entonces, su análisis posterior también debería ser familiar, pero para ser completo, repito gran parte de ello. La ecuación anterior tiene como su solución más general

\[ \Phi = A e^{im\phi} + B e^{-im\phi} .\]

Debido a que las funciones de onda de la mecánica cuántica representan densidades de probabilidad, deben ser continuas y de un solo valor. Esta última condición, aplicada a nuestra\(\Phi\) función, significa (n.b., lo usamos en nuestra discusión anterior del componente z del momento angular) que

\[\Phi(\phi) = \Phi(2\pi+\phi) \]

o

\[Ae^{im\phi}(1-e^{2im\pi})+ Be^{-im\phi}(1-e^{2im\pi})​= 0.\]

Esta condición se satisface solo cuando la constante de separación es igual a un entero\(m = 0, ±1, ± 2, \cdots \). Esto proporciona otro ejemplo de la regla de que la cuantificación proviene de las condiciones de límite en la función de onda. Aquí\(m\) se restringe a ciertos valores discretos porque la función de onda debe ser tal que cuando rotas\(2\pi\) alrededor del eje z, debes recuperar con lo que empezaste.

La\(\Theta\) Ecuación

Ahora volviendo a la ecuación en la que la\(\phi\) dependencia se aisló de la\(r\) y\(\theta\) dependencia y reordenando los\(\theta\) términos hacia el lado izquierdo, tenemos

\[ \frac{1}{\sin\theta}\frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial Q}{\partial\theta} \right) - \frac{m^2Q}{\sin^2\theta} = F(r)Q.\]

En esta ecuación hemos separado los\(r\) términos\(\theta\) y, por lo que podemos descomponer aún más la función de onda introduciendo\(Q = \Theta(\theta) R(r)\), que rinde

\[\frac{1}{\Theta\sin\theta}\frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial \Theta}{\partial\theta} \right) - \frac{m^2}{\sin^2\theta} = \frac{F(r)Q}{R}=-\lambda.\]

donde se ha introducido una segunda constante de separación\(-\lambda\),, una vez que los términos\(r\) y\(\theta\) dependientes se han separado en los lados derecho e izquierdo, respectivamente.
Ahora podemos escribir la\(\theta\) ecuación como
\[ \frac{1}{\sin\theta}\frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial \Theta}{\partial\theta} \right) - \frac{m^2\Theta}{\sin^2\theta} = -\lambda\Theta.\]
donde\(m\) está el entero introducido anteriormente. Para resolver esta ecuación para\(\Theta\), hacemos las sustituciones\(z =\cos\theta\) y\(P(z) = \Theta(\theta)\), entonces\(\sqrt{1-z^2}=\sin\theta\), y
\[ \frac{\partial }{\partial \theta} = \frac{\partial z}{\partial \theta}\frac{\partial }{\partial z}= - \sin\theta ​\frac{\partial }{\partial z}.\]

El rango de valores para\(\theta\) fue\(0 \le \theta < \pi\), por lo que el rango para\(z\) es\(-1 < z < 1\). La ecuación para\(\Theta\), cuando se expresa en términos de\(P\) y\(z\), se convierte en

\[ \frac{d}{dz}\left((1-z^2)\frac{dP}{dz}\right)- \frac{m^2P}{1-z^2}+ \lambda P= 0.\]

Ahora podemos buscar soluciones polinómicas para\(P\), porque\(z\) se restringe a ser menor que la unidad en magnitud. Si\(m\) = 0, primero dejamos

\[ P= \sum_{k=0}a_kz^k,\]

y sustituir en la ecuación diferencial para obtener

\[ \sum_{k=0}(k+2)(k+1)a_{k+2}z^k - \sum_{k=0}(k+1)ka_{k}z^k+ \lambda\sum_{k=0}a_kz^k = 0.\]

Equiparar como poderes de\(z\) da

\[ a_{k+2} = \frac{a_k(k(k+1)-\lambda)}{(k+2)(k+1)}.\]

Tenga en cuenta que para grandes valores de\(k\)

\[\frac{a_{k+2}}{a_{k}} \rightarrow \frac{k^2\left(1+\frac{1}{k}\right)}{k^2\left(1+\frac{2}{k}\right)\left(1+\frac{1}{k}\right)} = 1.\]

Dado que los coeficientes no disminuyen con\(k\) para grandes\(k\), esta serie divergirá para\(z = ± 1\) a menos que se trunca en orden finito. Este truncamiento sólo ocurre si la constante de separación\(\lambda\) obedece\(\lambda = \lambda(\lambda+1)\), donde\(l\) es un entero (se puede ver esto a partir de la relación de recursión dando\(a_{k+2}\) en términos de\(a_k\); sólo para ciertos valores de\(l\) desaparecerá el numerador). Entonces, una vez más, vemos que una condición límite (es decir, que la función de onda no diverja y así sea normalizable en este caso) da lugar a la cuantificación. En este caso, los valores de\(l\) están restringidos a\(\lambda(\lambda+1)\); antes, vimos que\(m\) se restringe a\(0, ±1, ± 2, \cdots \).
Dado que la relación de recursión anterior vincula cada otro coeficiente, podemos elegir resolver para las funciones par e impar por separado. Elegir\(a_0\) y luego determinar todos los pares\(a_k\) en términos de esto\(a_1\), seguido de reescalar todos estos\(a_k\) para normalizar la función genera una solución pareja. Elegir\(a_1\) y determinar todo lo impar\(a_k\) de la misma manera, genera una solución impar.
Para\(l= 0\), la serie trunca después de un término y da como resultado\(P_o(z) = 1\). Por\(l= 1\) lo mismo aplica y\(P_1(z) = z\). Para\(l= 2\),\(a_2 = -6 \dfrac{a_o}{2}= -3a_o\), así se obtiene\(P_2 = 3z^2-1\), y así sucesivamente. Estos polinomios se denominan polinomios de Legendre y se denotan\(P_l(z)\).
Para el caso más general donde\(m \ne 0\), se puede proceder como antes para generar una solución polinómica para la\(Q\) función. Al hacerlo, se obtienen las siguientes soluciones:
\[P_l^m(z)=(1-z^2)^{|m|/2}\frac{d^{|m|}P_l(z)}{dz^{|m|}}\]
Estas funciones se denominan polinomios de Legendre Asociados, y constituyen las soluciones al\(Q\) problema para\(m\) valores distintos de cero.
Lo anterior\(P\) y\(e^{im\phi}\) las funciones, cuando se reexpresan en términos de\(\theta\) y\(\phi\), producen la parte angular completa de la función de onda para cualquier potencial centrosimétrico. Estas soluciones suelen escribirse como

\[Y_{l,m}(\theta,\phi)= P_l^m(\cos\theta)\frac{1}{\sqrt{2\pi}} \exp(im\phi),\]

y se llaman armónicos esféricos. Proporcionan la solución angular de la ecuación de\(r,\theta,\phi\) Schrödinger para cualquier problema en el que el potencial dependa únicamente de la coordenada radial. Tales situaciones incluyen todos los átomos e iones de un electrón (por ejemplo\(H\)\(He^+\),,\(Li^{2+}\),, etc.), el movimiento de rotación de una molécula diatómica (donde el potencial depende solo de la longitud del enlace\(r\)), el movimiento de un nucleón en una caja esféricamente simétrica (como ocurre en el modelo de concha de núcleos), y la dispersión de dos átomos (donde el potencial depende únicamente de la distancia interatómica).
Las\(Y_{l,m}\) funciones poseen un número variable de nodos angulares, que, como se señaló anteriormente, dan firmas claras del contenido de energía angular o rotacional de la función de onda. Estos nodos angulares se originan en la naturaleza oscilatoria de los polinomios Legendre y asociados de Legendre\(P_{lm}(\cos\theta)\); cuanto más alto\(l\) es, más cambios de signos ocurren dentro del polinomio.

La\(R\) Ecuación

Ahora volvamos nuestra atención a la ecuación radial, que es el único lugar donde aparece la forma explícita del potencial. Usando nuestros resultados anteriores para la ecuación obedecida por la\(R(r)\) función y especificando\(V(r)\) que es el potencial Coulomb apropiado para un electrón en el campo de un núcleo de carga\(+Z_e\), produce:

\[\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left(\frac{2\mu}{\hbar^2}\left(E+\frac{Ze^2}{r}\right)-\frac{L(L+1)}{rZ2}\right) R = 0.\]

Podemos simplificar las cosas considerablemente si elegimos unidades de longitud y energía reescaladas porque al hacerlo se eliminan los factores que dependen de\(\mu\),\(\hbar\), y\(e\). Introducimos una nueva coordenada radial\(\rho\) y\(a\) cantidad de\(\sigma\) la siguiente manera:

\[\rho=r\sqrt{\frac{-8\mu E}{\hbar^2}} \text{ and } \sigma = \frac{\mu Ze^2}{\hbar\sqrt{-2\mu E}}.\]

Observe que si\(E\) es negativo, como lo será para estados ligados (es decir, aquellos estados con energía por debajo de la de un electrón libre infinitamente lejos del núcleo y con cero energía cinética),\(\rho\) y\(\sigma\) son reales. Por otro lado, si\(E\) es positivo, como lo será para estados que se encuentran en el continuum,\(\rho\) y\(\sigma\) serán imaginarios. Estos dos casos darán lugar a comportamientos cualitativamente diferentes en las soluciones de la ecuación radial que se desarrollan a continuación.

Ahora definimos una función\(S\) tal que\(S(\rho) = R(r)\) y sustituimos\(S\)\(R\) para obtener:

\[\frac{1}{\rho^2}\frac{d}{d\rho}\left(\rho^2\frac{dS}{d\rho}\right) + \left(-\frac{1}{4}-\frac{L(L+1)}{\rho^2}+\dfrac{\sigma}{\rho}\right) S = 0.\]

Los términos del operador diferencial se pueden refundir de varias maneras usando

\[\frac{1}{\rho^2}\frac{d}{d\rho}\left(\rho^2\frac{dS}{d\rho}\right)=\frac{d^2 S}{d\rho^2} +\frac{2}{\rho}\frac{dS}{d\rho} =\frac{1}{\rho}\frac{d^2}{d\rho^2}(\rho S) .\]

La estrategia que ahora seguimos es característica de resolver ecuaciones diferenciales de segundo orden. Examinaremos la ecuación para\(S\)\(\rho\) valores grandes y pequeños. Habiendo encontrado soluciones en estos límites, utilizaremos una serie de potencias\(\rho\) para interpolar entre estos dos límites.

Comencemos por examinar la solución de la ecuación anterior a valores pequeños de\(\rho\) para ver cómo se comportan las funciones radiales en pequeño\(\rho\). As\(\rho\rightarrow0\), el término\(-\dfrac{L(L+1)}{\rho^2}\) dominará sobre\(-\dfrac{1}{4} +\dfrac{\sigma}{\rho}\). Despreciando estos otros dos términos, encontramos que, para valores pequeños de\(\rho\) (o\(r\)), la solución debe comportarse como\(\rho^L\) y porque la función debe ser normalizable, debemos tener\(L \ge 0\). Dado que\(l\) puede ser cualquier entero no negativo, esto sugiere la siguiente forma más general para\(S(r)\):
\[ S(\rho) \approx \rho^L e^{-a\rho}.\]
Esta forma asegurará que la función sea normalizable ya que\(S(r) \rightarrow 0\) como\(r \rightarrow \infty\) para todos\(L\), como siempre y cuando\(\rho\) sea una cantidad real. Si\(\rho\) es imaginario, tal forma puede no ser normalizada (ver más abajo para más consecuencias).
Pasando ahora al comportamiento de\(S\) para grande\(\rho\), hacemos la sustitución de\(S(r)\) en la ecuación anterior y mantenemos solo los términos con mayor potencia de\(\rho\) (es decir, el\(-1/4\) término) y permitimos las derivadas en el diferencial anterior ecuación sobre la que actuar\(\approx \rho^L e^{-a\rho}​\). Al hacerlo, obtenemos la ecuación
\[ a^2\rho^Le^{-a\rho} = \frac{1}{4}\rho^Le^{-a\rho}​ ,\]
que nos lleva a concluir que el exponente en el\(r\) comportamiento grande de S es\(a = \dfrac{1}{2}\).
Habiendo encontrado los\(\rho\) comportamientos pequeños\(\rho\) y grandes de\(S(\rho)\), podemos tomar\(S\) para tener la siguiente forma para interpolar entre los valores r grandes y pequeños:
\[S(\rho) = \rho^L​e^{-\frac{\rho}{2}}​​P(\rho),\]
donde la función \(P\)se expande en una serie de potencias infinitas en\(\rho\) as\(P(\rho) =\sum a_k\rho^k\). Nuevamente sustituyendo esta expresión por\(S\) en la ecuación anterior obtenemos
\[P"\rho + P'(2L+2-\rho) + P(\sigma-L-l) = 0,\]
y luego sustituyendo la expansión de la serie de potencia\(P\) y resolviendo por los ak, llegamos a una relación de recursión para los coeficientes ak :
\[a_{k+1} = \frac{(k-\sigma+L+1)a_k}{(k+1)(k+2L+2)}.\]
Para grandes\(k\), la relación de coeficientes de expansión alcanza el límite\(\dfrac{a_{k+1}}{a_k}=\dfrac{1}{k}\), que, cuando se sustituye en\(\sum a_k\rho^k\), da el mismo comportamiento que la expansión de la serie de potencia de\(e^\rho\). Debido a que la expansión de la serie de potencias de\(P\) describe una función que se comporta como\(e^\rho\) para grandes\(\rho\), la\(S(\rho)\) función resultante no sería normalizable porque el efactor se vería abrumado por esta\(e^\rho\) dependencia. De ahí que la expansión en serie del\(P\) must truncate para lograr una\(S\) función normalizable. Observe que si\(\rho\) es imaginario, como lo será si\(E\) está en el continuum, ya no se aplica el argumento de que la serie debe truncar para evitar una función exponencialmente divergente. Así, vemos una diferencia clave entre los estados ligados (con\(\rho\) reales) y continuum (con r imaginarios). En el primer caso, surge la condición límite de no divergencia; en el segundo, no lo hace porque\(e^{\frac{\rho}{2}}\) no diverge si\(\rho\) es imaginario.

Para truncar en un polinomio de orden\(n'\), debemos tener\(n'-s+L+l= 0\). Esto implica que la cantidad s introducida anteriormente está restringida a\(s = n'+L+l\), que sin duda es un entero; llamemos a este entero\(n\). Si etiquetamos estados en orden de incremento\(n = 1,2,3,\cdots \), vemos que hacerlo es consistente con especificar un orden máximo (\(n'\)) en el\(P(r)\) polinomio\(n' = 0,1,2,\cdots \) después del cual el\(\textbf{L}_{-}\) valor puede correr desde\(L = 0\), en pasos de unidad hasta\(L = n-1\).

Sustituyendo el entero\(n\) por\(s\), encontramos que los niveles de energía se cuantifican porque\(s\) se cuantifica (igual a\(n\)):

\[E = -\frac{\mu Z^2 e^4}{2\hbar^2 n^2}\]

y la distancia escalada resulta ser

\[\rho = \frac{Zr}{a_0n}.\]

Aquí, la longitud\(a_o=\dfrac{\hbar^2}{\mu e^2}\) es el llamado radio de Bohr, que resulta ser 0.529 Å; aparece una vez que la expresión E anterior se sustituye en la ecuación para\(\rho\). El uso de la ecuación de recursión para resolver los coeficientes del polinomio\(a_k\) para cualquier elección de\(n\) y números\(L\) cuánticos genera un llamado polinomio de Laguerre;\(P_{n-L-1}(\rho)\). Contienen potencias\(\rho\) de cero a través\(n-L-1\), y tienen cambios de\(n-L-1\) signo a medida que la coordenada radial va de cero a infinito. Son estos cambios de signo en los polinomios de Laguerre los que hacen que las partes radiales de las funciones de onda hidrogénica tengan\(n-L-1\) nodos. Por ejemplo,\(3d\) los orbitales no tienen nodos radiales, pero los orbitales 4d tienen uno; y, como se muestra en la Figura 2.16,\(3p\) los orbitales tienen uno mientras que\(3s\) los orbitales tienen dos. Una vez más, cuanto mayor sea el número de nodos, mayor será la energía en la dirección radial.

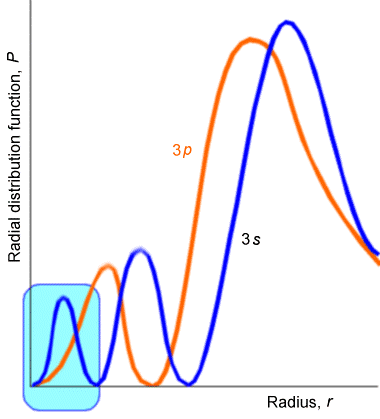
Permítanme recordarles nuevamente sobre el peligro de tratar de entender las funciones o probabilidades de onda cuántica en términos de dinámica clásica. ¿Qué tipo de potencial\(V(r)\) daría lugar, por ejemplo, a la\(3s\)\(P(r)\) trama mostrada arriba? La mecánica clásica sugiere que\(P\) debe ser grande donde la partícula se mueve lentamente y pequeña donde se mueve rápidamente. Entonces, la\(3s\)\(P(r)\) gráfica sugiere que la velocidad radial del electrón tiene tres regiones donde es baja (es decir, donde\(P\) están los picos en) y dos regiones donde es muy grande (es decir, donde están los nodos). Esto, a su vez, sugiere que el potencial radial\(V(r)\) experimentado por el\(3s\) electrón es alto en tres regiones (cerca de picos en P) y bajo en dos regiones. Por supuesto, esta conclusión sobre la forma de\(V(r)\) es absurda y de nuevo ilustra cómo no se debe atraer a tratar de pensar en el movimiento clásico de la partícula, especialmente para estados cuánticos con pequeño número cuántico. De hecho, los estados de número cuántico bajo de tales átomos e iones de un electrón tienen sus\(P(r)\) gráficas radiales enfocadas en regiones del espacio r donde el potencial\(–Ze^2/r\) es más atractivo (es decir, mayor en magnitud).

Por último, observamos que la cuantificación de energía no surge para los estados que se encuentran en el continuum debido a que la condición de que la expansión de\(P(r)\) terminar no surge. Las soluciones de la ecuación radial apropiadas a estos estados de dispersión (que se relacionan con el movimiento de dispersión de un electrón en el campo de un núcleo de carga\(Z\)) están un poco fuera del alcance de este texto, por lo que no las trataremos más aquí.

Para revisar, se ha utilizado la separación de variables para resolver la ecuación completa de\(r,\theta,\phi\) Schrödinger para un electrón que se mueve alrededor de un núcleo de carga\(Z\). Las\(\phi\) soluciones\(\theta\) y son los armónicos esféricos\(Y_{L,m} (\theta,\phi)\). Las soluciones radiales de estado límite

\[R_{n,L}(r) = S(\rho) = \rho^Le^{-\frac{\rho}{2}}P_{n-L-1}(\rho)\]

dependen de los números\(n\) y\(L\) cuánticos y se dan en términos de los polinomios de Laguerre.

Resumen

Para resumir, los números cuánticos\(L\) y\(m\) surgen a través de condiciones límite que requieren que\(\psi(\theta)\) sean normalizables (es decir, no divergir) y\(\psi(\phi) = \psi(\phi+2\pi)\). Se encuentra que la ecuación radial, que es el único lugar donde entra la energía potencial, posee tanto estados límite (es decir, estados cuyas energías se encuentran debajo de la asíntota en la que el potencial desaparece y la energía cinética es cero) como estados continuos que se encuentran energéticamente por encima de esta asíntota. Los primeros estados están espacialmente confinados por el potencial, pero los segundos no lo son. Las funciones de onda hidrogénicas resultantes (angular y radial) y las energías se resumen en las pp. 133-136 en el texto de L. Pauling y E. B. Wilson para\(n\) hasta e incluyendo 6 y\(L\) hasta 5 (es decir, para\(s, p, d, f, g,\) y\(h\) orbitales).

Hay soluciones tanto ligadas como continuas a la ecuación radial de Schrödinger para el atractivo potencial culombo porque, a energías por debajo de la asíntota, el potencial limita la partícula entre\(r=0\) y un punto de inflexión clásico externo, mientras que en energías por encima de la asíntota, la partícula no es más tiempo confinado por un punto de inflexión exterior (ver Figura 2.17). Esto proporciona otro ejemplo más de cómo surgen los estados cuantificados cuando el potencial limita espacialmente la partícula, pero los estados de continuo surgen cuando la partícula no está confinada espacialmente.

Figura 2.17: Potencial radial para átomos hidrogénicos y energías orbitales unidas y continuas.

Las soluciones de este problema de un electrón forman la base cualitativa de gran parte de la teoría orbital atómica y molecular. Por esta razón, se alienta al lector a obtener una comprensión más firme de la naturaleza de las partes radial y angular de estas funciones de onda. Los orbitales que resultan están etiquetados por\(n\)\(l\), y números\(m\) cuánticos para los estados unidos y por\(l\) y números\(m\) cuánticos y la energía\(E\) para los estados continuos. Por mucho que los orbitales de partículas en una caja se utilizan para describir cualitativamente electrones p en polienos conjugados, estos llamados orbitales similares a hidrógeno proporcionan descripciones cualitativas de orbitales de átomos con más de un solo electrón. Al introducir el concepto de cribado como una forma de representar las interacciones repulsivas entre los electrones de un átomo, se\(Z_{\rm eff}\) puede utilizar una carga nuclear efectiva en lugar de\(Z\) en el\(\psi_{n,l,m}\) y\(E_n\) para generar orbitales atómicos aproximados para ser llenados por electrones en muchos- átomo de electrones. Por ejemplo, en la aproximación más cruda de un átomo de carbono, los dos\(1s\) electrones experimentan la atracción nuclear completa así\(Z_{\rm eff} = 6\) para ellos, mientras que los\(2p\) electrones\(2s\) y son proyectados por los dos\(1s\) electrones, así\(Z_{\rm eff} = 4\) para ellos. Dentro de esta aproximación, uno ocupa entonces dos\(1s\) orbitales con\(Z = 6\), dos\(2s\) orbitales con\(Z = 4\) y dos\(2p\) orbitales con\(Z=4\) en la formación de la función de onda completa de seis electrones del estado de carbono de menor energía. Cabe señalar que el uso de cargas nucleares tamizadas como se acaba de discutir es diferente del uso de un parámetro de defecto cuántico d como se discutió en relación con los orbitales de Rydberg en el Capítulo 1. La carga\(Z = 4\) filtrada de carbono\(2s\) y\(2p\) orbitales está tratando de representar el efecto de los\(1s\) electrones de la capa interna en los\(2p\) orbitales\(2s\) y. La modificación del número cuántico principal realizada reemplazando\(n\) por\((n- d)\) representa la penetración de la órbita con el número cuántico nominal\(n\) dentro de sus conchas internas.

Colaboradores y Atribuciones

Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

Integrated by Tomoyuki Hayashi (UC Davis)