El principal uso de los logaritmos desde que John Napier los introdujo en el siglo XVII hasta nuestros tiempos, era como una herramienta que nos permitía realizar multiplicaciones con sumas. Esto gracias a la propiedad de los logaritmos que nos dice que y unas inmensas tablas de logaritmos. Esto permitió simplificar mucho los tediosos cálculos necesarios en ingeniería, astronomía y ciencias en general. Más allá de este uso inicial, que ahora ya es mucho menos relevante, los logaritmos tienen propiedades muy interesantes que siguen haciéndolos imprescindibles en todas estas disciplinas. Una de ellas es la de nos presenta la ley de Weber-Fechner que nos dice como nuestros sentidos reescalan la magnitud de un estímulo físico para permitir que su percepción sea la adecuada, de forma mucho más tolerante a los extremos. Por ejemplo, podemos ver perfectamente las estrellas en mitad del campo y nos costará mucho más en la ciudad donde la contaminación lumínica hará cambiar nuestra escala de percepción. O lo mismo pasará si contestamos una llamada telefónica en nuestra casa o en mitad de una discoteca, donde nos será más difícil por no decir imposible. ¿Qué pasaría si nuestros sentidos mantuvieran una escala lineal de percepción? Pues que o bien serían aptos para identificar estímulos en la parte baja de la escala, siendo los estímulos de la parte alta insoportables, o bien serían aptos para soportar los estímulos de la parte alta, siendo imperceptibles los de la parte baja. De forma empirica Fechner dedujo que la percepción  de un estimulo es proporcional al logaritmo de dicho estímulo entre el umbral a partir del cual dicho estímulo no es perceptible .

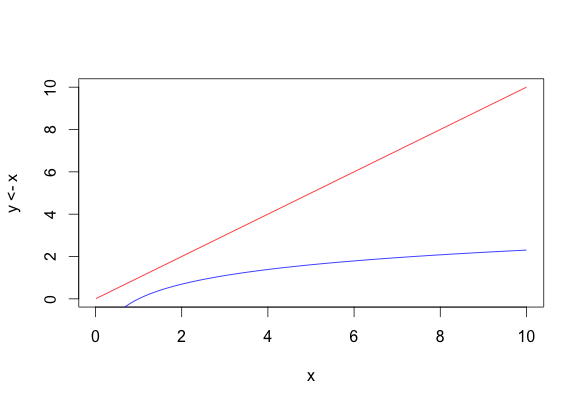
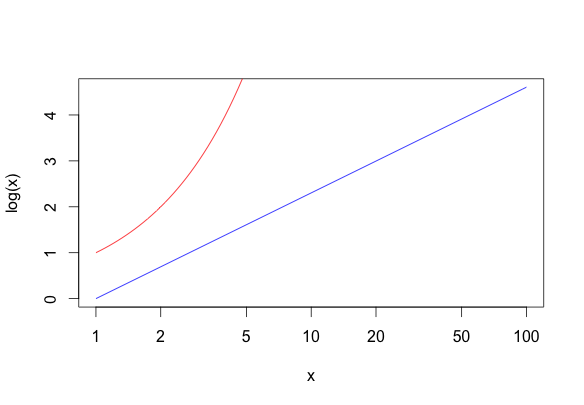
Siendo k una constante a calibrar empíricamente. Representando gráficamente la diferencia una función lineal y otra logarítmica utilizando ambas escalas podemos ver como el logaritmo de un estimulo con una escala logarítmica nos da la impresión de ser lineal, que es la percepción que tenemos de la realidad.

Escala lineal

Escala logarítmica

Y las funciones en R utilizadas para generar estas gráficas.

## Curvas y=x e y=log(x) con escala lineal
curve(y<-x, from = 0.01, to = 10, col = "red")
curve(log(x), from = 0.01, to = 10, add = TRUE, col = "blue")

## Curvas y=log(x) e y=x con escala logarítmica
curve(log(x), from = 1, to = 100, col = "blue", log="x")
curve(y<-x, from = 1, to = 100, add = TRUE, col = "red", log="x")

Derivando la ecuación anterior, podemos obtener como cambia la percepción respecto a un cambio en el estímulo.

¿Qué pasaría si extrapolásemos esta ley a la percepción del valor de un activo que tienen de los inversores ante su cambio en precio?. Esto ya se lo planteó MFM Osborne, siendo el primero en asociar el movimiento browniano al precio de las acciones, en un artículo de 1958, «Brownian motion in the stock market«.

En realidad esto es muy discutible, ya que supone que la percepción de un inversor sobre el valor real solo depende del precio del activo. Despreciando posibles eventos corporativos como los dividendos, publicación de resultados, cambios de gestión, etc.

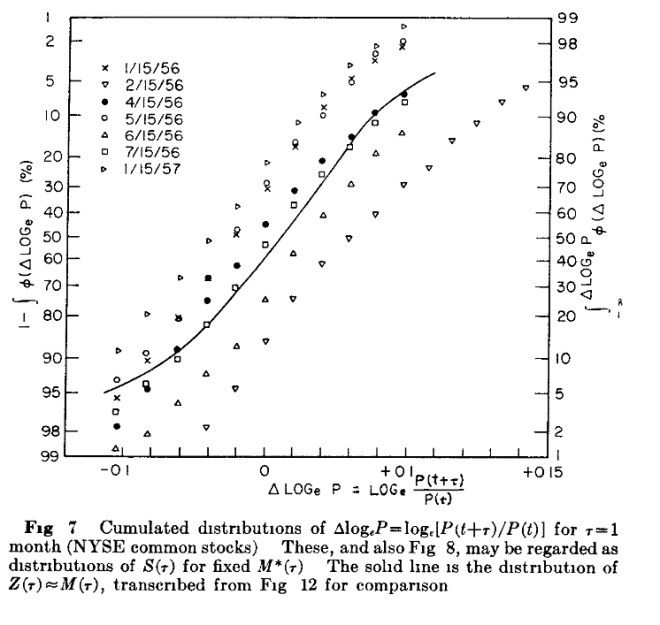
Pero Osborne infiere la ley de Weber-Fechner a partir de los datos de cotizaciones publicados en NYSE y ASE.

De hecho observa una distribución normal en los cambios de los logaritmos de los precios, es decir que los precios de los activos siguen una distribución lognormal. Lo que, como dice, sugiere que puede ser debido a que muchas variables aleatorias independientes contribuyen a estos cambios, como por otro lado parece lógico que ocurra.