6.2: 黑体辐射
- Page ID
- 201999
在本节结束时,您将能够:
- 应用维也纳定律和斯特凡定律分析黑体发出的辐射
- 解释普朗克的能量量假设
所有物体都会在一定波长范围内发射电磁辐射。 在前面的章节中,我们了解到凉爽的身体比温暖的身体散发的能量少。 通过观察,我们还知道,当人体被加热并且温度升高时,其发射辐射的感知波长会从红外变为红色,然后从红色变为橙色,依此类推。 随着温度的升高,人体会发出与越来越小的电磁频谱波长相对应的颜色发光。 这是白炽灯泡的基本原理:铁水灯丝会发出红光,当加热持续时,其发光最终会覆盖电磁光谱的整个可见部分。 发射辐射的物体或发射器的温度 (T) 决定了辐射能量达到最大值的波长。 例如,表面温度介于 5000 K 和 6000 K 之间的太阳,在电磁频谱的可见部分中,在大约 560 nm 的波长范围内辐射最强。 你的身体在大约300 K的正常温度下,在光谱的红外部分辐射最强。
入射到物体上的辐射会被部分吸收和部分反射。 在热力学平衡下,物体吸收辐射的速率与其发射辐射的速率相同。 因此,良好的辐射吸收器(任何吸收辐射的物体)也是很好的发射器。 完美的吸收体可以吸收所有入射在其上的电磁辐射;这样的物体被称为黑体。

尽管黑体是一种理想化,但由于没有物理物体能吸收 100% 的入射辐射,我们可以近距离实现黑体,其形式是在称为空腔散热器的密封外壳的墙壁上有一个小孔,如图所示\(\PageIndex{1}\)。 空腔散热器的内壁粗糙且变黑,因此任何通过空腔壁上的小孔进入的辐射都会被困在空腔内。 在热力学平衡时(温度为 T),空腔壁吸收的辐射量与发出的辐射量完全相同。 此外,在空腔内,进入孔的辐射与离开孔的辐射相平衡。 黑体的发射光谱可以通过分析从孔中辐射的光来获得。 黑体发出的电磁波称为黑体辐射。
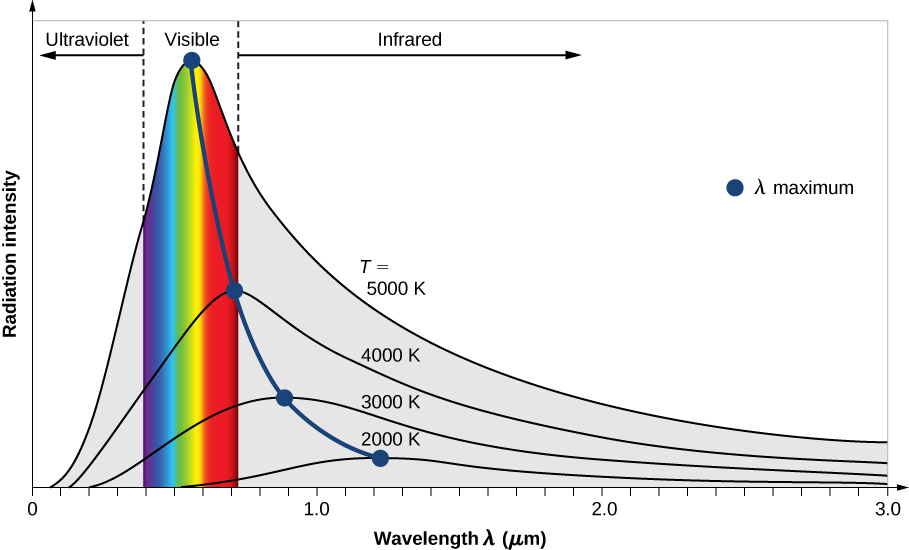
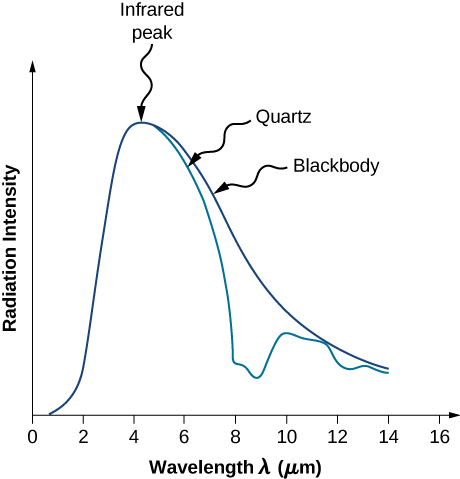
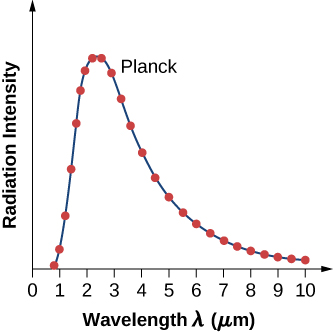
黑体辐射\(I(\lambda, T)\)的强度取决于发射辐射\(\lambda\)的波长和黑体的温度 T(图\(\PageIndex{2}\))。 函数\(I(\lambda, T)\)是每单位波长辐射的功率强度;换句话说,它是空腔辐射器中每单位波长的孔每单位面积辐射的功率。 根据这个定义,\(I(\lambda, T)d\lambda\)是在从\(\lambda\)到的波长间隔内发射的单位面积功率\(\lambda + d\lambda\)。 十九世纪末,通过实验研究了空腔发射的辐射波长之间的强度分布。 通常,材料发出的辐射仅大致遵循黑体辐射曲线(图\(\PageIndex{3}\));但是,普通恒星的光谱确实非常紧密地遵循黑体辐射曲线。
两个重要定律总结了黑体辐射的实验发现:维也纳位移定律和斯特凡定律。 图中连接强度曲线上最大值\(\PageIndex{2}\)的曲线说明了维也纳的位移定律。 在这些曲线中,我们可以看到人体越热,与辐射曲线中的发射峰相对应的波长越短。 从数量上讲,维也纳定律是
\[\lambda_{max}T = 2.898 \times 10^{-3} m \cdot K \label{Wien} \]
其中\(\lambda_{max}\)是辐射曲线中最大值的位置。 换句话说,\(\lambda_{max}\)是黑体在给定温度 T 下辐射最强的波长。 请注意,在方程\ ref {Wien} 中,温度以开尔文为单位。 维也纳的位移定律允许我们通过测量遥远恒星发出的辐射波长来估计它们的温度。
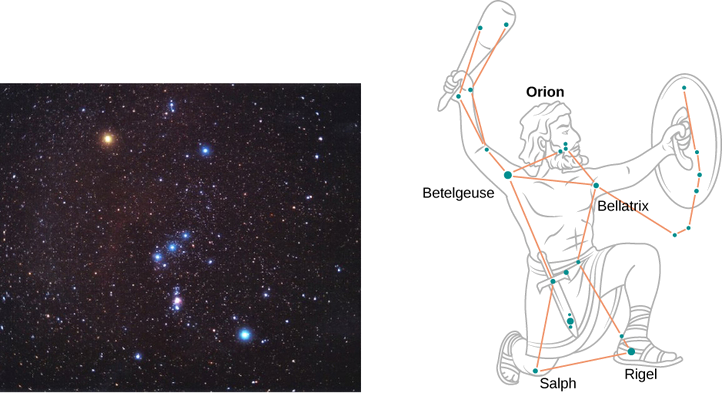
在冬季的一个晴朗的夜晚,如果你碰巧在北半球仰望天空,你可以看到猎户座(猎人)星座。 该星座中的一颗恒星 Rigel 以蓝色闪烁,另一颗恒星 Betelgeuse 呈红色,如图所示\(\PageIndex{4}\)。 这两颗星中哪一颗更酷,Betelgeuse 还是 Rigel?
策略
我们将每颗星星都当作黑体对待。 然后,根据维也纳定律,它的温度与其峰值强度的波长成反比。 蓝光\(\lambda_{max}^{(blue)}\)的波长比红光\(\lambda_{max}^{(red)}\)的波长短。 即使我们不知道精确的波长,我们仍然可以设定一个比例。
解决方案
为蓝星和红星写维也纳定律,我们有
\[\begin {align*} \lambda_{max}^{(red)}T_{(red)} &= 2.898 \times 10^{-3} m \cdot K \\[5pt] &= \lambda_{max}^{(blue)} T_{(blue)} \end{align*} \nonumber \]
简化后,这给出了
\[T_{(red)} = \dfrac{\lambda_{max}^{(blue)}}{\lambda_{max}^{(red)}}T_{(blue)} < T_{(blue)} \nonumber \]
因此,槟榔比锐佳凉爽。
意义
请注意,维也纳的位移定律告诉我们,发射体的温度越高,它发出的辐射的波长越短。 本示例中介绍的定性分析通常对任何发射体都有效,无论是诸如恒星之类的大物体还是诸如白炽灯泡中的发光灯丝之类的小物体。
第二个实验关系是斯特凡定律,它涉及在给定温度下在整个波长光谱上发射的黑体辐射的总功率。 在中\(\PageIndex{2}\),该总功率由给定 T 的黑体辐射曲线下的面积表示。 随着黑体温度的升高,总发射功率也会增加。 从定量上讲,斯特凡定律将这种关系表达为
\[P(T) = \sigma AT^4 \nonumber \]
其中\(A\)是黑体的表面积,\(T\)是其温度(以开尔文为单位),\(σ\)是 Stefan—Boltzmann 常数\(\sigma = 5.670 \times 10^{-8} W/(m^2 \cdot K^4)\)。 斯特凡定律使我们能够通过远程测量恒星的温度来估计恒星正在辐射多少能量。
像我们的太阳这样的恒星最终将演变为 “红巨星”,然后演变为 “白矮星”。 典型的白矮星大约相当于地球的大小,其表面温度约为\(2.5 \times 10^4 K\)。 典型的红巨人的表面温度为\(3.0 \times 10^3 K\),半径比白矮星大约 100,000 倍。 每单位面积的平均辐射功率和每种恒星辐射的总功率是多少? 它们如何比较?
策略
如果我们将恒星视为黑体,那么根据斯特凡定律,恒星辐射的总功率与其温度的第四次功率成正比。 要计算表面单位面积的辐射功率,我们无需对恒星的形状进行任何假设,因为 P/A 仅取决于温度。 但是,要计算总功率,我们需要假设能量通过围绕恒星的球形表面辐射,因此表面积为\(A = 4\pi R^2\),其中 R 是其半径。
解决方案
基于斯特凡定律的简单比例给出
\[\dfrac{P_{dwarf}/A_{dwarf}}{P_{giant}/A_{giant}} = \dfrac{\sigma T_{dwarf}^4}{\sigma T_{giant}^4} = \left(\dfrac{T_{dwarf}}{T_{giant}}\right)^4 = 4820 \label{6.5} \]
白矮星每单位面积发射的能量大约是红巨人发射功率的5000倍。 用方程式\ ref {6.5} 表示这个比率\(a=4.8×10^3\)
\[\dfrac{P_{dwarf}}{P_{giant}} = \alpha \dfrac{A_{dwarf}}{A_{giant}} = \alpha \dfrac{4\pi R_{dwarf}^2}{4\pi R_{giant}^2} = \alpha \left( \dfrac{R_{dwarf}}{R_{giant}} \right)^2 = 4.8 \times 10^{−7} \nonumber \]
我们看到,白矮星发出的总能量只是红巨人发射的总能量的一小部分。 尽管其温度相对较低,但红巨人辐射的总能量远远超过白矮星的总功率,因为红巨人的表面积要大得多。 为了估计每单位面积发射功率的绝对值,我们再次使用斯特凡定律。 对于白矮星,我们获得
\[\dfrac{P_{dwarf}}{A_{dwarf}} = \sigma T_{dwarf}^4 = 5.670 \times 10^{-8} \dfrac{W}{m^2 \cdot K^4} (2.5 \times 10^4 \, K)^4 = 2.2 \times 10^{10} \dfrac{W}{m^2} \label{6.7} \]
红巨人的类似结果是通过缩放白矮星的结果获得的:
\[\dfrac{P_{giant}}{A_{giant}} = \dfrac{2.2 \times 10^{10}}{4.82 \times 10^3} \dfrac{W}{m^2} = 4.56 \times 10^6 \dfrac{W}{m^2} \cong 4.6 \times 10^{-6} \dfrac{W}{m^2} \nonumber \]
意义
原则上,我们可以使用方程\ ref {6.7} 来估计白矮星发射的总功率。 但是,要找到它的表面积,我们需要知道平均半径,本例中没有给出平均半径。 因此,解决方案到此为止。 红巨星也是如此。
铁制扑克正在加热。 随着温度的升高,扑克开始发光——首先是暗红色,然后是亮红色,然后是橙色,然后是黄色。 使用黑体辐射曲线或维也纳定律来解释发光颜色的这些变化。
- 回答
-
辐射最大值的波长随着温度的升高而降低。
假设两颗恒星\(α\)和\(β\),辐射的总功率完全相同。 如果恒星的半径\(α\)是恒星的三倍\(β\),那么这些恒星的表面温度的比例是多少? 哪一个更热?
- 回答
-
\(T_{\alpha}/T_{\beta} = 1/\sqrt{3} \cong 0.58\),所以星星\(\beta\)更热。
“黑体” 一词是古斯塔夫·基尔霍夫在 1862 年创造的。 黑体辐射曲线是通过实验得知的,但直到 1900 年,它的形状才得不到物理解释。 温度为 T 的黑体的物理模型是封闭在空腔中的电磁波(图\(\PageIndex{1}\))以及与空腔壁处于热力学平衡状态的电磁波的物理模型。 波浪可以与墙壁交换能量。 这里的目标是找出不同波长(或频率)下各种振动模式之间的能量密度分布。 换句话说,我们想知道单个波长或波长波段携带了多少能量。 一旦我们知道了能量分布,我们就可以使用标准统计方法(类似于上一章中研究的方法)来获得黑体辐射曲线、斯特凡定律和维也纳位移定律。 当物理模型正确时,理论预测应与实验曲线相同。
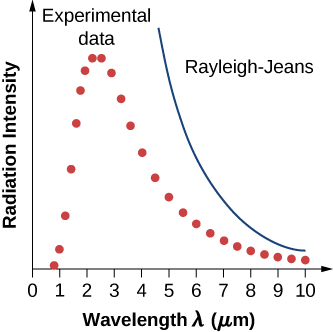
在解决黑体辐射问题的经典方法中,将辐射视为波浪(正如你在前几章中所研究的那样),捕获在空腔中的电磁波模式处于平衡状态,并不断与空腔壁交换能量。 波浪没有物理上的理由要不这样做:任何数量的能量都可以交换,要么通过从波浪转移到墙中的物质上,要么被波浪从墙中的物质中接收。 这幅经典照片是瑞利勋爵和詹姆斯·吉恩斯爵士独立开发的模型的基础。 这种经典的黑体辐射曲线模型的结果被称为 Rayleigh—Jeans 定律。 但是,如图所示\(\PageIndex{5}\),Rayleigh—Jeans 定律未能正确重现实验结果。 在短波长的极限下,Rayleigh—Jeans 定律预测了无限的辐射强度,这与实验结果不一致,在光谱的紫外线区域辐射强度具有有限值。 经典理论和实验结果之间的这种差异(后来被称为紫外线灾难)表明经典物理学如何无法解释黑体辐射的机制。
1900 年,马克斯· 普朗克解决了黑体辐射问题。 从某种意义上说,普朗克使用了与 Rayleigh—Jeans 模型相同的想法,即他以经典的方式处理空腔内墙壁之间的电磁波,并假设辐射与空腔壁保持平衡。 普朗克在他的模型中引入的创新思想是假设腔体辐射来自空腔壁内的原子振荡,而这些振荡只能具有离散的能量值。 因此,捕获在空腔壁内的辐射只能以离散的量与壁交换能量。 普朗克关于离散能量值的假设,他称之为量子,假设空腔壁内的振荡器具有量化能量。 这是一个全新的概念,它超越了十九世纪的经典物理学,因为正如你在上一章中所学到的那样,在经典画面中,振荡器的能量可以呈现任何连续的值。 普朗克假设振荡器 (\(E_n\)) 的能量只能有离散或量化的值:
\[E_n = nhf, \, where \, n = 1,2,3, \ldots \label{eq30} \]
在方程式\ ref {eq30} 中,\(f\)是普朗克振荡器的频率。 列举\(n\)这些离散能量的自然数称为量子数。 物理常数\(h\)称为普朗克常数:
\[h = 6.626 \times 10^{-34} J \cdot s = 4.136 \times 10^{-15} eV \cdot s \label{6.10} \]
每个离散能量值对应于普朗克振荡器的量子态。 量子态由量子数列举。 例如,当普朗克的振荡器处于其第一个\(n 1\)量子态时,其能量为\(E_1 = hf\);当它处于\(n = 2\)量子态时,其能量为\(E_2 = 2hf\);当它处于\(n = 3\)量子态时,\(E_3 = 3hf\)依此类推。
请注意,方程\ ref {eq30} 显示有无限多的量子态,可以表示为序列 {hf、2 hf、3 hf、...、(n — 1) hf、(n + 1) hf、...}。 该序列中每两个连续的量子态都由能量跳跃分开\(\delta E = hf\)。 壁中的振荡器可以从空腔中的辐射中接收能量(吸收),也可以向空腔中的辐射释放能量(发射)。 吸收过程将振荡器发送到更高的量子态,而发射过程将振荡器发送到较低的量子态。 无论这种能量交换走哪条路,可以交换的最小能量都是 hf。 可以交换多少能量没有上限,但是交换的任何能量都必须是 hf 的整数倍数。 如果能量包没有这个精确的量,它既不会被吸收,也不会在黑体墙上发射。
普朗克关于能量量子的假设指出,振荡器发射的能量由辐射量子携带,\(\Delta E\):
\[\Delta E = hf \label{planck} \]
回想一下,电磁辐射的频率与其波长和光速有关,基本关系\(f\lambda = c\). This means that we can express方程\ ref {6.10} 在波长方面是等效的\(\lambda\). When included in the computation of the energy density of a blackbody, Planck’s hypothesis gives the following theoretical expression for the power intensity of emitted radiation per unit wavelength:
\[I(\lambda, T) = \dfrac{2\pi hc^2}{\lambda^5} \dfrac{1}{e^{hc/\lambda k_BT} - 1} \label{6.11} \]
其中 c 是真空中的光速,kbKB 是玻尔兹曼常数,\(k_B = 1.380 \times 10^{-23} J/K\)。 方程\ ref {6.11} 中表示的理论公式称为普朗克的黑体辐射定律。 该定律与实验黑体辐射曲线一致(图\(\PageIndex{2}\))。 此外,维也纳的位移定律和斯特凡定律都可以从方程\ ref {6.11} 中推导出来。 为了得出维也纳的位移定律,我们使用微分微积分来找出辐射强度曲线的最大值\(I(\lambda, T)\)。 为了得出 Stefan 定律并找出 Stefan—Boltzmann 常数的值,我们使用积分微积分和积分来计算黑体在从\(\lambda = 0\)到的整个波长光谱中在一个温度下辐射的总功率\(\lambda = \infty\)。\(I(\lambda, T)\) 本章后面将把这个推导作为练习留下来。
图中空腔壁中的量子振荡器的振动频率\(\PageIndex{1}\)为\(5.0 \times 10^{14} Hz\)。 计算其能量水平之间的间隔。
策略
量子振荡器的能量态由方程\ ref {eq30} 给出。 能量间距\(\Delta E\)是通过找到量子数 n + 1 和 n 的两个相邻量子态之间的能量差来获得的。
解决方案
我们可以将给定的频率和普朗克常数直接代入方程中:
\[\begin {align*} \Delta E &= E_{n + 1} − En = (n + 1)hf − nhf \\[5pt] &= hf \\[5pt] &= (6.626 \times 10^{−34} \, J \cdot s)(5.0 \times 10^{14} \, Hz) \\[5pt] &= 3.3 \times 10^{− 19} \, J \end{align*} \nonumber \]
意义
请注意,我们没有指定使用哪种材料来建造空腔。 在这里,量子振荡器是墙壁中原子或材料分子的理论模型。
分子的振动频率为\(5.0 \times 10^{14}\, Hz\)。 它的振动能量水平之间的最小间距是多少?
- 回答
-
\(3.3 \times 10^{-19} J\)
一个 1.0 千克的质量在弹簧末端振荡,弹簧常数为 1000 N/m。这些振荡的振幅为 0.10 m。使用量化概念来找出这个经典振荡器的能量间距。 能量量化对于像这个振荡器这样的宏观系统有意义吗?
策略
我们使用方程\ ref {planck} 就好像系统是量子振荡器一样,但是质量的频率 f 在弹簧上振动。 为了评估量化是否具有显著影响,我们将量子能量间距与该经典振荡器的宏观总能量进行了比较。
解决方案
对于弹簧常数\(k = 1.0 \times 10^3 N/m\),\(m = 1.0 \, kg\)质量的频率 f 为
\[f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}} = \dfrac{1}{2\pi} \sqrt{\dfrac{1.0 \times 10^3 N/m}{1.0 \, kg}} \simeq 5.0 \, Hz \nonumber \]
对应于该频率的能量量子是
\[\Delta E = hf = (6.626 \times 10^{-34} J \cdot s)(5.0 \, Hz) = 3.3 \times 10^{-33} J \nonumber \]
当振动有振幅时\(A = 0.10 \, m\),振荡的能量为
\[E = \dfrac{1}{2} kA^2 = \dfrac{1}{2}(1000 \, N/m)(0.1 \, m)^2 = 5.0 \, J \nonumber \]
意义
因此,对于经典的振荡器,我们有\(\Delta E/E \approx 10^{-34}\)。 我们看到能量水平的分离非常小。 因此,出于所有实际目的,经典振荡器的能量采用连续值。 这就是为什么经典原理可以在不损失准确性的情况下应用于日常生活中遇到的宏观系统的原因。
如果质量不\(\PageIndex{4}\)是 1.0 kg 而是 1.0 µg 的微小质量,并且振动幅度为 0.10 µ m,示例中的结果会有所不同吗?
- 回答
-
不,因为那样\(\Delta E /E \approx 10^{-21}\)
当普朗克首次发表研究结果时,物理界并没有认真对待能量子的假设,因为它没有源于当时任何既定的物理理论。 即使普朗克本人也认为这是一种有用的数学技巧,可以很好地在理论上 “拟合” 实验曲线。 1905年,当爱因斯坦发表对光电效应的解释时,这种看法发生了变化,他在解释中赋予了普朗克的能量量子一个新的含义:光粒子的含义。


