La definición segunda del Libro Primero de los Elementos de Euclides dice que una línea (curva) es una longitud sin anchura. Esto significa que, según la geometría clásica, una curva no tiene anchura (ni los puntos extensión) y, por lo tanto, no tiene área y ni con una curva ni con varias sería posible llenar una superficie (por ejemplo, un cuadrado).
También se supone que la longitud de una curva es finita y es algo anómalo o, cuando menos sorprendente, que sea posible unir dos puntos A y B señalados en una hoja de papel con un camino de longitud infinita, que será mayor que el Diámetro del Universo observable que es de 93.000 millones de años luz.
Una curva plana la podemos imaginar como la trayectoria del paseo de una hormiga sobre el plano con un sentido de recorrido que haga corresponder a cada instante del tiempo de su paseo el punto (x, y) donde se encuentra la hormiga en ese momento. De forma general podemos definir curva plana C así:
Definición 1. Una curva C ⊂ R2 es un conjunto de puntos del plano que puede describirse mediante una aplicación α que asocia a cada parámetro t ϵ [a, b] un punto de R2 . α: [a, b] → R2 ]
Más precisamente, C es una curva de R2 si existen funciones x(t), y(t) definidas en un intervalo [a, b] tales que (x, y) ∈ C si y sólo si existe t ∈ [a, b] tal que x = x(t) e y = y(t) C ={(x(t), y(t)) ϵ R2, t ϵ [a, b]}
Para nuestros propósito distinguiremos los siguientes tipos de curvas:
Curva cerrada: Una curva en R2 es cerrada si α(a) = α(b) , es decir, si el origen y el extremo de la curva coinciden.
Curva simple: Una curva en R2 es simple si no tiene autointersecciones, esto es, si no se corta a si misma.
Curva de Jordan: Una curva en R2 se llama de Jordan si es cerrada y simple. Es decir, si puede deformarse de forma continua (sin romperse) hasta convertirse en una circunferencia. Por ejemplo, la curva siguiente:
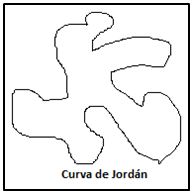
De la propia definición de cueva de Jodan se despende que toda curva plana de Jordan divide al plano en dos componentes conexas y disjuntas que tienen a la curva como frontera común. Una de estas componentes está acotada (la interior de la curva) y la otra componente no acotada y se le llama exterior.
Las curvas de Jordan , aunque cerradas y simples pueden presentar formas complicadas y mostrar un aspecto tan laberíntico y complejo que, en ocasiones, no es fácil distinguir a simple vista el interior y el exterior de la curva.
Por ejemplo, en la siguiente figura ¿Dónde está el punto A, en el interior o en el exterior de la curva? El teorema de Jordan proporciona un criterio para saber si el punto A está en el interior o en el exterior de una curva de Jordan.
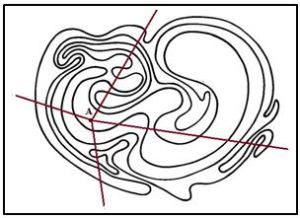
El criterio de Jordan es el siguiente, elegimos otro punto B que esté en el exterior de la curva. Y los unimos con el segmento A hasta B. Entonces, si el número de puntos de corte del segmento rectilíneo AB y con la curva es par, entonces el punto A está en el exterior de la curva y si el número de puntos de corte es impar, el punto A está en el interior de la curva. El matemático francés C. Jordan (1838-1922) publicó en su Cours d’Analyse una demostración de este resultado.
Podemos recordar nuestas ideas preconcebidas sobre las características que debe tener una buena curva. En nuestro subconsciente está la idea de que una curva es la trayectoria de un punto ideal en el plano, por lo tanto, la distancia entre dos de sus puntos no puede ser infinita, ya que el punto tardaría tiempo infinito en recorrerla y esa situación no se puede dar en la vida real. Además, una curva debe ser suave, sin muchos cambios bruscos de dirección y, por supuesto, que no cambie de dirección en cada punto, lo que significa, en el campo de las matemáticas que las curvas no deben ser picudas y que deben ser derivables en casi todos los puntos. Esas situaciones llevarían a curvas raras que en la literatura matemática comenzatron a llamarse curvas patológicas.
Podemos Imaginar una hormiga diminuta caminando de forma tan anómala que en cada punto del plano tira un dado y cambia la dirección según el resultado del lanzamiento ¿Qué sentido tiene en dinámica cambiar de dirección en cada punto?
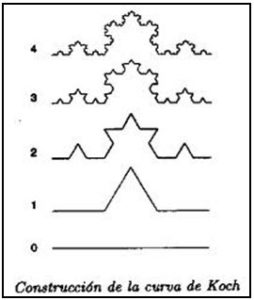
En 1904 el matemático sueco N.F.H. von Koch (1870-1924) describió la formación de la Curva Copo de Nieve, o curva de Koch, que no es derivable en ningún punto (cambia la dirección en cada punto) y, además, tiene longitud infinita Estas curva tiene una regla de formación iterativa. Su construcción es como sigue:
Nivel 0: Se toma un segmento de longitud a,
Nivel 1: Se divide el segmento en tres partes iguales y se remplaza la parte central por dos segmento igual longitud (a/3) formando un ángulo de 60º. Teniendo cuatro segmentos de longitud a/3.
Nivel 2: Con cada uno de los cuatro segmentos se prodece de igual forma lo que produce dieciséis segmentos de longitud a/9.
Se prosigle del mismo modo sucesiva e indefinidamente. La figura representa los cinco primeras pasos de la curva de Koch. En cada nivel la longitud de la curva se multiplica por 4/3, por tanto en el nivel n tendrá una longitud de a(4/3)n y su longitud será:
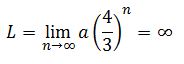
Pero las curvas patológicas siguen saltándose reglas. En el último cuarto del siglo XIX G. Cantor (1845-1918) estableció una biyección entre los puntos de un lado de cuadrado y el cuadrado, pero la biyección no era continua.
En 1891, G. Peano (1858-1932) en su artículo Sur une courbe qui remplit toute une aire plane, presentó una curva continua que llenaba el plano y construida de forma iterativa con los principios de la geometría elemental. Un año después D. Hilbert (1862-1943) hizo una variación sobre esta curva que se conoce como la Curva de Hilbert. Ambos matemáticos hallaron funciones continuas que aplicaban intervalo real [0,1] en cuadrado unidad. Eran correspondencias suprayectivas, pero no eran inyectivas (había puntos del cuadrado unidad con más de una imagen en el intervalo unidad).
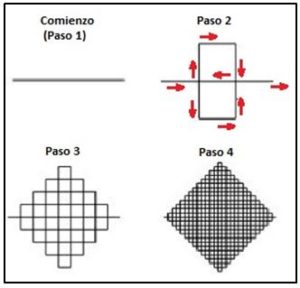
El algoritmo de construcción de la curva de Peano es similar al de la curva de Koch. Partiendo de un segmento rectilíneo cada segmento será remplazado por una línea quebrada.
Paso 1: Partimos de un segmento de longitud unidad.
Paso 2: Deducimos 9 nuevos segmentos, cada uno de longitud 1/3, que situamos en la disposición de la figura formada por nueve segmentos iguales.
Paso 3: Se aplica el paso 2 a cada uno de nueve segmentos …
El proceso indefinidamente.
Efectivamente esta curva llena el plano y parece contradecir el concepto de dimensión, geométrica, pero no es así porque la dimensión es un invariante topológico y las transformaciones que aquí aparecen no biyectivas y bicontinuas, no son homeomorfismos.