哈夫曼编码
一、哈夫曼编号:
又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。是一种高效的编码方式,在信息存储和传输过程中用于对信息进行压缩。
二、计算机系统如何存储信息
计算机不是人,它不认识中文和英文,更不认识图片和视频,它唯一“认识”的就是0(低电平)和1(高电平)。
因此,我们在计算机上看到的一切文字、图像、音频、视频,底层都是用二进制来存储和传输的。
从狭义上来讲,把人类能看懂的各种信息,转换成计算机能够识别的二进制形式,被称为编码。
编码的方式可以有很多种,我们大家最熟悉的编码方式就属ASCII码了。
在ASCII码当中,把每一个字符表示成特定的8位二进制数,比如:
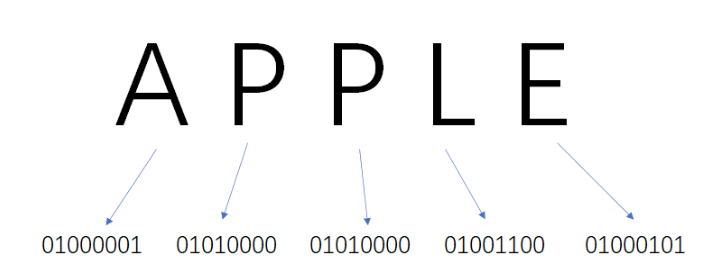
显然,ASCII码是一种等长编码,也就是任何字符的编码长度都相等。
等长编码
优点:因为每个字符对应的二进制编码长度相等,容易设计,也很方便读写。
缺点:计算机的存储空间以及网络传输的宽带是有限的,等长编码最大的缺点就是编码结果太长,会占用过多的资源。
为什么这么说呢?让我们来看一个例子:
假如一段信息当中,只有A,B,C,D,E,F这6个字符,如果使用等长编码,我们可以把每一个字符都设计成长度为3的二进制编码:
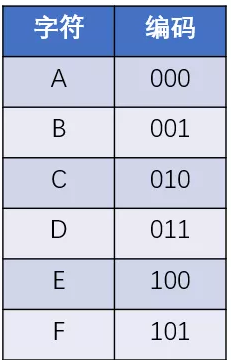
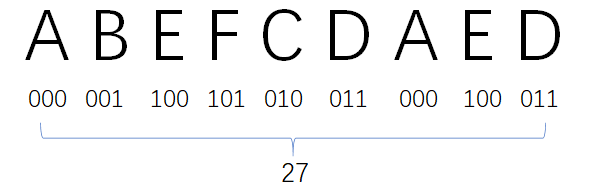
如此一来,给定一段信息 “ABEFCDAED”,就可以编码成二进制的 “000 001 100 101 010 011 000 100 011”,编码总长度是27。
但是,这样的编码方式是最优的设计吗?如果我们让不同的字符对应不同长度的编码,结果会怎样呢?比如:
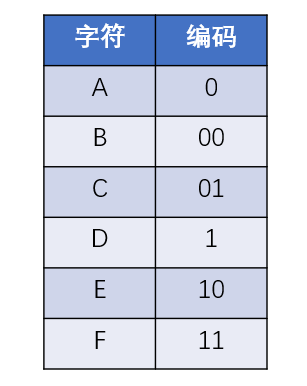
如此一来,给定的信息 “ABEFCDAED”,就可以编码成二进制的 “0 00 10 11 01 1 0 10 1”,编码的总长度只有14。
这样的编码设计可一使总长度大大缩短,但是这样设计会带来歧义,如A的编码是0,B的编码是00,那么000既可能代表AB也可能代表AAA,所有这种不定长的代码是不能随意设计的。
三、哈夫曼编码设计
哈夫曼编码(Huffman Coding),同样是由麻省理工学院的哈夫曼博所发明,这种编码方式实现了两个重要目标:
1.任何一个字符编码,都不是其他字符编码的前缀。
2.信息编码的总长度最小。
哈夫曼编码并不是 一套固定的编码,而是根据给的信息中各个字符出现的频次动态生成最优的编码。
这里引入一个哈夫曼树。
哈夫曼编码的生成过程是什么样子呢?让我们看看下面的例子:
假如一段信息里只有A,B,C,D,E,F这6个字符,他们出现的次数依次是2次,3次,7次,9次,18次,25次,如何设计对应的编码呢?
我们不妨把这6个字符当做6个叶子结点,把字符出现次数当做结点的权重,以此来生成一颗哈夫曼树:
第一步:构建森林

在上图当中,右侧是叶子结点的森林,左侧是一个辅助队列,按照权值从小到大存储了所有叶子结点。至于辅助队列的作用,我们后续将会看到。
第二步:选择当前权值最小的两个结点,生成新的父结点
借助辅助队列,我们可以找到权值最小的结点2和3,并根据这两个结点生成一个新的父结点,父节点的权值是这两个结点权值之和:
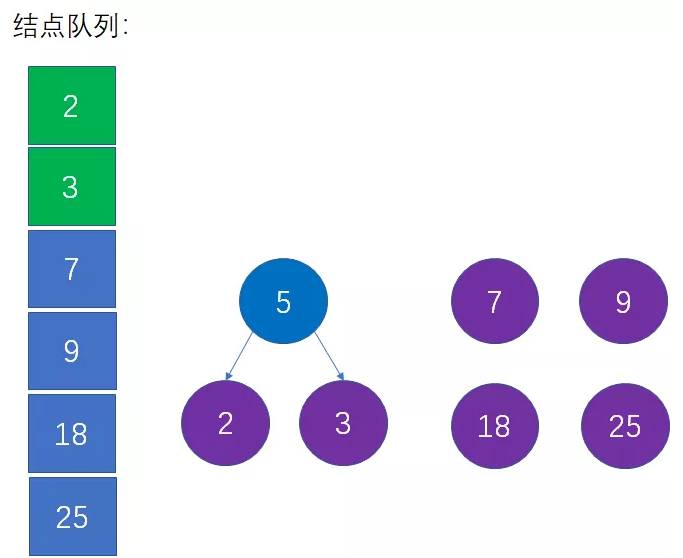
第三步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
也就是从队列中删除2和3,插入5,并且仍然保持队列的升序:
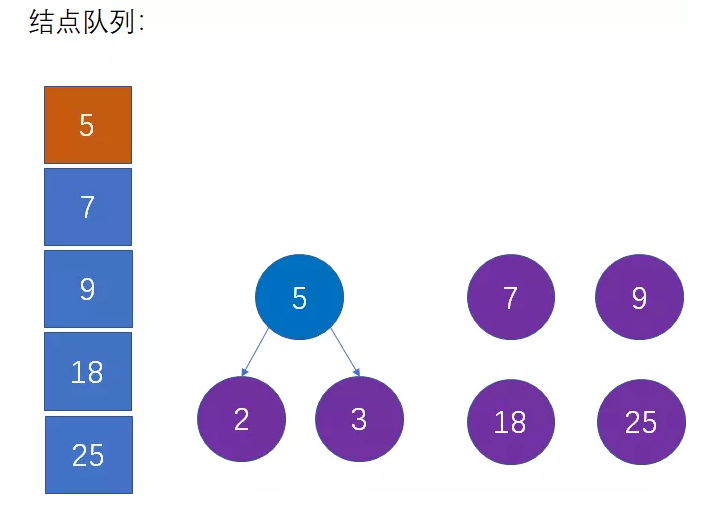
第四步:选择当前权值最小的两个结点,生成新的父结点
这是对第二步的重复操作。当前队列中权值最小的结点是5和7,生成新的父结点权值是5+7=12:
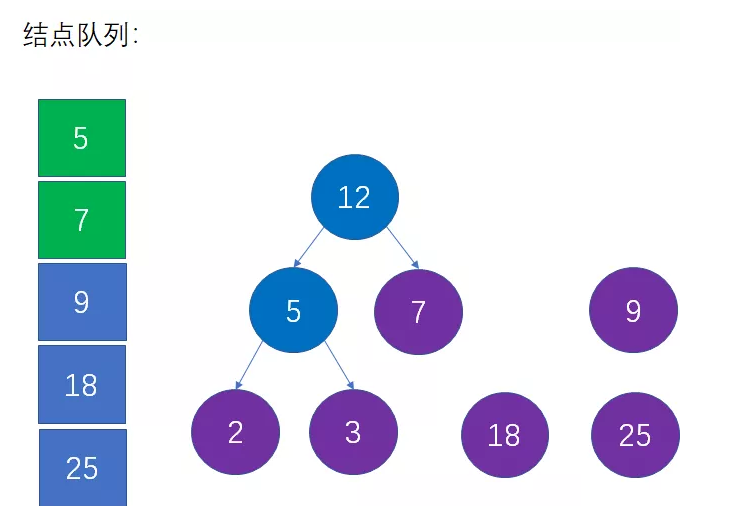
第五步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
这是对第三步的重复操作,也就是从队列中删除5和7,插入12,并且仍然保持队列的升序:
第六步:选择当前权值最小的两个结点,生成新的父结点
这是对第二步的重复操作。当前队列中权值最小的结点是9和12,生成新的父结点权值是9+12=21:
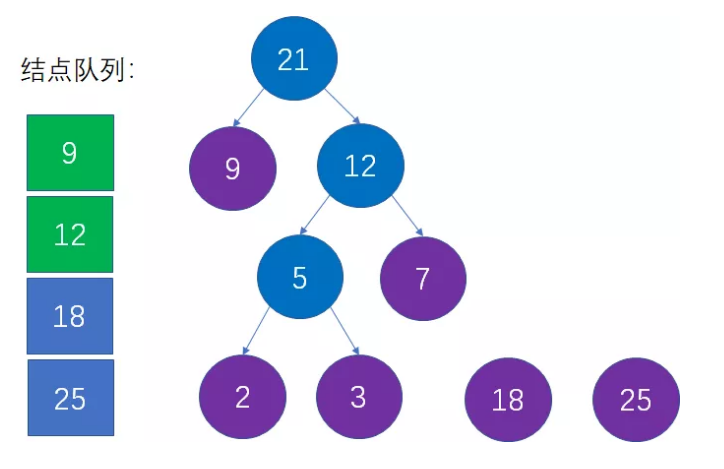
第七步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
这是对第三步的重复操作,也就是从队列中删除9和12,插入21,并且仍然保持队列的升序:
第八步:选择当前权值最小的两个结点,生成新的父结点
这是对第二步的重复操作。当前队列中权值最小的结点是18和21,生成新的父结点权值是18+21=39:
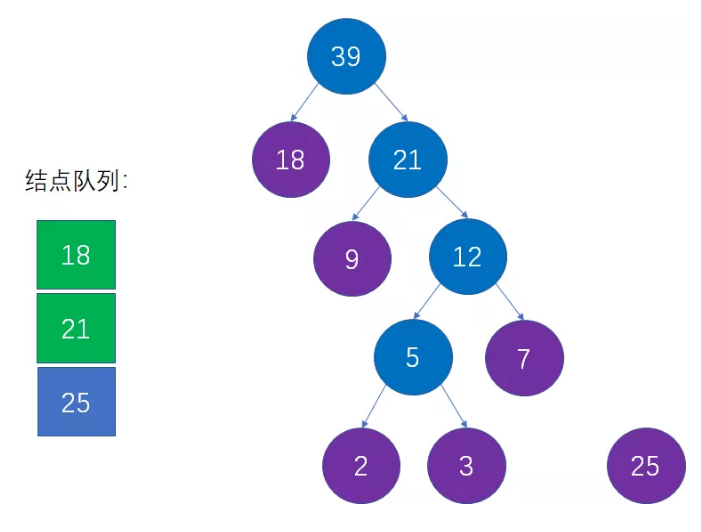
第九步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
这是对第三步的重复操作,也就是从队列中删除18和21,插入39,并且仍然保持队列的升序:
第十步:选择当前权值最小的两个结点,生成新的父结点
这是对第二步的重复操作。当前队列中权值最小的结点是25和39,生成新的父结点权值是25+39=64:
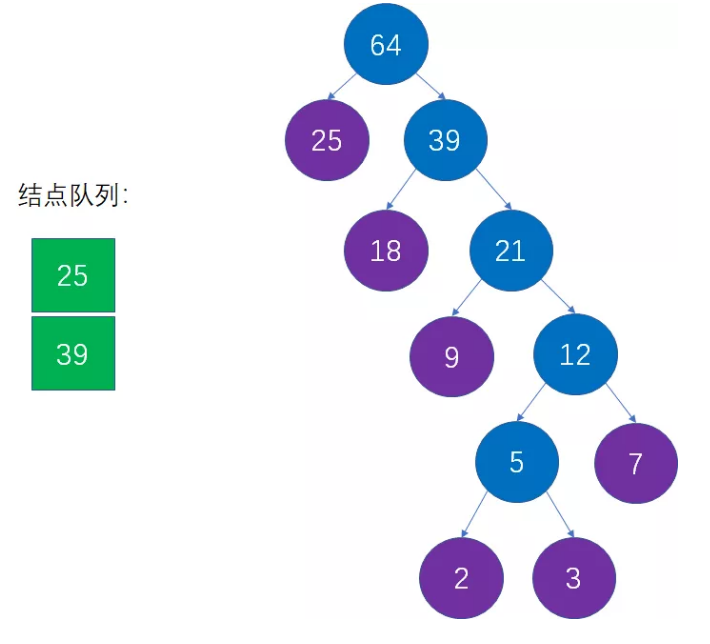
最终形成的哈夫曼数:
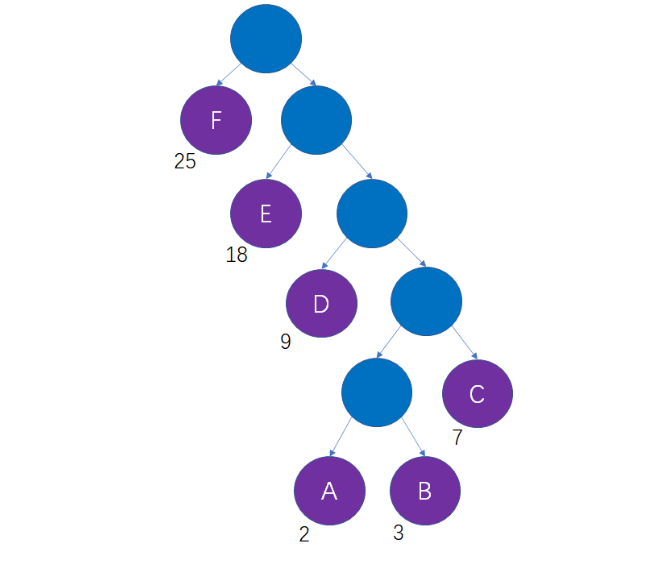
这样做的意义是什么呢?
哈夫曼树的每一个结点包括左、右两个分支,二进制的每一位有0、1两种状态,我们可以把这两者对应起来,结点的左分支当做0,结点的右分支当做1,会产生什么样的结果?

这样一来,从哈夫曼树的根结点到每一个叶子结点的路径,都可以等价为一段二进制编码:
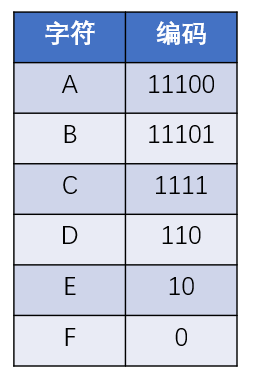
上述过程借助哈夫曼树所生成的二进制编码,就是哈夫曼编码。
现在,我们面临两个关键的问题:
首先,这样生成的编码有没有前缀问题带来的歧义呢?答案是没有歧义。
因为每一个字符对应的都是哈夫曼树的叶子结点,从根结点到这些叶子结点的路径并没有包含关系,最终得到的二进制编码自然也不会是彼此的前缀。
其次,这样生成的编码能保证总长度最小吗?答案是可以保证。
哈夫曼树的重要特性,就是所有叶子结点的(权重 X 路径长度)之和最小。
放在信息编码的场景下,叶子结点的权重对应字符出现的频次,结点的路径长度对应字符的编码长度。
所有字符的(频次 X 编码长度)之和最小,自然就说明总的编码长度最小

对比可以看出哈夫曼总长度要比定长编码短了超过20%
哈夫曼编码代码
private Node root; private Node[] nodes; //构建哈夫曼树 public void createHuffmanTree(int[] weights) { //优先队列,用于辅助构建哈夫曼树 Queue<Node> nodeQueue = new PriorityQueue<>(); nodes =new Node[weights.length]; //构建森林,初始化nodes数组 for(int i=0; i<weights.length; i++){ nodes[i]=new Node(weights[i]); nodeQueue.add(nodes[i]); } //主循环,当结点队列只剩一个结点时结束 while(nodeQueue.size()>1) { //从结点队列选择权值最小的两个结点 Node left = nodeQueue.poll(); Node right = nodeQueue.poll(); //创建新结点作为两结点的父节点 Node parent =new Node(left.weight +right.weight,left,right); nodeQueue.add(parent); } root =nodeQueue.poll(); } //输入字符下表,输出对应的哈夫曼编码 public String convertHuffmanCode(int index) { return nodes[index].code;} //用递归的方式,填充各个结点的二进制编码 public void encode(Node node, String code){ if(node ==null){ return; } node.code =code; encode(node.lChild, node.code+"0"); encode(node.rChild, node.code+"1");} public static class Node implements Comparable<Node>{ int weight; //结点对应的二进制编码 String code; Node lChild; Node rChild; public Node(int weight){ this.weight = weight; } public Node(int weight, Node lChild, Node rChild) { this.weight =weight; this.lChild = lChild; } @Override public int compareTo ( Node o ) { return new Integer ( this.weight ). compareTo ( new Integer ( o.weight )); } }
public static void main ( String [] args ) {
char [] chars = { 'A' , 'B' , 'C' , 'D' , 'E' , 'F' };
int [] weights = { 2 , 3 , 7 , 9 , 18 , 25 };
HuffmanCode huffmanCode = new HuffmanCode ();
huffmanCode.createHuffmanTree ( weights );
huffmanCode.encode ( huffmanCode.root , "" );
for (int i = 0; i < chars.length; i++) {
System.out.println(chars[i]+":"+ huffmanCode.convertHuffmanCode(i) );
}
}
}
这段代码中,Node类增加了一个新字段code,用于记录结点所对应的二进制编码。
当哈夫曼树构建之后,就可以通过递归的方式,从根结点向下,填充每一个结点的code值。




