数模 08排队论
排队论
排队系统的组成:
1.输入过程: 输入过程是说明顾客按照怎样的规律到达系统,分为三个方面:
顾客总数:有限与无限
顾客到达的方式:单个或者成批
顾客相继到达的时间间隔:确定型或者随机型
2.排队规则与服务规则:
排队规则:损失制、等待制、混合制
服务规则:先到先服务、后到先服务、随机服务、有优先权的服务
3.服务机构:
服务台数量及结构形式:数量上服务台有单台和多台之分,结构形式上服务台有单队-单服务台式、多队-多服务并列式、单队-多服务台并列式、单队-多服务台串列式、多服务混合式
服务方式:单个服务和成批服务
服务时间:确定型和随机型
排队模型的分类
记X:顾客到达的时间间隔分布;Y:服务时间的分布;Z:服务台数。
则排队模型为:X/Y/Z。
常用的记号:M—负指数分布;D—确定型;Ek—k阶Erlang分布;GI—一般相互独立的随机分布;G—一般随机分布。这里主要讨论M/M/1,/M/M/C。
到达间隔和服务时间典型分布

泊松流与指数分布
设x(t)为时间[0,t]内流事件发生的次数。例如[0,t]时间内到来的顾客数,[0,t]时间内服务台收到呼叫的此时。那么我们一般假定x(t)满足泊松过程,也称为poisson流或最简单流,表示[0,t]时间内事件发生次数为k次的概率服从泊松分布。
排队模型示例
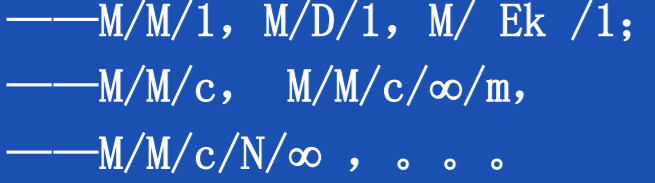
下面主要介绍mm1模型与mms模型。
首先,需要知道排队论模型的参数与一些常用概念公式








单服务台负指数分布M/M/1排队系统
条件为:
1、输入过程――顾客源是无限的,顾客到达 完全是随机的,单个到来,到达过程服从普阿 松分布,且是平稳的;
2、排队规则――单队,且队长没有限制,先 到先服务;
3、服务机构――单服务台,服务时间的长短 是随机的,服从相同的指数分布 。
公式为:

例题:



mms模型:
条件为:
此模型与M/M/1模型不同之处在于有S个服务台, 各服务台的工作相互独立,服务率相等,如果 顾客到达时,S个服务台都忙着,则排成一队 等待,先到先服务的单队模型。
整个系统的平均服务率为sμ,ρ*=λ/sμ, (ρ*<1)为该系统的服务强度。
公式为:


例题为:

下面,给出mms与mm1的matlab代码:

%***************************************** %初始化顾客源 %***************************************** %总仿真时间 Total_time = 10; %队列最大长度 N = 10000000000; %到达率与服务率 lambda = 10; mu = 6; %平均到达时间与平均服务时间 arr_mean = 1/lambda; ser_mean = 1/mu; arr_num = round(Total_time*lambda*2); events = []; %按负指数分布产生各顾客达到时间间隔 events(1,:) = exprnd(arr_mean,1,arr_num); %各顾客的到达时刻等于时间间隔的累积和 events(1,:) = cumsum(events(1,:)); %按负指数分布产生各顾客服务时间 events(2,:) = exprnd(ser_mean,1,arr_num); %计算仿真顾客个数,即到达时刻在仿真时间内的顾客数 len_sim = sum(events(1,:)<= Total_time); %***************************************** %计算第 1个顾客的信息 %***************************************** %第 1个顾客进入系统后直接接受服务,无需等待 events(3,1) = 0; %其离开时刻等于其到达时刻与服务时间之和 events(4,1) = events(1,1)+events(2,1); %其肯定被系统接纳,此时系统内共有 %1个顾客,故标志位置1 events(5,1) = 1; %其进入系统后,系统内已有成员序号为 1 member = [1]; for i = 2:arr_num %如果第 i个顾客的到达时间超过了仿真时间,则跳出循环 if events(1,i)>Total_time break; else number = sum(events(4,member) > events(1,i)); %如果系统已满,则系统拒绝第 i个顾客,其标志位置 0 if number >= N+1 events(5,i) = 0; %如果系统为空,则第 i个顾客直接接受服务 else if number == 0 %其等待时间为 0 2009.1516 %PROGRAMLANGUAGEPROGRAMLANGUAGE events(3,i) = 0; %其离开时刻等于到达时刻与服务时间之和 events(4,i) = events(1,i)+events(2,i); %其标志位置 1 events(5,i) = 1; member = [member,i]; %如果系统有顾客正在接受服务,且系统等待队列未满,则 第 i个顾客进入系统 else len_mem = length(member); %其等待时间等于队列中前一个顾客的离开时刻减去其到 达时刻 events(3,i)=events(4,member(len_mem))-events(1,i); %其离开时刻等于队列中前一个顾客的离开时刻加上其服 %务时间 events(4,i)=events(4,member(len_mem))+events(2,i); %标识位表示其进入系统后,系统内共有的顾客数 events(5,i) = number+1; member = [member,i]; end end end end %仿真结束时,进入系统的总顾客数 len_mem = length(member); %***************************************** %输出结果 %***************************************** %绘制在仿真时间内,进入系统的所有顾客的到达时刻和离 %开时刻曲线图(stairs:绘制二维阶梯图) stairs([0 events(1,member)],0:len_mem); hold on; stairs([0 events(4,member)],0:len_mem,'.-r'); legend('到达时间 ','离开时间 '); hold off; grid on; %绘制在仿真时间内,进入系统的所有顾客的停留时间和等 %待时间曲线图(plot:绘制二维线性图) figure; plot(1:len_mem,events(3,member),'r-*',1: len_mem,events(2,member)+events(3,member),'k-'); legend('等待时间 ','停留时间 '); grid on;

s=2; mu=4; lambda=3; ro=lambda/mu; ros=ro/s; sum1=0; for i=0:(s-1) sum1=sum1+ro.^i/factorial(i); end sum2=ro.^s/factorial(s)/(1-ros); p0=1/(sum1+sum2); p=ro.^s.*p0/factorial(s)/(1-ros); Lq=p.*ros/(1-ros); L=Lq+ro; W=L/lambda; Wq=Lq/lambda; fprintf('排队等待的平均人数为%5.2f人\n',Lq) fprintf('系统内的平均人数为%5.2f人\n',L) fprintf('平均逗留时间为%5.2f分钟\n',W*60) fprintf('平均等待时间为%5.2f分种\n',Wq*60)
对于mms,需要填入的参数为:
s
mu
lambda
输出为:

对于mm1,利用了仿真,输出:
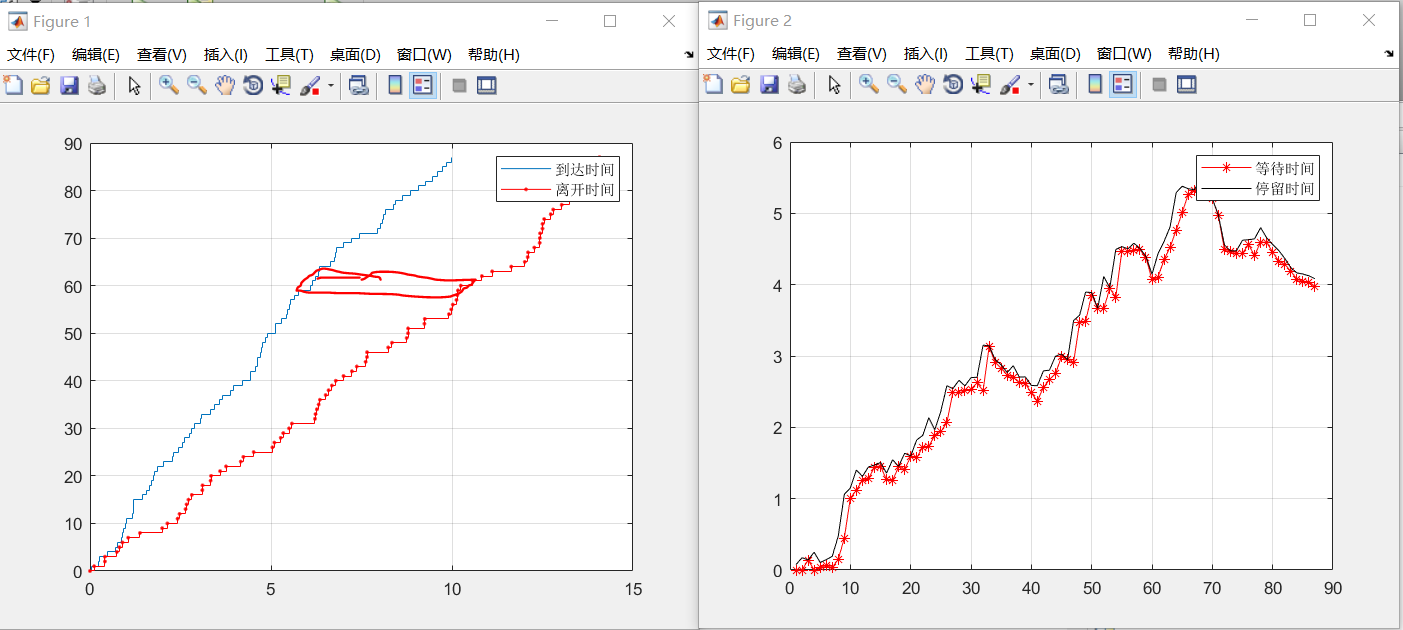
红笔描出的即为等待时间。
下面对一个具体实例进行演示:


可以看出是mms模型,由于我们需求的单位都是小时,所以换算
平均到达率为每分钟0.9人:54
平均服务率每分钟0.4人:24
修改参数为:
s=3;
mu=24;
lambda=54;
输出:




