1. 引言
在现实生活中,非人寿保险索赔的情况相对复杂,很难用共同分布对所有索赔金额数据进行建模,因为可能存在不止一个模型或未知分布,可以参见Agnes等人(2023) [1] 。在风险研究中,保险公司不关注整体数据,而只关注可能带来不可逆转风险的部分。在非人寿保险中,保单造成的巨额损失通常占索赔总额的很大比例如。如果发生重大损失,将带来严重后果。大损失的数量很少,这使得很难找到这部分数据的适当分布。非常有必要对保险索赔金额进行建模,特别是大额损失部分,这可以帮助保险公司做出决策,以计算保费,衡量尾部风险和找到最优再保险方案。保险索赔金额的分配在金融,保险和精算领域得到了广泛的研究,可以参见,Embrechts等人(1997) [2] ,Han and Jiang (1997) [3] ,McNeil (1997) [4] 等。
定义
是损失随机变量的概率空间。对于任何损失变量X,用
表示其分布函数,以及其中
其中
被认为是索赔严重性分布。
为了避免在某一特定风险承受水平下在规定的期限内破产,监管机构要求金融机构持有一定数量的风险准备金以满足其未来负债。保险公司通常使用风险度量来管理风险,例如风险价值,指在一定的置信水平下,金融资产(或投资组合)在未来特定时间段内的最大可能损失。对于VaR的研究,可以参见Xia等人(2023) [5] 、Peng等人(2023) [6] 。定义
,表示在水平
下,
我们可以发现,
;另外,其右端点为
。可以看出,索赔严重程度分布估计的准确性也会影响风险价值的估计。
Smith (1989) [7] 提出了一种利用极值理论(EVT)和广义Pareto分布(GPD)的理论构建复合模型的方法,称为超额阈值(EOT)或峰值阈值(POT)方法,可以参见Barlow等人(2023) [8] 。该方法广泛用于拟合非寿险数据的分布。该复合模型由两部分组成,分别对低于和高于阈值的索赔进行建模,可以参见Ghaddab等人(2023) [9] 。当然,这个阈值是通过一些方法预先确定的,包括图形诊断和启发式方法,可以在Davison和Smith (1990) [10] 、Gerstengarbe和Werner (1989) [11] 、Coles (2001) [12] 和DuMouchel (1983) [13] 、Ferreira等人(2003) [14] 、Loretan和Phillips (1994) [15] 、Stoev等人(2011) [16] 指出,这些图形诊断方法显然是主观的,并且可能对分布尾部的噪声或波动敏感。Wang等人(2020) [17] 认为,这些方法没有理论依据,但易于实施并在实践中频繁使用。Morever,Clauset等人(2009) [18] 提出超阈值分布对该阈值的选择非常敏感。因此,寻找合适的阈值选择方法尤为重要。此外,Scollnik (2007) [19] 推广了具有相应估计方法的复合模型,该方法允许同时估计阈值和其他模型参数。然而,在这种方法中,批量分布固定为对数正态分布。Wong和Li (2010) [20] 提出了一种复合模型,阈值仅在其中确定,参数通过最大间距乘积法(MPS)估算。不幸的是,他们考虑的复合模型是EOT模型。
在实践中,我们倾向于更关注上尾部的保险索赔。换言之,我们希望找到一种更简洁和基于统计的方法来选择阈值并估计保险索赔的上尾部的分布参数。Clauset等人(2009) [18] 提出了一个最大似然框架,该框架估计参数以及所选分布的下限,即分布的阈值。此外,Campolieti (2018) [21] 认为,最大似然框架允许模型选择和与替代分布的比较,以及评估拟合分布的拟合优度。这也是本篇文章使用最大似然框架方法的原因所在。该方法有助于我们在候选分布中找到最适合的分布来拟合保险索赔。我们希望使用一个通用且简单的分配模型来模拟我们关心的保险索赔。
本文的其余部分组织如下。第2节回顾了本文主要使用的三种候选分布模型和最大似然框架方法。第3节详细介绍了丹麦火灾保险数据集,并对数据集进行了描述性统计。第4节使用第2节中提到的方法对丹麦火灾保险数据进行建模和测试,并对结果进行分析和讨论。第5节给出了一些结论。
2. 模型和统计方法
回顾Kleiber和Kotz (2003) [22] 、Klugman等人(2012) [23] 、Andr和Bermudez (2020) [24] ,以及Bazyari (2023) [25] 文献,我们发现对保险索赔数据建模的研究通常集中于重尾分布。本文选取了大多数研究者广泛关注和研究的幂律分布、对数正态分布和威布尔分布。同时,这三种分布在许多重尾分布中也具有代表性。此外,在实践中,重要的是只考虑数据的上尾部,即超过阈值的数据部分。在一个世界中,我们考虑幂律分布、对数正态分布和在xmin处截断的威布尔分布,表示为
(2.1)
(2.2)
(2.3)
对于
,这里xmin是阈值,等价于使得模型成立的x值中最小值,以及
代表着正态分布的CDF。此外,
和
是各自模型的相应参数,需要通过统计方法进行估计。根据概率分布的规律性计算系数。不难发现,这三种分布模型都是右偏和重尾的。研究发现,每个分布的尾部衰减率都不同,其中正态分布大于对数正态分布和韦伯分布,这两种分布的尾部衰退率都大于幂律分布,但对数正态和韦伯分布的尾部衰变率相差不大。这意味着幂律分布的尾部更重,其次是对数正态分布和韦伯分布,最轻的是正态分布。
在本文中,我们使用最大似然(ML)估计模型参数。如Clauset等人(2009) [18] 所示,方程(2.1)中幂律分布指数α的最大似然估计量(MLE)可估计为
(2.4)
其中,
是x的观测值,并且
。显然,n是
的观测数,这也是上尾部的观测数。还可以计算其他两个模型参数
和
的MLE。为了简单起见,这里只给出幂律分布指数的MLE表达式。在方程(2.4)中,我们发现指数
的MLE是xmin的函数。换句话说,xmin的值对指数
的MLE有重要影响。Clauset等人(2009) [18] 证实,如果未正确选择xmin,幂律指数的MLE将与其真实值急剧偏离。这也是直觉上可以理解的。如果xmin小于实际xmin,则在估计时考虑不属于幂律分布的数据;如果xmin大于实际xmin,则在估计过程中将考虑较少的数据,这两者都会使估计不准确。不仅如此,我们还可以从方程(2.1)中判断。
Clauset等人(2007) [26] 提出了一种估计xmin的方法,该方法被认为更加客观和有原则。该方法选取xmin,以使观测数据与拟合的幂律分布之间的差异尽可能小,
(2.5)
其中
是值至少为xmin的观测数据的经验CDF,
为最适合
数据的幂律分布的CDF。因此,xmin的估计值,被表示为
,使方程(2.5)中的D最小化。
仅估计模型参数是不够的,还需要测试MLE方法的拟合优度,该方法生成一个p值,用于量化假设的合理性。本文使用了一种经典的测试方法,称为Kolmogorov-Smirnov测试(KS测试),适用于基础分布固定的情况。然而,在我们的例子中,由于xmin的不确定性,基础分布在不同的数据集之间有所不同。为了量化xmin估计中的不确定性,我们选择了Efron和Tibshirani (1993) [27] 详细介绍的非参数“bootstrap”方法。在计算KS测试的p值之后,我们需要使用p值来判断是拒绝幂律分布假设还是认为幂律假设分布是真的。如果
,则排除幂律分布假设。相反,人们认为幂律分布能够很好地拟合数据。我们认为,当用不同的分布拟合数据时,xmin的值是不同的,因此对其他两个分布进行了相同的KS检验。最后,我们根据KS测试的p值判断哪个分布更适合数据集。具有最高p值的分布被认为是候选分布中适合数据集的最佳分布。
3. 数据集和描述性统计
该数据集可以在R语言的SMPracticals包中找到。它由四个部分组成:建筑损失、内容物损失、利润损失、总损失,其中这四组的数据量分别为1990、1679、616、2167,对以丹麦克朗为单位的火灾损失索赔的观察结果,以1985年的价格来计算的。自Embrechts等人(1997) [2] 和McNeil (1997) [4] 首次考虑最后一组数据以来,许多学者对其进行了广泛研究,主要是关于哪种分布更适合这组数据。我们让读者参考Wong和Li (2010) [20] 、Lee等人(2012) [28] 、Nadarajah和Bakar (2014) [29] 、Wang等人(2020) [17] ,仅列举文献中的几个。
为了更直观地探索数据趋势,图1给出了丹麦火灾保险索赔的密度图。核密度估计是一种估计随机变量概率密度函数的非参数方法。核密度图本质上是一条直方图拟合曲线,可以看作是一个概率密度图。从图1中,我们可以清楚地观察到这四组数据中有很多右尾数据,并且有一些较大的值。这显然是一个右偏分布。但很难看出它是否是重尾分布。我们可以通过描述性统计进一步分析数据。此外,从图1中,我们还可以看到这些损失是非负的。
此外,表1给出了丹麦火灾数据集中四组数据的一些描述性统计数据。根据这组数据的平均值、中值、标准差、最大值和最小值,我们发现数据中存在较大的值,并且频率较低。这组数据的偏度和峰度表明它服从偏斜和重尾分布。偏度为0,两侧的尾部长度是对称的,例如,正态分布是对称分布。如果偏度小于0,则分布具有负偏差。它也被称为左偏。左尾巴比右尾巴长。如果偏度大于0,则分布具有正偏差。它也被称为右偏。右尾巴比左尾巴长。偏差的绝对值越大,分布的偏差越严重。峰度可以描述分布模式的陡度。如果峰度小于3,则称分布峰度不足,且分布平缓。如果峰度大于3,则该分布称为峰度过大,且分布陡峭。峰度的绝对值越大,其分布形式与正态分布之间的差异就越大。

Table 1. Descriptive statistics for Danish fire insurance claims, millions (of Danish Kroner)
表1. 丹麦火灾保险索赔的描述性统计,百万(丹麦克朗)
为了用右偏和厚尾分布建模和分析数据,我们需要选择一个具有相同两个财产的分布模型。如第2节所述,三个分布模型是右偏和重尾的。它们可以用于丹麦火灾保险数据的建模,这是合理的。
4. 实证结果和讨论
在第2节和第3节中,我们分别详细描述了丹麦火灾保险索赔数据集和三个候选分布模型的特征,并发现它们都具有右偏和重尾的特征。因此,将这三种候选分布作为丹麦火灾保险索赔数据的拟合分布是合理的。然而,仍然需要通过统计方法获得特定的参数值。表2给出了使用最大似然框架估计和测试每组数据分布的结果。从表2中,我们发现,对于建筑损失数据,幂律分布和对数正态分布的p值均是大于0.05的,并且对数正态分布的p值是大于幂律分布的的p,这表明对数正态分布比幂律分布更适合;对于内容物损失,幂律分布、对数正态分布以及韦布尔分布的p值均是大于0.05的,并且对数正态分布的p值是大于韦布尔分布的p值,这表明三种分布中对数正态分布最多;对于利润损失数据,幂律分布的p值是大于0.05的,对数正态分布以及韦布尔分布的p值均是小于0.05的,这意味着幂律分布可以描述这组数据;对于总损失组数据,幂律分布和对数正态分布的p值均是远远大于0.05,并且幂律分布的p值是大于对数正态分布的的p值的,这表示幂律分布可以描述这组数据。使用动态阈值选择方法,每组数据的尾部长度(即ntail相对合理。Clauset等人(2009) [18] 提到,当ntail较小时,应谨慎对待高p值。

Table 2. Estimates of power law, lognormal and weibull distributions for Danish fire data of four groups
表2. 对四组丹麦火灾数据进行幂律、对数正态和韦布尔分布估计
1它表示每个分布的参数估计。2它表示≥xmin的观察次数;括号中的数字表示数据总量。3这是2500次复制KS检验得出的p值。
我们根据图2~5中双对数尺度的数据绘制了三个候选分布(即,基于表2中的估计)。这些图片为四组丹麦火灾数据与我们估计的三个候选分布的拟合提供了视觉证据。从图2中,我们可以发现,建筑组数据的上尾部的大部分观测值都在图中虚线附近,只有少数观测值远离这条线。图2(1)和(2)都显示了这一特性,这也表明幂律分布和对数正态分布与建筑损失组数据非常吻合。对于图3,与(2)和(3)中的虚线相比,(1)中偏离虚线的观察值更多,这意味着对数正态分布和韦伯分布对内容物损失组数据的拟合优于幂律分布。对于图4,很明显,有许多观察结果偏离了(2)中的虚线。和(3)中存在明显的偏差点。相比之下,(1)中的观察结果更好地分布在虚线周围。这意味着幂律分布更符合利润损失组的数据。对于图5,只有(2)中的一些观察结果偏离虚线,(1)中的情况类似。这也意味着幂律分布和对数正态分布都能很好地拟合总损失组的数据。

Figure 2. Plot of the data for the Building group and fitted Power law and Lognormal distribution. Notes: vertical dashed line denotes estimate of xmin
图2. 对建筑损失组数据图拟合幂律分布、对数正态分布。注:垂直虚线表示xmin的估计值
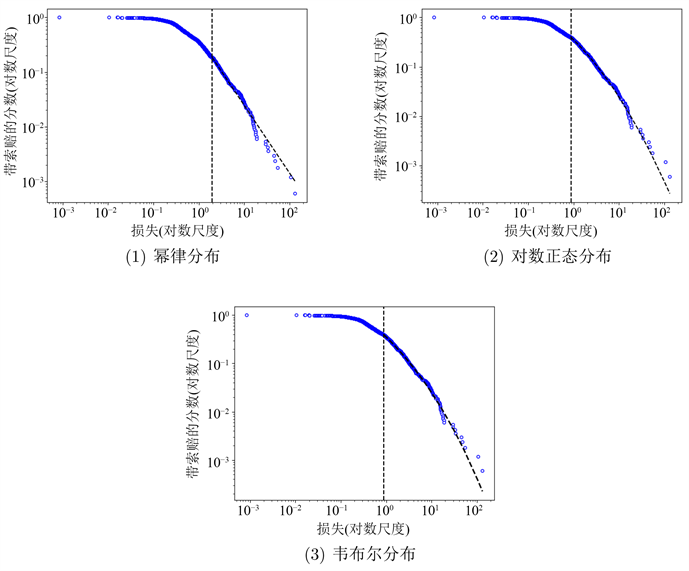
Figure 3. Plot of the data for the Contents group and fitted Power law, Lognormal and Weibull distribution. Notes: vertical dashed line denotes estimate of xmin
图3. 对内容物损失组数据图拟合幂律分布、对数正态分布和韦布尔分布。注:垂直虚线表示xmin的估计值
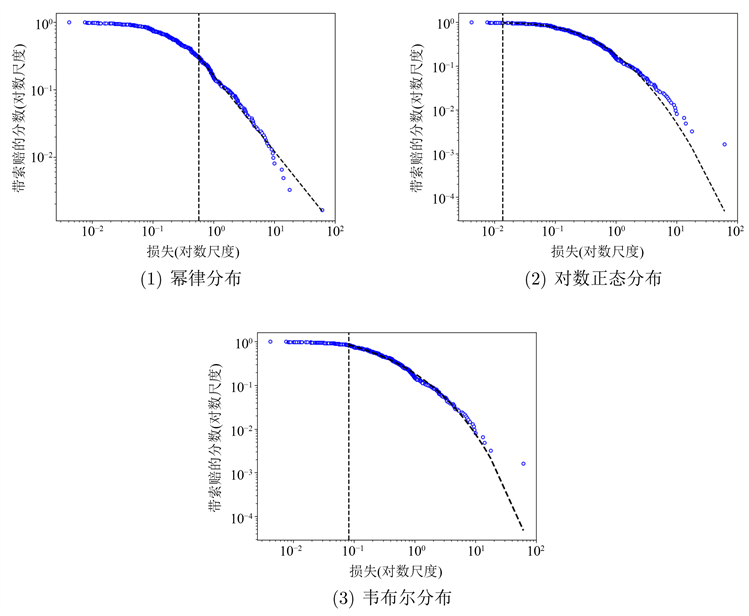
Figure 4. Plot of the data for the Profits group and fitted Power law, Lognormal and Weibull distribution. Notes: vertical dashed line denotes estimate of xmin
图4. 对利润损失组数据图拟合幂律分布、对数正态分布和韦布尔分布。注:垂直虚线表示xmin的估计值
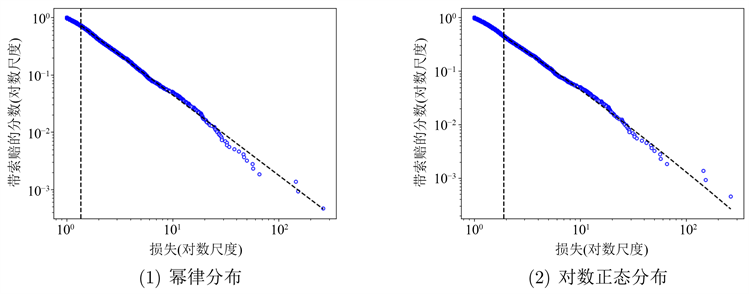
Figure 5. Plot of the data for the Total group and fitted Power law and Lognormal distribution. Notes: vertical dashed line denotes estimate of xmin
图5. 对总损失组数据图拟合幂律分布、对数正态分布和韦布尔分布。注:垂直虚线表示xmin的估计值
如上所述,阈值的选择对分布的估计和测试有一定的影响。我们想验证保险索赔数据是否也会产生这样的结果。因此,我们将数据中的最小值作为阈值,即对整个数据进行建模,结果如表3所示。我们可以发现,如果没有选择阈值来建模数据,测试的p值小于0.05,这拒绝了原始假设,也就是说,建立的模型不能很好地拟合丹麦火灾数据。表2中每组数据的每个分布的参数与表3中的值不同。这也证明,对于保险索赔数据,在建模之前选择阈值是有效的。

Table 3. Estimates of power law, lognormal and weibull distributions for Danish fire data of four groups, xmin equals minimum claim amount in each group
表3. 对四组丹麦火灾数据进行幂律、对数正态和韦布尔分布估计,xmin等于每组的最低损失金额
1它表示每个分布的参数估计。2它表示≥xmin的观察次数;括号中的数字表示数据总量。3这是2500次复制KS检验得出的p值。
表2中选择阈值的方法是动态的,这使我们想知道如果预先固定阈值,分布的估计和测试将如何受到影响。有几种方法可以预先确定阈值,包括固定分位数规则、平方根规则、经验规则、AMSE希尔估计量的最小值、指数检验、Gertensgarbe图。有关这些方法的详细信息,请参考Wang等人(2020) [17] 。使用上述六种方法的阈值选择结果如表4所示。我们可以发现,不同方法选择的阈值是非常不同的。

Table 4. Thresholds of each group of data under different threshold selection methods. Note: Numbers in parentheses indicate the number of observations ≥ xmin
表4. 不同阈值选择方法下每组数据的阈值。注意:括号中的数字表示≥xmin的观察次数
我们选择了一组尾部数据较多的数据进行验证,以确保分布估计和测试的可靠性的稳定性。通过比较分析,我们选择了根据AMSE 希尔估计量的最小值方法获得的每组丹麦火灾数据的阈值,结果见表5。

Table 5. Estimates of power law, lognormal and weibull distributions for danish fire data of four groups, xmin is determined by this method Minimum AMSE of the Hill estimator in each group
表5. 对四组丹麦火灾数据进行幂律、对数正态和韦布尔分布估计,各组的xmin通过AMSE希尔估计量的最小值方法所确定
1它表示每个分布的参数估计。2它表示≥xmin的观察次数;括号中的数字表示数据总量。3这是2500次复制KS检验得出的p值。
从表5可以看出,对于通过该方法选择的阈值,对于四组数据,建立的分布不是很稳定。对于具有大尾部数据的建筑损失组和总损失组数据,结果与动态阈值选择的结果相差不大。但是,对于尾部较小的内容物损失组和利润损失组数据,结果与动态阈值选择的结果有很大不同。内容物损失组数据中对数正态分布和韦布尔分布的测试结果(即p值)相对较低,这与表2中的值大相径庭。对于利润损失组数据,对数正态分布和韦布尔分布的p值与表中的p值相比非常大。我们可以观察到,利润损失组数据中ntail的值仅为71,这使得大p值的可信度较低。通常,动态选择阈值的方法更稳定。
如第1节所述,保险公司通常更关注偿付能力,例如风险价值。因此,我们还希望看到通过该方法估计的分布模型的性能,以预测VaR,结果如表6所示。对于建筑损失组数据,幂律分布预测的VaR值高于对数正态分布。显然,对数正态分布预测的VaR值更接近于经验分布。对于内容物损失组数据,对数正态分布和韦伯分布对VaR的预测相似,优于幂律分布。对于利润损失组数据,对数正态分布的预测VaR值低于经验VaR值。韦布尔分布预测的VaR值与经验VaR值非常接近,但仍有一个较低的值。幂律分布预测的VaR值更安全。对于总损失组数据,幂律分布对VaR有更好的预测,并且更接近经验VaR值。


Table 6. Comparison of predicted VaR and empirical VaR
表6. 比较预测的VaR和经验的VaR
丹麦火灾数据是一组经典数据。关于总损失组的数据已有很多文献,这是丹麦火险数据中数据最多的一组火灾保险数据集。这组数据已被许多学者广泛研究,其结果与本文的研究结果一致,见Scollnik (2007) [19] 、Wong和Li (2010) [20] 。数据集中剩余三组数据的建模结果也与经验判断一致。因此,在之后的研究中可以对重尾分布族的其他分布进行估计和检验,这样有助于研究保险索赔数据的重要性质以帮助解决实际问题。除此之外,还可以为保险索赔理论提供实证方面的研究。本文目前所研究的是单个保险索赔随机变量所服从的分布,未来希望研究如何能够估计和检验出多个具有某种相依结构的保险索赔随机变量的联合分布。
5. 结束语
在本文中,使用最大似然估计器来估计候选分布的参数和下限(即阈值)。此外,当对四组丹麦火灾数据进行建模时,该方法可以通过比较p值在三个候选分布中选择最佳拟合分布。这些结果与其他研究人员的结果一致,也与第4节中提到的经验判断相结合。众所周知,重尾分布中不仅有这三种分布,未来还可以估计和检验其他分布。本文可以作为保险索赔数据建模的启发式探索。此外,本文所述方法也可以为保险索赔的理论研究提供实证支持。我们关注的是,基于保险索赔数据建立的模型是否能够通过这样一种动态选择的阈值方法准确预测其风险度量指标。
基金项目
本文受2022年江苏省研究生科研创新计划项目资助(项目批准号:KYCX22_2212),项目名称:金融扭曲风险测度的渐近行为研究,类别:自然科学。
参考文献