La integral definida
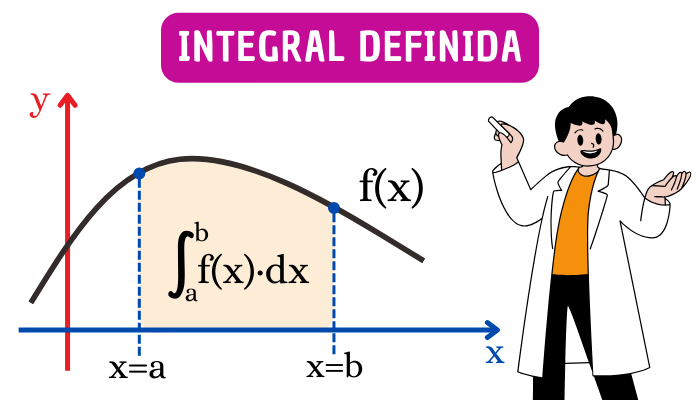
La integral definida es un concepto en cálculo integral que representa la acumulación de cantidades a lo largo de un intervalo específico. Se denota por: \[\int_{a}^{b}f(x)dx\] donde \(f(x)\) es la función que estamos integrando, y \(a\) y \(b\) son los límites inferior y superior del intervalo de integración.
La interpretación más común de la integral definida es que calcula el área bajo la curva de la función \(f(x)\) en el intervalo \([a, b]\). Si \(f(x)\) es no negativa en ese intervalo, la integral definida representa el área encerrada entre la curva y el eje \(x\), limitado por las líneas \(x=a\) y \(x=b\).
Además, si \(f(x)\) describe la tasa de cambio de alguna cantidad, la integral definida proporciona la acumulación total de esa cantidad en el intervalo \([a, b]\). Esto es útil para entender cómo se acumulan cantidades a lo largo del tiempo o de alguna variable independiente.
Propiedades de la integral definida
A continuación, te presentamos de manera detallada y con ejemplos las propiedades de la integral definida. Estas propiedades te ayudarán a comprender mejor el concepto de integral definida, además aprenderás cómo aplicarlas para resolver integrales definidas.
Integral definida de una función constante
Si \(f(x)\) es una función constante, es decir, \(f(x)=k\) para todo \(x\) en el dominio de \(f\), y además \(f\) es integrable en \(\left[a, b\right]\), entonces:
Esta propiedad establece que la integral definida de una función constante es igual al valor constante multiplicado por la longitud del intervalo \([a, b]\).
Es importante destacar que la integral definida proporciona el área bajo la curva de la función constante en el intervalo dado.
Integral definida de una función constante ejemplos
Ejemplo 1. Supongamos que tenemos la función constante \(f\) definida como \(f(x)=3\) en el intervalo cerrado \([2, 5]\). Queremos calcular la integral definida de \(f(x)\) en este intervalo, es decir, queremos hallar el valor de la siguiente integral definida: \[\int_{2}^{5}3dx\]
La propiedad de la integral definida para una función constante nos indica que podemos calcularla multiplicando la constante por la longitud del intervalo, es decir: \[\begin{aligned}\int_{2}^{5}f(x)dx&=\int_{2}^{5}3dx\\&=3(5-2)\\&=3(3)\\&=9\end{aligned}\]
Por lo tanto, la integral definida de la función constante \( f(x)=3\) en el intervalo \([2, 5]\) es igual a 9. Esto significa que el área bajo la curva de la función constante en ese intervalo es 9 unidades cuadradas.
En resumen, la integral definida de una función constante es simplemente el producto de la constante por la longitud del intervalo en el cual se está calculando la integral.
Integral definida del producto de una constante por una función
Si \(f\) es una función integrable en \([a, b]\) y \(k\) es una constante, entonces \(kf\) es integrable en \([a, b]\) y , además:
Esta propiedad establece que la integral definida del producto de una constante y una función es igual a la constante multiplicada por la integral definida de la función.
Integral definida del producto de una constante por una función ejemplos
Ejemplo 2. Supongamos que queremos calcular la integral definida de la función \(g\) definida como \(g(x)=4x^2\) en el intervalo \([0, 3]\).
De acuerdo con la propiedad de la integral definida del producto de una constante por una función, podemos sacar una constante fuera del símbolo de la integral definida. En este caso el valor de la constante \(k\) es \(k=4\), de tal manera que: \[\int_{0}^{3}4x^2dx=4\int_{0}^{3}x^2dx\] Resolviendo por separado la integral definida, obtenemos: \[\begin{aligned}\int_{0}^{3}x^2dx&=\left(\frac{x^3}{3}\right)\Big|_{0}^{3}\\&=\frac{3^3}{3}-\frac{0^3}{3}\\&=9-0\\&=9\end{aligned}\] De tal manera que: \[\begin{aligned}\int_{0}^{3}4x^2dx&=4\int_{0}^{3}x^2dx\\&=4(9)\\&=36\end{aligned}\] Por lo tanto, la integral definida de la función \( g(x) = 4x^2 \) en el intervalo \([0, 3]\) es igual a \(36\).
Integral definida de una suma de funciones
Si \(f\) y \(g\) son funciones integrables en el intervalo \([a, b]\), entonces \(f+g\) es integrable en \([a, b]\) y, además:
Esta propiedad establece que la integral definida de una suma de funciones es igual a la suma de las integrales definidas de cada función.
Integral definida de una suma de funciones ejemplos
Ejemplo 3. Supongamos que queremos calcular la integral definida de la función \(h\) definida como \(h(x)=2x+3\) en el intervalo \([1, 4]\). Para simplificar el cálculo, descompondremos la función en la suma de dos funciones más simples, es decir, sean \(f(x)=2x\) y \(g(x)=3\) tal que: \[\begin{aligned}h(x)&=f(x)+g(x)\\&=2x+3\end{aligned}\]
La propiedad de la integral definida de una suma de funciones nos permite escribir la integral definida de la función \(h\) como:
Resolviendo cada una de las integrales por separado, obtenemos que: \[\begin{aligned}\int_{1}^{4}2xdx&=2\int_{1}^{4}xdx\\&=2\left(\frac{x^2}{2}\right)\Bigg|_1^4\\&=x^2\Bigg|_1^4\\&=4^2-1^1\\&=16-1\\&=15\end{aligned}\] \[\begin{aligned}\int_{1}^{4}3dx&=3(4-1)\\&=3(3)\\&=9\end{aligned}\]
De tal manera que:
Por lo tanto, la integral definida de \(h(x)=2x+3\) en el intervalo \([1, 4]\) es igual a 24.
Integral definida de una diferencia de funciones
Si \(f\) y \(g\) son funciones integrables en el intervalo \([a, b]\), entonces \(f-g\) es integrable en \([a, b]\) y, además:
Esta propiedad establece que la integral definida de una diferencia de funciones es igual a la diferencia de las integrales definidas de cada función.
Integral definida de una diferencia de funciones ejemplos
Ejemplo 4. Supongamos que queremos hallar la integral definida de la función \(h\) definida como \(h(x)=4x^3-2x^2\) en el intervalo \([1, 3]\). Para simplificar el cálculo, descompondremos la función en la resta de dos funciones más simples. Si \(f(x)=4x^3\) y \(g(x)=2x^2\), entonces: \[\begin{aligned}h(x)&=f(x)-g(x)\\&=4x^3-2x^2\end{aligned}\]
De acuerdo con la propiedad de la integral definida de una diferencia de funciones, podemos calcular la integral definida de la diferencia de dos funciones restando las integrales definidas de cada función por separado, es decir:
Calculando cada integral por separado, obtenemos: \[\begin{aligned}\int_{1}^{3}4x^3dx&=4\left(\frac{x^4}{4}\right)\Big|_{1}^{3}\\&=3^4-1^4\\&=81-1\\&=80\end{aligned}\] \[\begin{aligned}\int_{1}^{3}2x^2dx&=2\left(\frac{x^3}{3}\right)\Big|_{1}^{3}\\&=\frac{2}{3}(3^3-1^3)\\&=\frac{2}{3}27-1\\&=\frac{2}{3}26\\&=\frac{52}{3}\end{aligned}\]
De tal manera que:
Por lo tanto, la integral definida de la función \(h(x)=4x^3-2x^2\) en el intervalo \([1, 3]\) es igual a \(188/3\).
Propiedades de comparación de la integral definida
Propiedad de positividad de la integral definida
Si \(f\) es una función continua y \(f(x)\geq 0\) para toda \(x\) en el intervalo \([a, b]\), entonces:
Esta propiedad establece que si una función \(f(x)\) es no negativa en un intervalo \([a, b]\), entonces la integral definida de \(f(x)\) en ese intervalo es también no negativa. En otras palabras, el área bajo la curva de una función no negativa es siempre no negativa.
Ejemplo 5. Supongamos que tenemos la función \(f\) definida como \(f(x)=x^2\) en el intervalo \([0, 2]\). Queremos calcular la integral definida de \(f(x)\) en ese intervalo, es decir, queremos hallar la siguiente integral definida: \[\int_{0}^{2}x^2dx\]
La propiedad de positividad establece que si la función \(f(x)\) es no negativa en un intervalo, entonces la integral definida de \(f(x)\) en ese intervalo también es no negativa.
Asegurémonos entonces de que la función \(f\) es no negativa: Para cada \(x\) en el intervalo \([0, 2]\), \(x^2\) es no negativa ya que el cuadrado de cualquier número real es siempre mayor o igual a cero, es decir, es no negativo.
Ahora veamos que ocurre con la integral definida: \[\begin{aligned}\int_{0}^{2}x^2dx&=\frac{1}{3}x^3\Big|_{0}^{2}\\&=\frac{1}{3}(2^3-0^3)\\&=\frac{8}{3}\end{aligned}\]
Dado que \(f(x)=x^2\) es no negativa en el intervalo \([0, 2]\), la integral definida también es no negativa. En este caso, el resultado es \( \frac{8}{3} \), que es positivo.
Este ejemplo demuestra la propiedad de positividad de la integral definida y cómo la naturaleza no negativa de la función se refleja en el resultado de la integral definida.
Propiedad de monotonía de las integrales definidas
Si \(f\) y \(g\) son dos funciones continuas y \(f(x)\geq g(x)\) para toda \(x\) en el intervalo \([a, b]\), entonces:
Esta propiedad establece que si una función \(g(x)\) es siempre menor o igual a otra función \(f(x)\) en un intervalo \([a, b]\), entonces la integral definida de \(g(x)\) en ese intervalo es menor o igual a la integral definida de la función \(f(x)\). Esto refleja que, si una función siempre está por debajo de otra, el área bajo la curva de la primera es menor o igual al área bajo la curva de la segunda.
Ejemplo 6. Consideremos dos funciones \(g(x)=x\) y \(f(x)=x^2\) en el intervalo \([0, 2]\). Queremos demostrar la propiedad de monotonía, que establece que si \(g(x)\) es siempre menor o igual a \(f(x)\) en un intervalo, entonces la integral definida de \(g(x)\) en ese intervalo es menor o igual a la integral definida de \(f(x)\).
Veamos primero si se cumple que \(f(x)\geq g(x)\): Para cada valor de \(x\) en el intervalo \([0, 2]\), \(g(x)=x\) es siempre menor o igual a \(f(x)=x^2\) ya que el cuadrado de cualquier número es siempre mayor o igual así mismo.
Ahora veamos que ocurre con las integrales definidas de cada función en el intervalo \([0, 2]\):
\[\begin{aligned}\int_{0}^{2}xdx&=\frac{1}{2}x^2\Big|_{0}^{2}\\&=\frac{1}{2}(2^2-0^2)\\&=2\end{aligned}\]
\[\begin{aligned}\int_{0}^{2}x^2dx&=\frac{1}{3}x^3\Big|_{0}^{2}\\&=\frac{1}{3}(2^3-0^3)\\&=\frac{8}{3}\end{aligned}\]
Comparando los valores de las integrales definidas obtenemos que: \[2\leq\frac{8}{3}\] En este caso, la propiedad de monotonía se cumple, ya que \(g(x)=x\) es siempre menor o igual a \(f(x)=x^2\) en el intervalo \([0, 2]\), y la integral definida de \(g(x)\) es efectivamente menor o igual a la integral definida de \(f(x)\).
Otras propiedades de la integral definida
Si \(f\) es una función integrable en un intervalo cerrado que contiene a los tres puntos \(a\), \(b\) y \(c\), entonces:
Si \(f\) es una función integrable en \([a, b]\), entonces:
Esta propiedad establece que, si los límites de integración son los mismos, la integral es solo una línea y no contiene área, es decir, la integral definida es igual a cero.
Si \(f\) es una función integrable en \([a, b]\), entonces:
Esta propiedad establece que si los límites de integración se invierten, entonces la integral definida cambia de signo.
Propiedades de la integral definida ejercicios resueltos
Ejercicio 1. Utiliza las propiedades básicas de la integral definida para expresar la integral definida de la función \(f(x)=2x^3+4x^2-x\) en el intervalo \(\left[1, 2\right]\) como la suma de tres integrales definidas.
Solución. De acuerdo con las propiedades básicas de la integral definida, la integral definida de una suma o diferencia de funciones es igual a la suma o diferencia de las integrales definidas de cada función por separado. Además, la integral definida de una constante por una función es igual al producto de la constante por la integral definida de la función. Por lo tanto, aplicando estas propiedades a la integral definida de la función dada, tendremos:
Ejercicio 2. Utiliza las propiedades básicas de la integral definida para evaluar la siguiente integral: \[\int_{0}^{1}\left(3x^2+4\right)dx\] Solución: Dado que la integral definida de una suma de funciones es igual a la suma de las integrales definidas de cada función por separado, entonces:
Observa que ahora tenemos una suma de dos integrales definidas. En la primera, podemos aplicar la propiedad de la integral definida de una constante por una función, y para la segunda aplicamos la propiedad de la integral definida de una función constante, de tal manera que obtenemos:
Ejercicio 3. Si para la función \(f(x)\) se cumple que: \[\begin{aligned}\int_{0}^{10}f(x)dx&=17\\\int_{0}^{8}f(x)dx&=12\end{aligned}\] Hallar el valor de la siguiente integral definida: \[\int_{8}^{10}f(x)dx\]
Solución: Observa que se pide hallar la integral de \(f(x)\) en el intervalo \(\left[8, 10\right]\) conociendo el valor de la integral de esta misma función en los intervalos \(\left[0, 10\right]\) y \(\left[0, 8\right]\). Como el intervalo de integración más grande es \(\left[0, 10\right]\), entonces debemos expresar este intervalo como la suma de dos intervalos de integración, es decir:
De tal manera que:
Por lo tanto, la integral definida de \(f(x)\) en el intervalo \([8, 10]\) es igual a 5.
Propiedades de la integral definida ejercicios para practicar
Ejercicio 1. Dada la función \(f(x)=3x^2+2x \) en el intervalo \([1, 3]\), calcula la integral definida \[\int_{1}^{3} f(x)dx\]
Ejercicio 2. Considera las funciones \(g(x)=2x^3\) y \(h(x)=4x^2\) en el intervalo \([0, 2]\). Calcula la suma de las integrales definidas: \[\int_{0}^{2} g(x)dx\] \[\int_{0}^{2} h(x)dx\]
Ejercicio 3. Dada la función \(k(x)=e^x\) en el intervalo \([1, 2]\), verifica si la propiedad de comparación con constantes se cumple para \(k(x)\) y \(M=5\).
Ejercicio 4. Considera las funciones \(p(x)=2x\) y \(q(x)=x^2\) en el intervalo \([0, 2]\). Demuestra la propiedad de monotonía, mostrando que \(p(x)\) es siempre menor o igual a \(q(x)\) en ese intervalo.
Ejercicio 5. Dada la función \(f(x)=x^3\) en el intervalo \([0, 1]\), verifica si la propiedad de positividad se cumple para \(f(x)\).
Ejercicio 6. Considera las funciones \(g(x)=4\) y \(h(x)=2x\) en el intervalo \([1, 3]\). Calcula la resta de las integrales definidas: \[\int_{1}^{3} g(x)dx\] \[\int_{1}^{3} h(x)dx\]
Ejercicio 7. Dada la función \(k(x)=3x^2\) en el intervalo \([1, 4]\), calcula la integral definida: \[\int_{1}^{4}k(x)dx\]
Ejercicio 8. Considera las funciones \(p(x)=e^x\) y \(q(x)=2\) en el intervalo \([0, 2]\). Demuestra la propiedad de linealidad, calculando \[3\int_{0}^{2}p(x)dx+2\int_{0}^{2}q(x)dx\]
Ejercicio 9. Dada la función \(f(x)=2x+1\) en el intervalo \([1, 4]\), verifica si la propiedad de monotonía se cumple para \( f(x)\).
Ejercicio 10. Considera las funciones \(g(x)=x^3\) y \(h(x)=x^2\) en el intervalo \([0, 2]\). Calcula la diferencia entre las integrales definidas: \[\int_{0}^{2} g(x)dx\] \[\int_{0}^{2} h(x)dx\]
Propiedades de la integral definida preguntas frecuentes
¿Qué es la integral definida? La integral definida es un concepto en cálculo integral que representa la acumulación de cantidades a lo largo de un intervalo específico. Se denota por \(\int_{a}^{b} f(x) \,dx\), donde \(f(x)\) es la función que estamos integrando, y \(a\) y \(b\) son los límites inferior y superior del intervalo de integración.
¿Cuál es la interpretación geométrica de la integral definida? La interpretación geométrica más común de la integral definida es que calcula el área bajo la curva de la función \(f(x)\) en el intervalo \([a, b]\). Si \(f(x)\) es no negativa en ese intervalo, la integral definida representa el área encerrada entre la curva y el eje \(x\), limitado por las líneas \(x = a\) y \(x = b\).
¿Cómo se relaciona la integral definida con la acumulación de cantidades? Si \(f(x)\) representa la tasa de cambio de alguna cantidad, la integral definida proporciona la acumulación total de esa cantidad en el intervalo \([a, b]\). En otras palabras, la integral definida puede usarse para determinar la cantidad total acumulada a lo largo del tiempo o de alguna variable independiente.
¿Cuáles son algunas propiedades importantes de la integral definida? Algunas propiedades importantes de la integral definida incluyen la linealidad, la suma o resta de intervalos, la comparación con constantes, la monotonía y la positividad. Estas propiedades facilitan el cálculo y la comprensión de las integrales definidas en diversas situaciones.
¿Cómo se utiliza la propiedad de linealidad en el cálculo de integrales definidas? La propiedad de linealidad establece que:
Esto significa que puedes calcular la integral definida de una combinación lineal de funciones dividiéndola en partes más simples y luego evaluando cada parte por separado.
¿Cómo se aplica la propiedad de comparación con constantes en el cálculo de integrales definidas? La propiedad de comparación con constantes establece que si \(f(x) \leq M\) para todo \(x\) en \([a, b]\), entonces: \[\int_{a}^{b}f(x)dx\leq M(b - a)\] Esto significa que la integral definida de una función acotada por arriba por una constante es menor o igual al área de un rectángulo con base \((b - a)\) y altura \( M \).
¿Qué significa la propiedad de monotonía en el contexto de integrales definidas? La propiedad de monotonía establece que si \(f(x) \leq g(x)\) para todo \(x\) en \([a, b]\), entonces: \[\int_{a}^{b}f(x)dx \leq\int_{a}^{b}g(x)dx\] Esto implica que la integral definida de una función siempre menor o igual a otra función en un intervalo es menor o igual a la integral definida de la segunda función.
¿Cómo se puede usar la integral definida en el contexto de velocidades y posiciones? Si \(f(x)\) representa la velocidad de un objeto en un intervalo \([a, b]\), entonces \(\int_{a}^{b}f(x)dx\) proporciona la posición acumulada del objeto en ese intervalo. Es decir, la integral definida de la velocidad da la posición total del objeto durante el intervalo dado.
¿Cuál es la importancia de la propiedad de positividad en el cálculo de integrales definidas? La propiedad de positividad establece que si \(f(x)\geq 0\) para todo \(x\) en \([a, b]\), entonces: \[\int_{a}^{b} f(x)dx\geq 0\] Esta propiedad es crucial para comprender que la integral definida de una función no negativa siempre es no negativa, lo que tiene implicaciones en términos de áreas bajo la curva.
¿Cómo se pueden utilizar las propiedades de la integral definida para simplificar el cálculo? Las propiedades de la integral definida, como la linealidad y la comparación con constantes, permiten simplificar el cálculo de integrales definidas al dividir problemas complejos en partes más manejables. Estas propiedades proporcionan reglas útiles para abordar diversos escenarios y facilitan el análisis matemático.