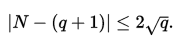代数数论:总集篇
代数数论(一):素理想的扩张
目标:解丢番图方程
什么方程是容易解的?
自然是x^2=y^3这类“某些东西相乘=某个东西相乘”的乘积形式方程,只涉及乘法,只要做质因数分解就不难看出解形如x=n^3,y=n^2
另外,还可以使用模法\mathbb Z \rightarrow \mathbb Z / n \mathbb Z解方程。
然而使用模法和质因数分解的方法对于x^2+2=y^3这类方程失效,一个替代的方法是:
把整数环嵌入一个大的环里面:\mathbb Z \hookrightarrow O_K
然后将加法、乘法都有的方程在大环中化成乘积形式,例如y^3 = x^2+2= (x+\sqrt{-2})(x-\sqrt{-2})\in \mathbb{Z}[\sqrt{-2}]
大环可以是代数整数环,然而其中唯一分解(UFD)不一定成立,但其中素理想仍然成立唯一分解,所谓Dedekind环。
所以进一步求解需要了解素理想,而代数整数环中素理想都是有理素数的提升,因此我们需要研究数域中素理想,方法是考虑域扩张下素理想的扩张:

代数数论(二):素理想分解及一些例子
目标:
①研究方程的解的结构。
②为了能够更好地在大环中操作,需要了解数域中代数整数环自身的结构
最终我们希望把想法上的困难、结构上的困难转换成计算上的困难。
具体计算的方法是:
有限域上分解多项式给出素理想扩张后分解情况
并且我们还讨论了分解域、惯性域,Frobenius同构的作用。
作为例子,我们考虑了二次域、分圆域中素理想分解情况,它们是最常见的数域。
仅利用这些性质,就可以证明二次域都可以嵌入分圆域(Key idea 是小域上分歧的素数一定在大域上分歧!).
以及Gauss著名的二次互反律:
p,q不同奇素数,则\left( \frac{p}{q}\right)\left( \frac{q}{p}\right)=(-1)^{\frac{p-1}{2} \frac{q-1}{2}}
以及二平方和定理:
n为正整数,设n=m^2n_0,n_0无平方因子,那么
n是两个整数的平方和n=x^2+y^2
等价于
n_0没有模4余3的素因子。(并且我们还得到了写成二平方和的方法数)
(一般地,我们还可以解范数型方程N^K_Q(x)=n,x \in O_K)
(二平方和定理的补充可见整数矩阵的平方和问题)
并且利用Chebotarev's density theorem,我们重新得到了Dirichlet密度定理:
任何整数的等差数列an+b, \ \ n=0,1,2,3,\hdots(公差大于0并且a,b互素)含无穷多个素数
代数整数环理论的威力可见一斑。
代数数论(三):单位群、理想类群
目标:研究解的结构、数域的算术结构。
在\mathbb Z的情况下,有唯一分解,单位就是正负1
而一般情况下,唯一分解可能失效(其程度用理想类群刻画),同一个主理想的生成元可能不止差个正负号(也就是说为了从理想回到数,我们必须考虑代数整数环的单位群),这都给解方程带来了困难。
而(三)就是想确定这两者的结构。
利用数的几何中的Minkowski定理(类似抽屉定理的连续推广),我们得到了
(四平方和定理)
任何一个非负整数n都是四个平方数的和。
Dirichlet单位定理
K的单位群U_K是秩为r=r_1+r_2-1的Abel群,从而
U_K \cong W_K \oplus \mathbb Z^r,W_K是K中所有单位根形成的有限群。
类数有限
h_K < + \infty,从而理想类群是一个有限群,其平凡等价于O_K是PID,并且可以如下计算:①计算出判别式等等,从而求出M_K = \left(\frac{4}{\pi}\right)^{r_2} \frac{n!}{n^n}\sqrt{|d_K|}
②考虑使得p\leq M_K的素数p全体,考虑每个p在K中的素理想分解情况
③分解出来那有限多个素理想就生成了整个类群。
④利用范等工具一个一个Check那些素理想是不是主理想,求出它们的作为群中元素的阶。
⑤确定类群大小
(一)(二)(三)基本消除了解方程的所有障碍,在此我们用上面所有方法证明了:
x^2+6=y^3没有整数解
由于这个例子非常典型,所以允许我将证明写下来:
我们有(x+\sqrt{-6})(x-\sqrt{-6})=y^3,问题与数域K=\mathbb Q(\sqrt{-6})有关。
假设有解。
若素理想p|x+\sqrt{-6},p|x-\sqrt{-6},那么p|2\sqrt{-6}
因此要考察理想(2\sqrt{-6})如何拆成素理想:
它的范是24,因此我们只需要考虑2,3在O_K中的素理想分解式。
x^2+6 \ \ in \ \ \mathbb F_2有重根0,所以
同理
3O_K=(3,\sqrt{-6})^2=p_2 ^2所以p|x+\sqrt{-6},p|x-\sqrt{-6},推出p|2\sqrt{-6},推出p=p_1 \ \ or \ \ p_2
如果p=p_1,那么p_1^2|(x+\sqrt{-6})(x-\sqrt{-6})=y^3
所以p_1 |y,所以p_1^3|y^3
又注意到6O_K=2O_K3O_K=p_1^2p_2^2
所以x^2+6=y^3推出(6) \subseteq (y^3)
所以y^3|p_1^2p_2^2,矛盾于p_1^3|y^3
同理
p=p_2也有矛盾,最终我们得到:
(x+\sqrt{-6},x-\sqrt{-6})=1这一点表明(x+\sqrt{-6})(x-\sqrt{-6})=y^3左边是两个互素主理想,从而存在整理想I_1,I_2
使得(x+\sqrt{-6})=I_1^3 ,(x-\sqrt{-6})=I_2^3
从而在类群中I_i,i=1,2的阶都整除3.
注意到h_K=2(类群实际上由[p_1]生成2阶循环群,可以用Minkowski常数算出)
所以由我们上面的观察,那么I_i,i=1,2都是主理想(2、3互素)
又O_K=\mathbb Z[\sqrt{-6}]
从而可设(x+\sqrt{-6})=(a+b\sqrt{-6})^3,a,b \in \mathbb Z
注意K中单位只有正负1,所以我们有
x+\sqrt{-6}=(a+b\sqrt{-6})^3,a,b \in \mathbb Z(两者差一个单位正负1,适当修改a,b符号使等式成立)
比较系数有
x=a^3-18ab^21=-6b^3+3a^2b=3b(-2b^2+a^2)
第二个方程右边是3的倍数,而1不是3的倍数,无解,矛盾!
从而原方程无解。
可见我们已经初步把问题转换为研究数域的结构,特别是求出类数,自然工具越多越好,为此引入解析方法。
不过更一般地,我们还要考虑无穷素理想,这时候把素理想用位的语言表示更方便(素理想就是有限位,阿基米德赋值就是无穷位)
这个最基本的讨论可见域上的绝对值与Ostrowski定理。
关于位的完备化,就将我们引向local field.
代数数论(四):类数公式
目标:解析方法
引入了数论函数和形式D级数,讨论了它们的关系,最终发现数论函数大多与zeta函数有关,为此转而研究zeta函数,证明了
\zeta(s)=\sum_{n=1}^{\infty}{\frac{1}{n^s}} 在右半平面\ \ Re \ \ s > 1解析,并且可以解析延拓(注意\ \ Re \ \ s > 1外的地方原来的级数表达式不能够再使用)到复平面上成为亚纯函数,只有一个单极点1,留数为1.
并且其还有一个函数方程:
\xi \left( s\right) =\Gamma \left( \frac{s}{2}+1 \right) \left( s-1\right)\pi ^{-\frac{s}{2} } \zeta \left( s \right)那么\xi(1-s)=\xi(s)
还可以考虑推广上述定义,例如
Dirichlet L函数:
设\chi :(\mathbb Z/n\mathbb Z)^\times \rightarrow \mathbb C为一特征标,其自然延拓到全体整数,称为Dirichlet特征,定义
L(s,\chi )=\sum_{n=1}^{\infty}{\frac{\chi(n)}{n^s}}任一数域K的zeta函数:
\zeta_K(s)=\sum_{0 \ne I\subset O_K ideal }^{} {\frac{1}{N(I)^s}}可以证明它们也可以延拓到复平面上的亚纯函数,同理也应该有一个函数方程用于延拓。
并且有:
(类数公式)
res_{s=1}\zeta_K(s)=h_Kres_{s=1}\zeta_K(C,s)=\frac{2^{r_1}(2\pi)^{r_2}R_Kh_K}{w_K\sqrt{|d_K|}}
(R_K是证明单位定理是把单位群嵌入到超平面得到格的投影面积,称为正规子(regulator),这通常很难求,因为基本单位难求)
(w_K是单位根群的阶,即K中单位根数量,当K为实域时,单位根只有1、-1,为2)
为此要求类数,只要求出留数和正规子(其他如判别式都是可求的)
进一步有具体的类数公式:
K为虚二次域\mathbb Q(\sqrt{d}),d<0,且d不等于-1,-3(这两者情况类数都是1)
则
h_K=\frac{1}{|d
_K|}|\sum_{k=1}^{|d_K|}{k\chi_K(k)}| =\frac{1}{2-\chi_K(2)}|\sum_{1 \leq k<\frac{|d_K|}{2}}^{}{\chi_K(k)}|
K为实二次域\mathbb Q(\sqrt{d}),d>1,设其一基本单位为\varepsilon >1
则
h_K=\frac{1}{log \varepsilon }|\sum_{1 \leq k<\frac{|d_K|}{2}}^{}{\chi_K(k)}log( sin\frac{\pi k}{|d_K|})|
而且解析方法可以用来证明一大堆密度定理(无穷多个),方法是用特征的正交关系分离我们想要的东西,化成一个整体求和,然后分段进行估计,这种思路是指数和方法的渊薮。
代数数论(4.1):zeta function’s simple pole
代数数论(四):类数公式的补完,补充了zeta函数在s=1处为单极点,且留数为1的证明。
代数数论(4.2):modular form and sum of squares
解析方法的继续
我们简单介绍了模形式这一有力工具,其有两大特点——刚性,可构造性。
这让我们可以证明上面提到过的二平方和与四平方和定理,甚至可以证明三平方和和八平方和定理。
为了证明模性,我们用到了著名的Poisson Summation:

再次把技术上的困难转换成了计算上的困难(用到了复分析中余切函数的展开公式,估计余项判定绝对收敛等等)
代数数论(4.3):简单的丢番图逼近
解析方法的继续
我们证明了一些简单的丢番图逼近的定理,这种思想将在Siegel theorem——数域上椭圆曲线上整点有限的证明中起到作用。
(Dirichlet)
\alpha \in \mathbb R - \mathbb Q,则存在无穷多个有理数\frac{p}{q},使得
( Liouville )
\alpha \in \bar{ \mathbb Q}为代数数,并且不是有理数.
那么存在依赖于\alpha \in \bar{ \mathbb Q}的常数C>0,使得对任何有理数\frac{p}{q}有:
|\alpha -\frac{p}{q}| \geq \frac{C}{q^d}其中d是\alpha \in \bar{ \mathbb Q}的次数(即极小多项式的次数)
所以如果一个数的小数点后太多0,那么这个数一定不是代数数,刘维尔就用这个想法构造出了第一个明确已知的超越数:
a=\sum_{n=1}^{\infty}{\frac{1}{10^{n!}}}代数数论(4.4):Tate's thesis
解析方法的继续
\zeta(s)=\sum_{n=1}^{\infty}{\frac{1}{n^s}} =\prod_{1}^{\infty}\frac{1}{1-\frac{1}{p^s}} 的解析延拓,
最后得到的对称函数方程是关于Z \left( s\right) =\Gamma \left( \frac{s}{2} \right) \pi ^{-\frac{s}{2} } \zeta \left( s \right) 的:Z(s)=Z(1-s)
令\Gamma \left( \frac{s}{2} \right) \pi ^{-\frac{s}{2} } :=Z_\infty(s)
那么
Z \left( s\right) =\Gamma \left( \frac{s}{2} \right) \pi ^{-\frac{s}{2} } \zeta \left( s \right) =\prod_{p\leq \infty}^{} Z_p(s)应该很容易发现:
右边的乘积与\mathbb Q的所有位(素数,无穷位)一一对应
自然猜想:
Z_p(s)其实来自于局部域\mathbb Q_p,可以看成是一个局部的zeta函数,而它们全部拼起来就成了整体的zeta函数,而位的自对偶性给出整体对称。
进一步我们算出:
Z_p(s)=\int_{ \mathbb Z_p}^{} |x|^s \frac{dx}{|x|}=\int_{ \mathbb Q_p^{\times}}^{}1_{\mathbb Z_p}(x) |x|^s \frac{dx}{|x|}Z_\infty(s)=\int_{\mathbb R^{\times}}^{}e^{-\pi x^2} |x|^s \frac{dx}{|x|}
为了研究透彻每个zeta function怎么来的,我们需要更多local field的知识,具体来说就是tate thesis 所做的:
①先在每个local field的加法群、乘法群(分别都是局部紧拓扑群)上定义测度,积分,fourier变换,速降函数空间,证明它们都是自对偶的(Pontryagin duality是自己,并且由典范的特征给出同构),再得到Fourier反演公式。
然后利用local field加法群、乘法群的quasi-特征标(即到复数乘法群的连续同态)定义local zeta function 和 local L series,证明前者有函数方程,函数方程中的\varepsilon factor可以计算出来.
②把上面的local信息整体拼成Adele与idele上的信息(测度、积分、fourie变换等等),得到了Adele也是自对偶的等等,利用Hecke特征标定义Global zeta function.
③建立Adele 上Poisson summation formula,其中顺便还用到了product formula以及典范特征在K上平凡等等性质,然后利用这个以及local 的方程,得到整体zeta function的方程.
最简单例子:

显然可以从中看出s与1-s,f与f的fourier变换的对称性,即
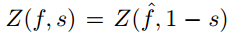
展开成local product两边数留数就得到了计算留数公式。
到③就完成了1,2,例如取平凡特征标就是上面的Dedekind zeta函数方程等等...而3也类似,估计Global zeta function化为对每个local 项的估计。
并且其实很多时候对于一般数域K要做的事情我们只需要对Q验证,因为:
\mathbb A_K \cong \mathbb A_{\mathbb Q} \otimes_{\mathbb Q} K,而K上的自对偶同构来自于Q上的自对偶同构取Trace.
所以大大简化了证明.
另外可参见基本的关于黎曼猜想的介绍:
从巴塞尔问题到黎曼\zeta函数(0):A conclusion named after Legendre
从巴塞尔问题到黎曼\zeta函数(1):巴塞尔问题以及其推广:\zeta(x),x为整数(前篇)
从巴塞尔问题到黎曼\zeta函数(2):巴塞尔问题以及其推广:\zeta(x),x为整数(后篇)
从巴塞尔问题到黎曼\zeta函数(完结篇):黎曼猜想:黎曼的开拓与他留给后人的挑战
代数数论(4.5): 阿黛尔与伊代尔
(4.4)中出现的local field, adele, idele 等等 object的介绍。
数域上会有所有位,所以称为global field;
两者自然有很多联系,联系的中间人就是adele与idele;
而Hasse的局部整体原理也反映了这点。
代数数论(五):解方程
目标:从范畴论和scheme的观点来看解方程
我们已经知道y^3=x^2+6没有整数解,如何求解Pell方程,什么整数能写成二、四平方和等等结论。
就如许多PDE没有显式解一样,寻求万有之法解决所有丢番图方程的求解是一个很奢侈的要求(算法上不可确定的)
而在之前求解过程中我们已经发现在解方程之前搞清楚数域的代数整数环、类群、单位群是很有用的,所以应把目标先转向研究数域的算术结构、方程本身的结构,还有有没有解、有多少解这种定性的问题。
有一个整系数多项式f \in \mathbb Z[x_1,\hdots,x_n],我们想求解f=0的整数解、有理数解、模p的解…
换句话说,我们希望求解
f(x_1,\hdots,x_n)=0 ,x_i \in R其中R是一个交换幺环,通常例子有\mathbb Z ,\mathbb Z / p^k\mathbb Z(p素数,k正整数),\mathbb Q,\mathbb R\mathbb C等等
记Z(f)(R)为f(x_1,\hdots,x_n)=0 ,x_i \in R的全体点(x_1,\hdots,x_n)构成的集合,我们的问题就是:
对于一些数论中感兴趣的环R,了解Z(f)(R)。
上面其实得到了一个函子:
Z(f): \bf{Ring} \rightarrow Set进一步可参见:
代数数论(六):椭圆曲线
我们希望在
\mathbb Q以及数域等整体域,\mathbb R,\mathbb C,\mathbb Q_p等局部域,\mathbb Z/p\mathbb Z等有限域这三种域上解方程,同时我们还希望考虑\mathbb Z或其他代数整数环中的解即整点问题。
而方程的解如果带有群结构,那么就好处理很多,这就引入了椭圆曲线。
域k(特征0)上的椭圆曲线可以看成由下面式子定义的点全体再加上一个无穷远点:
y^2=x^3+ax+b,(x,y) \in k^2,a,b为k中常数
要求右边判别式\Delta =-16(4a^{3}+27b^{2})不等于0(即无重根,为了保持光滑性,没有cusp),其上的点可以自然地有一个群结构(实数域为例):


然后我们考察了许多例子:
y^3=x^2+6没有整数解;
高度;
著名的同余数问题以及BSD猜想;
(\frac{4381019}{4989780}, \frac{9226981}{4989780}) is a solution for x^3+y^3=7;
具体求解,例如证明
y^2 = x^3 +n对于n=-3,-6,-9,-12,-24,6,45,46都没有整数解;
Fermat 大定理;
最后我们罗列了一堆重要定理:
(Mordell-Weil,1922)
Q上的椭圆曲线E的有理点E(\mathbb Q)是有限生成Abel群:
E(\mathbb Q)=\mathbb Z^r \oplus T,
T是挠点全体,为有限Abel群,r称为E的秩
(Mazur,1977)
上面的T只可能为:
\mathbb Z/ N\mathbb Z ,其中N = 1, 2, ..., 10, or 12,
或 \mathbb Z/2\mathbb Z \times \mathbb Z/2N\mathbb Z 其中 N = 1, 2, 3, 4
这15个群之一
(Siegel,1929)
Q上的椭圆曲线E的整点(坐标均为整数的点),或者更一般的坐标有一者为整数的点,只有有限个。
(Hasse)
If N is the number of points on the elliptic curve E over a finite field with q elements, then
代数数论(七):立方数之和


讨论了Ramanujan的taxicab number,例如:
1729是最小的能恰好用两种方式写成两个立方数之和的正整数。
并且探讨了立方数之和与平方和表示的区别,以及与椭圆曲线的联系。
代数数论(7.5):二次型与整数表示

补充之前没提到的许多二次型表示整数的结果,
包括Hasse-Minkowski定理,Conway的15 theorem,Manjul Bhargava的290 theorem
代数数论(八):Hilbert 94 and class field theory
用群的上同调的观点(一套长正合列)来重新得到Hilbert 94,并且引入Hilbert class field.
并且我们表明,class field theory就是寻找etale fundamental group of arithmetic scheme的内蕴刻画。
代数数论(8.5):More about hilbert class field
利用hilbert class field的存在性,我们可以证明很多有用的关于类数的结论,例如
①L/K有限扩张,那么H_KL \subseteq H_L;
②如果数域L类数为1,那么必须H_K \subseteq L,对L的任何子域K;
③L/K有限扩张,如果
(1)[L:K]与h_K互素
(2)存在一个K中素理想p(或者无穷位v)在L中完全分歧
有一者发生,那么
h_K | h_L④记\mathbb Q(\zeta_{p^n})类数为h_n,则h_n |h_{n+1}
代数数论(九):local class field theory
local class field theory
Why local first?
Finite field is simple than Local field
Local field is simpler than Global field
我们时刻类比有限域和local field(非阿,特征0)
如果F是有限域,那么成立:
①解方程可以直接枚举解
②F^{\times}的结构就是一个有限循环群
③n次Galois扩张的Galois群一定是循环群
④F的n次扩张只有一个
⑤Galois上同调直接转成\hat{\mathbb Z}的上同调,通常转为循环群的上同调(此时模2周期性)
如果F非阿局部域,且特征是0,那么对应稍复杂的性质成立:
①Hensel lemma成立,解方程约等于在有限域中解
②F^{\times}虽然不是循环群,但结构完全知道:

\mathbb Q_p^{\times} = \mathbb Z \times \mathbb Z/(p-1) \mathbb Z \times \mathbb Z_p \ \ (p >2)
\mathbb Q_2^{\times} = \mathbb Z \times \mathbb Z/2 \mathbb Z \times \mathbb Z_2
F^{\times} / (F^{\times} )^n有限Abel群
③K/F n 次 Galois扩张,则Gal(K/F) 一定是可解群。
④F的n次扩张只有有限个
⑤F的Galois上同调很简单。
有限域最简单,此时我们有类域论:
设F是一个有限域,我们有自然的映射
\mathbb Z \rightarrow Gal(F^{ab}/F) :
n \rightarrow \sigma^n
\sigma 是F的Frobenius自同构
①
profinite completion后上面是同构,这给出F的有限Abel扩张与Z的有限指标开子群一一对应
②
函子性:有限域的n次abel扩张,则Z自乘n倍的映射给出两个自然映射交换图表
③
我们可以显式构造出所有F的n次Abel扩张
现在回到local field class theory,其表述为:
假设F是一个local field,则
有自然的映射F^{\times} \rightarrow Gal(F^{ab}/F)
①
profinite completion后上面是同构,这给出F的有限Abel扩张与F^{\times}的有限指标开子群一一对应,具体对应为:
E/F n 次 abel扩张 对应于开子群N_{E/F}E^{\times}
并且Gal(E/F) \cong F^{\times} /N_{E/F}E^{\times}
②
函子性:E/F n次abel扩张,则E到F的取范映射给出两个自然映射交换图表
③
explicit class field theory 可见
而local class field theory的证明,可以参见neukirch《 algebraic number theory》
作为应用,我们求出了:
\mathbb Q_p 的q次Galois扩张只有有限个,其个数为
①p>2:
q+1 (若q|p-1或q=p),1(else)
②p=2:
7(q=2),1(else)
代数数论(十):Global class field theory
class field theory可以看成寻找arithmetic scheme的基本群的内在刻画,因此可以看成是Galois theory for number field的进一步加强。
至于Global class field theory ,其可用local case所得到,具体来说是因为idele是local field的restrict product,因此idele的取范映射就是local field的取范的复合,而整体Galois扩张又诱导每个位上的Galois扩张。
idele group是集local于一体的对象,单独来看并没有反映整体的信息,但数域也可以嵌入idele和adele中,因此其包含了整体的对象。
而idele class groupC_K= \mathbb I_K /K^{\times}是把局部的对象整合起来商掉一个整体的关系,因此其能反映local information 如何通过global field 联系,因此可用来描述整体信息。
上面说了一堆废话,Global class field theory就是说:
number field K的有限Abel扩张 与 C_K= \mathbb I_K /K^{\times}的有限指标的开子群一一反序对应,具体对应为:
E/K对应N_{L/K}C_L,且Gal(E/K) \cong C_K/N_{L/K}C_L
并且Global与local的类域论可以通过local field 嵌入 idele group 联系起来,其可以用来反映数域的分歧情况。
作为应用有:
Kronecker–Weber theorem
任何一个Q的Abel扩张都是某个分圆域的子域
就是这样,我们回顾了从开始到1950年左右的代数数论知识(bi)
感谢各位的支持,由于最近琐事较多(加上期末考试临近),因此停止更新一段时间(当然欢迎投稿),假期再见!