抽象代数教学体系的探索 I

扬州大学的李立斌老师联系我说要开一个抽象代数教学研讨会, 希望我去给个报告谈谈教学体会. 我实话实说: 没有完整教过这一课程, 做的一些思考, 以及在公众号里写的相关文章, 大部分是在我带一些大一、大二学生玩抽象代数的过程中产生的, 属于自娱自乐. 李老师就让我讲讲怎么跟学生玩的.

2020 年 12 月 18 日, 我应邀来到扬州大学, 谈了自己对抽象代数及相关课程体系的思考, 现在把所谈的内容整理成文字. 我必须得说明: 我的想法的确是基于一些实践, 出发点是引导学生们去自发探索抽象代数的内容, 但愿意跟我一起探索的大一、大二学生一般不超过十人, 因此我所做的探索是小众的, 样本很少, 没有统计学上的意义; 另外, 我的思考是立足于代数学的整体思考, 对大多数将来不做数学研究的学生未必适用, 他们或许可以从中得到一些启发, 知道一些问题的来龙去脉, 从而解答一些疑惑. 因此, 以下思考仅供参考.

整体思路

我对抽象代数课程的定位是“承前启后”, 也就是说, 它在代数学课程体系中起到纽带的作用. 一方面, 抽象代数中的很多概念都来源于高等代数或者是用高等代数处理问题的过程中产生的; 另一方面, 抽象的思维方式可以让我们更高效地处理有共性的问题, 提炼出有用概念——数学的确是玩概念的, 进而发展称各种深刻的数学分支.

当然, 抽象代数自身有很多问题值得研究, 比如有限单群的分类. 但这些深刻的问题一般不是仅仅靠抽象代数自身来解决的, 需要和其他数学分支包括高等代数进行融合.然而, 传统的抽象代数教学偏重于对群、环、域等抽象概念的介绍, 与之前的高等代数及之后的表示论等内容的脱节比较严重, 也可能非常严重. 比如一个很普遍的问题是, 很多学生知道群、环、域的概念, 但是举不出有意思的例子, 而这些例子往往就存在于高等代数之中, 学生甚至老师都有意无意地忽略了这一点.

问题是怎么把抽象代数和前后的课程融合在一起呢?

首先, (有理系数)方程求根本质上考虑包含方程所有根的最小数域 {\mathbb E}, 这是 {\mathbb Q} 上的有限维线性空间, 方程根式解的问题转化为 {\mathbb E} 的结构问题——根式扩张. 这部分只需要高等代数中的数域、多项式和线性空间理论.

其次, 天才的 Galois 发现研究 {\mathbb E} 的结构可转化成另一个问题, 用现代的语言来说就是利用线性变换 \operatorname{End}_{\mathbb Q}{\mathbb E}, 尤其是其中保持 {\mathbb E} 中乘法的非零线性变换的集合 G (Galois 群). 对 G 的研究就自然引入了群, 这是群论的任务.

第三, 完成群论的基础研究, 再回到方程求根的判别上来, 并把相关理论推广到一般域上, 这就是 Galois 理论.

第四, 对群论的深入研究的最大功臣是高等代数(有点意外?), 从而发展为表示论, 也就是把抽象的群实现为具体的矩阵群, 并考虑所有不同的实现方式. 这大概类似于医学中对人体做各个方向的扫描, 然后合成得到整体信息. 有趣的是, 这里又蕴含了群论与 Lie 代数的联系.

这些观点可以用一张图来表示:

这个过程是“螺旋式的上升”: 从高等代数出发研究域论, 再发展出群论, 从而彻底解决方程根式解, 然后回到高等代数来研究群论. 学生们经过这样的洗礼不仅能对域和群的抽象理论有深刻的理解, 在使用过程中也会对高等代数的把握上一个层次, 达到高等代数、域论、群论和有限群表示论的融合.

环论和模论是另外一个故事, 但与群论和域论有紧密关联. 我们依然可以从高等代数入手, 即以整数和多项式的因式分解为出发点, 探讨一般代数整数的因式分解, 由此自然引出 Euclid 环、主理想整环和唯一析因环等环论的一般理论, 这里有大量的代数整数环的例子作为支撑. 建立不同环之间联系的是环同态, 特别地, 将一般环实现成具体的变换(矩阵)就是模论, 这类似与群作用与群表示. 高等代数中处理 Jordan 标准形的方法之一是多项式矩阵, 这就是模论的雏形.

尺规作图

很多抽象代数书中都会提到尺规作图, 这是抽象理论对于古典问题的精彩回答. 不过, 需要说明的是, 著名的古希腊三大尺规作图问题的解决并不需要抽象代数, 核心思想是线性空间!

问题 1 (1) 平面上所有能用尺规作图得到的点(对应于复数)构成一个数域.

(2) 设 {\mathbb F}\subseteq {\mathbb E} 为数域, 则 {\mathbb E} 为 {\mathbb F} 上的线性空间.

(3) 设 {\mathbb F}\subseteq {\mathbb K}\subseteq {\mathbb E} 为数域, 则 \dim_{\mathbb F}{\mathbb E}=\dim_{\mathbb K}{\mathbb E}\cdot\dim_{\mathbb F}{\mathbb K}.\\

(4) 若从单位长度出发, 平面上点 a 可经过有限步尺规作图得到, 则存在数域 {\mathbb E} 使得 a\in{\mathbb E} 且 \dim_{\mathbb Q}{\mathbb E}=2^n.

(5) 三等分任意角、倍立方问题不可能实现: 包含 \sqrt[3]{2} 或 \cos 20^\circ 的最小数域是 {\mathbb Q} 上的三维线性空间.

(6) 化圆为方不能实现: 需要 \pi 是超越数.

不过有的尺规作图问题是高等代数解决不了的, 例如正 n 边形作图. Gauss 的杰作之一是正 17 边形的作图, 实际上他得到了

\cos\dfrac{2\pi}{17} =-\dfrac{1}{16} + \dfrac{1}{16} \sqrt{17} + \dfrac{1}{16} \sqrt{34 - 2 \sqrt{17}} \\\hspace{4cm}+\dfrac{1}{8} \sqrt{ 17 + 3 \sqrt{17} - \sqrt{34 - 2 \sqrt{17}} - 2 \sqrt{34 + 2 \sqrt{17}} } \\

有了上述公式, 自然可以得到正 17 边形的作图方法——如果纸、直尺、圆规都充分大的话. 若要在一张小小的 A4 纸上实现, 就需要找更好的方法, 这难不倒 Gauss.

这里有个问题: Gauss 是怎么计算出 \cos\dfrac{2\pi}{17} 的? 他的方法能够推广求一般的 \cos\dfrac{2\pi}{n}, 从而实现一般正 n 边形的尺规作图? 结论很神奇, 竟然与著名的 Fermat 素数有关系:

问题 2 设 \theta\in{\mathbb C} 为 n 次本原单位根, 则下列结论等价:

(1) 尺规作图可以作出正 n 边形;

(2) \dim_{\mathbb Q}{\mathbb Q}(\theta) 是 2 的幂次, 其中 {\mathbb Q}(\theta) 是包含 \theta 的最小数域;

(3) n=2^kp_1\cdots p_l, 其中 k\in{\mathbb N}, p_1,\cdots,p_l 为互不相同的 Fermat 素数, 即形如 2^{2^m}+1 的素数.

上述问题的解决需要 Galois 理论.

从高等代数出发的 Galois 理论初步

一般抽象代数课程都是从群论开始介绍各种抽象名词, 高度的抽象性令很多初学者望而却步. 经常听到这样的争议: 群论的很多概念, 如正规子群、可解群等, 都有一个略显奇怪的名词——至少对初学者而言, 这些东西很难记住, 要想知道其来历需要等到学习 Galois 理论时, 那时只有一个小问题——群论知识都被忘得差不过了, 需要老师重新回顾一下, 有时可能耗时很久也达不到效果. 这两部分内容到底该怎么协调?

其实历史本身已经给了答案: Galois 是在研究方程根式解的过程中发展出群的各种概念和性质的, 而经过一代代数学家的努力, 我们已经可以把 Galois 最初的比较晦涩的思路整理得非常清晰, 其中的主要工具竟然就是高等代数! 因此先从高等代数角度介绍一些方程根式解的基本思想或许是个有益的尝试.

首先, 需要把数域 {\mathbb F}_0 (如有理数域)上的方程求根转化为一个数域问题.

问题 3 设 f(x)\in{\mathbb F}_0[x] 的所有复根为 \alpha_1,\alpha_2,\cdots,\alpha_n.

(1) 包含 \alpha_1 的最小数域为

{\mathbb F}_1={\mathbb Q}(\alpha_1)=\{a_0+a_1\alpha_1+\cdots+a_{n_1-1}\alpha_1^{n_1-1}|a_i\in{\mathbb Q}\}, \\

其中 n_1=\dim_{\mathbb Q}{\mathbb F}_1=\deg f_1(x), f_1(x)\in{\mathbb Q}[x] 为 \alpha_1 的最小多项式(即以 \alpha_1 为根的首一不可约多项式).

(2) 包含 {\mathbb F}_1 和 \alpha_2 的最小数域为 {\mathbb F}_2={\mathbb F}_1(\alpha_2), 则 \dim_{{\mathbb F}_1}{\mathbb F}_2=\deg f_2(x), 其中 f_2(x)\in{\mathbb F}_1[x] 为 \alpha_2 的最小多项式.

(3) 包含 f(x) 的所有根的最小数域(分裂域)为

{\mathbb E}={\mathbb F}_n={\mathbb F}_{n-1}(\alpha_n)(={\mathbb F}_{n-1}),\ \ \ \dim_{\mathbb Q}{\mathbb E}\leq n!. \\

其次, 用数域来描述方程根式解.

问题 4 以正十七边形(即求 x^{17}=1 的根)为例:

(1) {\mathbb F}_1={\mathbb Q}(\sqrt{17}): {\mathbb Q} 上添加 \sqrt{17};

(2) {\mathbb F}_2: 在 {\mathbb F}_1 上添加 \sqrt{34+2\sqrt{17}}, 这个数域中包含了 \sqrt{34-2\sqrt{17}};

(3) {\mathbb F}_3: 在 {\mathbb F}_2 上添加

\sqrt{ 17 + 3 \sqrt{17} - \sqrt{34 - 2 \sqrt{17}} - 2 \sqrt{34 + 2 \sqrt{17}} }. \\

(4) 得到数域列 {\mathbb Q}={\mathbb F}_0\subseteq{\mathbb F}_1\subseteq{\mathbb F}_2\subseteq{\mathbb F}_3, 其中

\cos\dfrac{2\pi}{17}\in{\mathbb F}_3. \\

这里涉及的数域都是在小的数域上添加一个根式 \alpha 得到的, 自然是比较特殊的数域. 根式 \alpha 的严格描述是 \alpha^n 属于小的数域. 于是, 我们称方程 f(x)\in{\mathbb F}[x] 可用根式解实际上就是要求一个数域列

{\mathbb F}={\mathbb F}_0\subseteq{\mathbb F}_1\subseteq\cdots\subseteq{\mathbb F}_n, \\

其中 {\mathbb F}_i 是在 {\mathbb F}_{i-1} 中添加 \alpha_i (\alpha_i^n\in{\mathbb F}_{i-1}) 得到的, 使得 f(x) 的所有根都在 {\mathbb F}_n 中. 为了方便, 我们把上述数域列称为根式扩张塔.

第三, 用新的方法描述根式扩张塔, 或者更一般地, 描述任何数域.

这是天才的 Galois 的发现. 根据一代代数学家的努力, 现在已经可以用非常简单的语言来描述这一发现, 关键的工具是还是来源于高等代数——线性空间和线性变换.

问题 5 (1) 设 {\mathbb F}\subseteq{\mathbb E} 都是数域, 则 {\mathbb E} 是 {\mathbb F} 上的线性空间;

(2) 记 \operatorname{End}_{\mathbb F}({\mathbb E}) 为线性变换的全体,

G^*=\{\varphi\in\operatorname{End}_{\mathbb F}({\mathbb E})|\varphi(ab)=\varphi(a)\varphi(b),\forall a,b\in{\mathbb E}\}, \\

则 0\in G^*, 非零 \varphi 都是单射;

(3) 令 G=G^*\setminus\{0\}, 当 \dim_{\mathbb F}{\mathbb E}<\infty, G 中元素都是同构, 且 \operatorname{id}\in G, 若 \sigma,\tau\in G, 则 \sigma^{-1},\sigma\tau\in G.

这就是说, G 在乘法和求逆运算下是封闭的, 用行话来说, G 是一个群, 称为 {\mathbb E}/{\mathbb F} 的 Galois 群.

第四, {\mathbb E}/{\mathbb F} 的 Galois 群的结构.

如果尝试计算不同数域 {\mathbb E}/{\mathbb F} 的 Galois 群 G, 我们不难发现

问题 6 若 \dim_{\mathbb F}{\mathbb E} 是有限的, 则 G 是有限集.

实际上, Dedekind 得到了更强的结论, 用到的工具还是高等代数——齐次线性方程组求解和线性相关性.

问题 7 (Dedekind 无关性定理) |G|\leq\dim_{\mathbb F}{\mathbb E}.

一个自然(?)的问题是: 等号何时成立? 结论是惊人的!

问题 8 (困难!) 等号成立当且仅当 {\mathbb E} 是某个多项式 f(x)\in{\mathbb F}[x] 的分裂域.

这就把方程求根问题与其分裂域的 Galois 群的结构完美地联系起来了. 于是终结问题是:

问题 9 根式扩张塔的 Galois 群有什么非同寻常的特点?

由此引出可解群的概念及群论的很多研究. 详见数林广记: 《给大一学生的 Galois 理论》.

群论的研究思路

方程根式解的问题把群论的研究推上了历史舞台, 由此打开了一道通向美妙的抽象数学理论的大门, 代数学理论的研究从此走上了快车道.

要研究一个新的数学对象, 首先要找到找到足够多同类型的例子. 实际上, 历史上的很多数学研究都隐含了群的踪迹, 例如初等数论中不超过正整数 n 且与 n 互素的正整数全体(涉及 Fermat 小定理、Wilson 定理和 Euler 定理等), Mobius 反演公式, Vandermonde 和 Lagrange 等人对方程的根的对称性的研究, 可逆矩阵及正交矩阵的全体, 几何体的对称性例如三维空间的等距变换等, 这些都推动数学家们把群作为一个独立的分支来研究.

其次, 面对众多的研究对象, 需要研究它们之间的关系, 这就要考虑映射, 这样的映射(群同态)必须要保持群的乘法运算, 否则就破坏了群的结构. 群同态的核与像自然是重点关注对象, 尤其是前者, 因为核具有非常好的结构特点. 这样, 正规子群和商群就自然产生了. 这个过程类似于求整数或多项式的因式分解、线性空间的子空间与商空间, 对于群就是要把它表示成正规子群和商群的合成(群扩张).

第三, 如果继续对正规子群和商群做类似分解, 就能得到更小的群. 对于有限群而言, 这个过程有限步后会终止, 从而得到一些不能再分解的群(即单群). Jordan-H"{o}lder 定理表面, 最后得到的单群与分解过程无关, 即任何有限群总是有固定的单群扩张得到, 当然扩张过程有很多种, 从而得到不同的群.

第四, 在扩张的意义下, 群论归结为研究有限单群, 也就是要判断非平凡正规子群是否存在, 或者等价地, 是否存在非单也不平凡的群同态 \varphi:G\rightarrow H? 这样的 H 必须是一个比较具体的群, 否则不方便研究 \varphi, 一个自然的选择是集合 X 的置换群 S_X, 从而需要考虑群 G 在集合 X 上的作用. 这是群论中非常精彩的地方. 当然, X 的选择有很多种, 这一点在著名的 Sylow 三定理的研究中体现得非常明显.

第五, 特别要指出的是, 利用素数阶群扩张得到的群就是可解群, 由此可以回到方程根式解的问题中完成临门一脚, 证明方程可用根式解等价于其分裂域的 Galois 群是可解的. 而很多群是不可解的, 例如 S_n,A_n (n\geq 5), 可以构造一些方程使得其分裂域的 Galois 群就是 S_n, 从而五次以上的方程未必有用根式解, 圆满解决这一长期困扰数学界的难题.

至此, 域论和群论形成了一个完美的轮回. (详见: 数林广记: 《问题引导的抽象代数》)

群论与表示论

当考虑群 G 在集合上的作用时, 如果所考虑的集合是一个线性空间 V, 则我们自然会考虑 G 在 V 上的线性作用. 也就是说, 我们不考虑 G 到 S_V 的群同态, 而是考虑 G 到可逆线性变换的全体(一般线性群) \operatorname{GL}(V) 的群同态.

尽管我们在高等代数课程中对线性变换做了长期研究, 但在一般抽象代数课程中, 线性变换仅有的出场机会是把 \operatorname{GL}(V) 作为一个微不足道的群的例子. 然而出人意料的是, 有限单群的分类理论的最大功臣是 \operatorname{GL}(V), 即把抽象的群实现为具体的线性变换或矩阵群, 并要考虑所有本质上不同的实现方式, 这就是表示理论——大概类似于医学中对人体做各个方向的扫描, 然后合成得到整体信息. 这个过程是“螺旋式的上升”: 从高等代数出发研究域论, 然后发展出群论, 又回到高等代数来研究群论. 学生们经过这样的洗礼不仅能对域和群的抽象理论有深刻的理解, 在使用过程中也会对高等代数的把握上一个层次, 达到高等代数、域论、群论和有限群表示论的融合.

当 Frobenius 用高等代数的相关内容来研究群的时候, 包括 Burnside 在内的数学家们对此是不屑一顾的, 只不过 Frobenius 很快用丰硕的成果改造了他们. 有限群表示论的研究思路与前文谈到的群论的研究思路如出一辙, 在此不赘述, 我们仅举一例.

问题 10 (1) 正十二面体的旋转对称群同构于最小的非交换单群 A_5. 这一点从下图能看出来——如果你能看到其中有五个正方体, 并且看到 A_5 在这五个正方体上的可递作用.

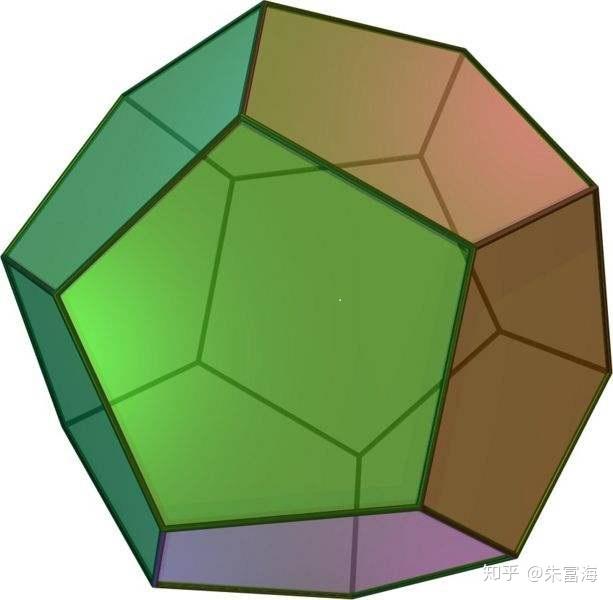
(2) 上述作用得到了 A_5 的一个五维表示.

(3) A_5 在正十二面体的六条对角线上的作用是可递的, 这是独一无二的, 其他 A_n 在 n+1 个元素上的作用都不是可递的. 这也可以从 A_5 作用在它的六个 Sylow 5-子群上看出来. 由此得到了一个略显诡异的群同态 A_5\rightarrow S_6, 从而得到 S_6 的非平凡外自同构, 这也是在所有 S_n 中独一无二的.

(4) 作为旋转变换群, 我们自然有 A_5 的一个三维(不可约)表示.

(5) 上述三维表示实际上是把 A_5 看成 \operatorname{SO}(3) 的子群. 如果注意到群同态 \operatorname{SU}(2)\rightarrow\operatorname{SO}(3) (这来自于四元数), 则有 \operatorname{SU}(2) 的 120 阶子群 A_5^*. 把这个群实现为复矩阵有 9 种本质上不同的方式, 它们之间的关系可以用下图来表示:

此图有几何上的解释: 这里的 9 个点代表 8 维 Euclid 空间中的一组向量, 它们是空间的生成元, 长度相同, 有连线的两个向量的夹角是 120^\circ, 没有连线的向量彼此垂直. 这些向量自然是线性相关的, 组合系数就是图中对应点的标号. 当然, 这些标号有更深刻的内涵——任何一个点的标号恰好等于与它相连的点的标号之和的一半! 能这样标号的图并不多. 诡异的是, 这些图在很多学科中都会出现. (图中的颜色代表什么? 什么也不代表, 好看而已.)

如果去掉标号为 1 的点, 余下 8 个向量是一组基. 有 8 个超平面分别垂直于其中一个基向量, 用这些超平面做反射可以得到 8 个反射变换, 它们生成一个阶数为 2^{14}3^55^27 的有限群 W. 用 W 作用在基向量上一共可以得到 240 个不同向量, 它们在这组基下的坐标都是整数, 并且都是同号的(含零)! 其中坐标和最大的向量是唯一的, 其坐标恰是图中各基向量的标号, 也是标号为 1 的向量的负向量.

这 240 个向量自然具有超强的对称性, 如果把它们投影到一个特殊的二维平面上就得到整个宇宙中最漂亮的图——复单 Lie 代数 E_8 的根系.

(详见数林广记: 《代数学发展史：有限群表示论 I, II》)

群论与 Lie 代数

Lie 代数一般是大四或研究生课程, 不过我认为可以提前以与高等代数、群论更好地结合. 我们很容易注意到 Lie 代数与有限群在概念上的相似性, 可以用下表来展示:

在大学四年级时学到 Lie 代数, 当时就困惑于上面的相似之处. 实际上不仅是名词上的相似, Lie 代数的整个研究思路与前文提到的群论、表示论的研究思路也是完全一致的(我觉得这是代数学的很深的套路). 实际上由于 Lie 代数是线性空间, 其研究要比有限群的研究容易得多, 复单 Lie 单数的分类也简介漂亮的多. 如果了解到 Lie 代数与 Lie 群的关系, 上述相似性就是自然而然的了. 在写群论和 Lie 代数相关文章的时候, 我刻意把二者融合起来: 写一篇群论相关文章, 马上写一篇 Lie 代数相关文章, 以体现这二者的相关性.

(详见:数林广记: 《给大一学生的 Lie 代数》)