关于“1.无定义点=可去间断点？2.振荡、无穷、跳跃、可去间断点究竟啥区别？3.洛必达使用时为啥∫sin（1/x）在x=0可去间断点处能可导？4.函数没有原函数，与函数有定积分是否矛盾？”一点浅见

我为什么写这篇文章，ps：可能主要目的是给自己看的吧，学习数学最大的障碍就类似于标题一样，把基础=简单，实则不然

废话不多说，献给所有跟我一样有同样困惑，年轻的朋友们。

我们先来聊聊无定义点=可去间断点？

我们知道间断点有四类，分别是：可去间断点、跳跃间断点、无穷间断点、振荡间断点。

我先要告诉你的是：这四类间断点都可以是无定义点！

我知道有同志们一定会说：书上定义写的“函数在 x_{0} 处没有定义，称为可去间断点”，所以无定义点只有可去间断点这一种情况！

但是事实真的如此吗？

我们先来就看看振荡、无穷、可去、跳跃间断点为啥都可以是无定义点，且它们之间的区别究竟是什么吧（以下讨论的间断点都是 x_{0}=0 处）

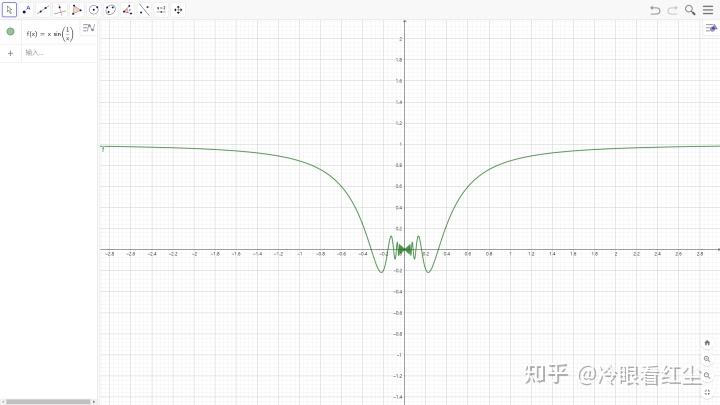
可去间断点例子： f_{(x)}=xcos\left(\frac{1}{x}\right) 或者 f_{(x)}=xsin\left(\frac{1}{x}\right) ，函数如下图所示：

f_{(x)}=xcos\left(\frac{1}{x}\right) 图像如下：

f_{(x)}=xsin\left(\frac{1}{x}\right) 图像如下：

跳跃间断点例子： f_{(x)}=\frac{\left| x \right|}{x} ，函数图像请看下图：

紫色代表函数f_{(x)}=\frac{\left| x \right|}{x} 在x=0处是跳跃间断点！（反正我色弱就这么着吧，我也看不出来啥损色）但是重点来了，x=0处无定义！

无穷间断点： f_{(x)}=\frac{1}{x}cos\left(x\right) 和振荡间断点的情况，请看下图。

蓝色代表函数 f_{(x)}=cos\left(\frac{1}{x}\right) 在x=0处是振荡间断点！并且重点来了，x=0处无定义！

红色代表函数 f_{(x)}=\frac{1}{x}cos\left(x\right) 在x=0处是无穷间断点！并且重点来了，x=0处无定义！

再来个图，考研贼喜欢考：

绿色代表函数是 f_{(x)}=\frac{1}{x}cos\left(\frac{1}{x}\right) 在x=0处是振荡间断点，并且x=0处无定义！这还不是这个函数的关键特殊性，最关键的是它不仅振荡，而且振荡的时候还趋于无穷大！是不是乍一看以为是无穷间断点，有那么点无穷大逼近的味道？可惜它不够“专一”，一会儿无穷大一会儿又趋于0！你问我为啥趋于0，因为 cos\left(\frac{1}{x}\right) 在x→0时，函数可以取到0这个值（这块无数人判断不清楚是无穷间断点和振荡间断点，包括我自己），函数可以取到0这个值的理由如下： \left( 1 \right)当x=\frac{1}{kπ+\frac{π}{2}}且k\rightarrow\infty时\Rightarrow x\rightarrow\ 0， \left( 2 \right)\frac{1}{x}=kπ+\frac{π}{2}，而cos\left( kπ+\frac{π}{2} \right)=0\ \Rightarrow \frac{1}{x}cos\left( \frac{1}{x} \right)=(kπ+\frac{π}{2})\times cos\left( kπ+\frac{π}{2} \right)=0 根据\left( 1 \right)+\left( 2 \right)\Rightarrow\lim_{x \rightarrow \ \frac{1}{kπ+\frac{π}{2} }\Leftrightarrow x\rightarrow0}{\ \frac{1}{x}cos\left( \frac{1}{x} \right)}=0

f_{(x)}=\frac{1}{x}cos\left(\frac{1}{x}\right)，\lim_{x \rightarrow 0}{\frac{1}{x}cos\left(\frac{1}{x}\right)}=不存在，理由如下：

由上可知： \lim_{x \rightarrow \ \frac{1}{kπ+\frac{π}{2} }\Leftrightarrow x\rightarrow0}{\ \frac{1}{x}cos\left( \frac{1}{x} \right)}=0\cdot\cdot\cdot\cdot\cdot\cdot\cdot 极限（1）

\lim_{x \rightarrow \ \frac{1}{kπ}\Leftrightarrow x\rightarrow0}{\ cos\left( \frac{1}{x} \right)}=cos\left( kπ \right)=±1，而\frac{1}{x}=kπ且k\rightarrow\infty\Rightarrow

\lim_{x \rightarrow \ \frac{1}{kπ}\Leftrightarrow x\rightarrow0}{\ \frac{1}{x}cos\left( \frac{1}{x} \right)}=kπ\times cos\left( kπ \right)=±kπ\rightarrow\pm\infty\cdot\cdot 极限（2）

极限（1）=0 ＆极限（2）=±∞故不存在

f_{(x)}=\frac{1}{x}cos\left(\frac{1}{x}\right)图像如下：

再来个大头贴照：

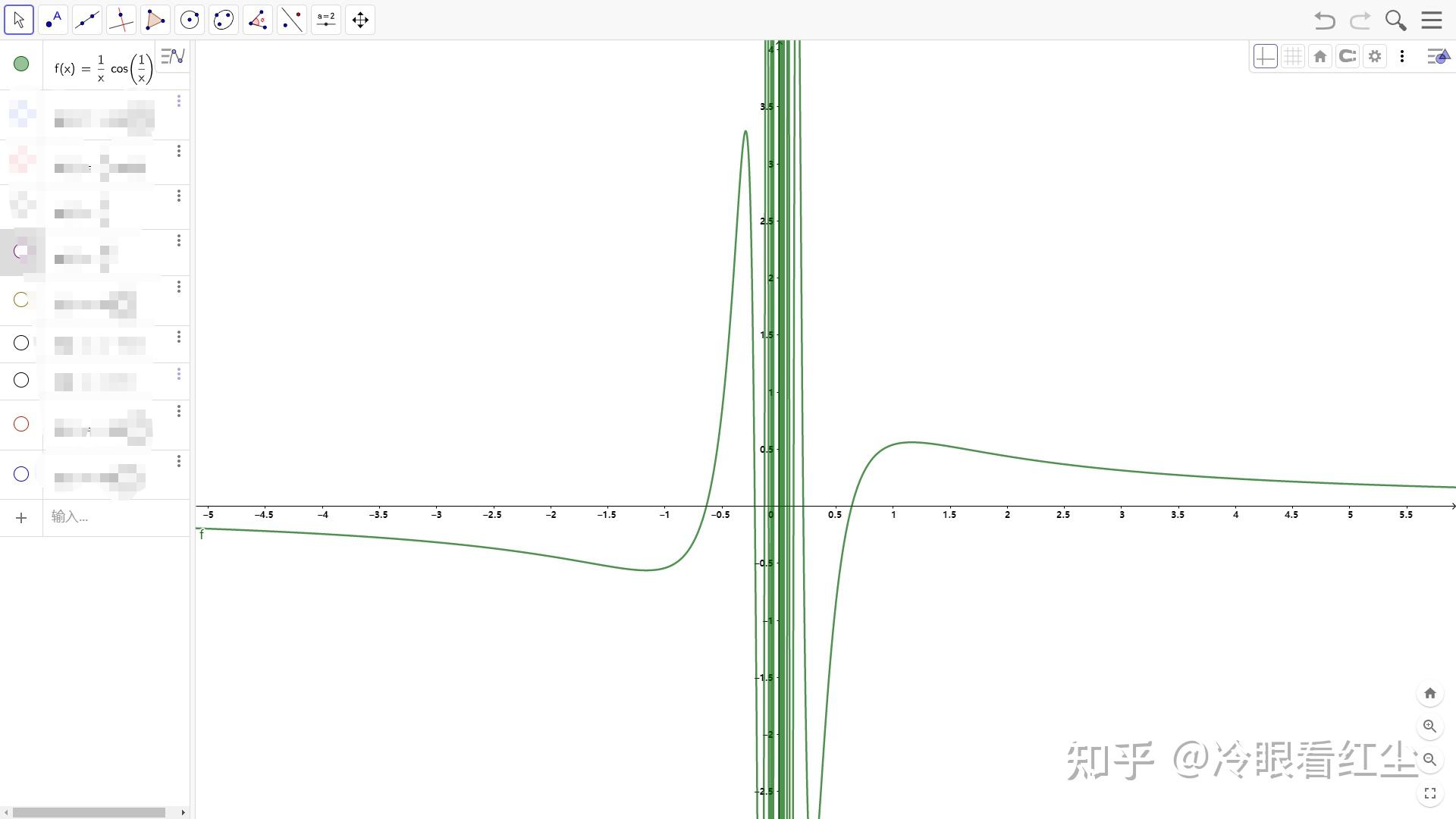
f_{(x)}=\frac{1}{x}cos\left(\frac{1}{x}\right) 在x=0的振荡间断点，这种图像在该点邻域范围内就像个不专一的“海王”不停的振荡，并且在走势过程中函数值接近 \pm\infty ，数学家们给这种类型的振荡图形起了个专门的名字叫“无界振荡”

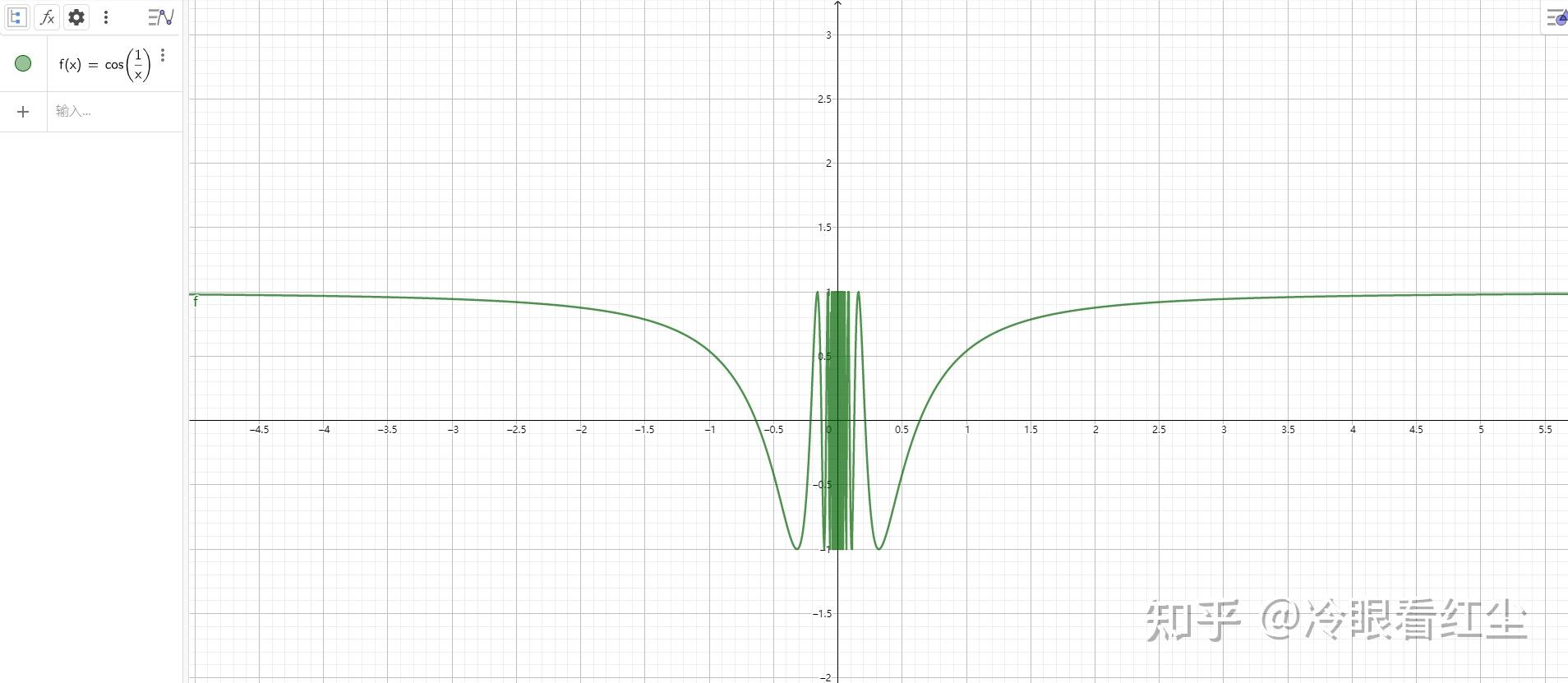
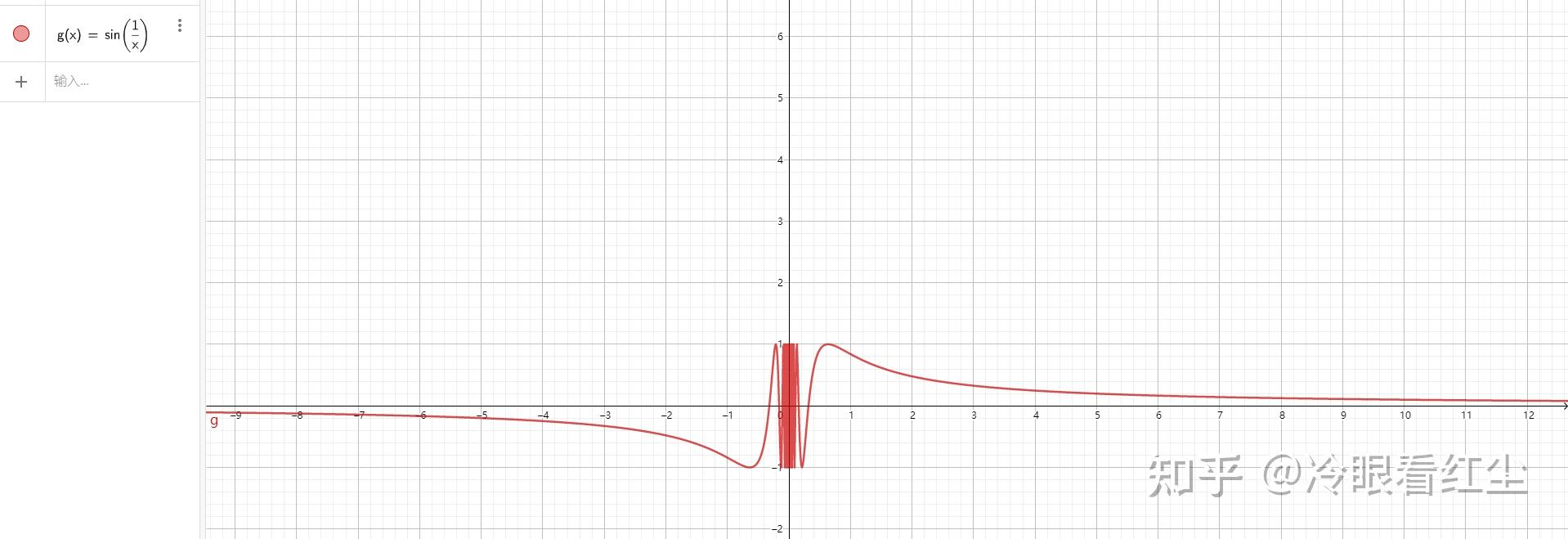
而 f_{(x)}=cos\left(\frac{1}{x}\right)（绿色图像）和 f_{(x)}=sin\left(\frac{1}{x}\right) （红色图像）在x=0处同样也是振荡间断点，但是，函数是有界的，数学家们给这种类型的振荡图形起了个专门的名字叫“有界振荡”

那么我们来看看无穷间断点长什么样子，到底具有什么样的品质？

下图是两个具有无穷间断点的函数图像：

红色函数 f_{(x)}=\frac{1}{x}cos\left(x\right) 和黑色函数 f_{(x)}=\frac{1}{x} （在x=0处是无穷间断点）

再拿下图的跳跃间断点函数f_{(x)}=\frac{\left| x \right|}{x}对比一下，发现啥了没有？

是不是发现跳跃和无穷间断点的函数在单侧去心邻域范围内函数的走势都很“专一”！

好了，我想区别应该大概有个印象了（先回答第二个问题，此处我也跳跃了）。

所以同志们，你们现在还会说无定义点一定都是可去间断点么？

我想答案应该有了吧：

无定义点≠可去间断点，无定义点四种情况均可雨露均沾！

至于这四个点的区别应该也清楚了吧，千万别再说无定义点就一定是可去间断点了！

接下来再聊这个话题“为啥 F_{(x)}=\int_{0}^{x}sin\left( \frac{1}{x} \right)d_{x} F_{(x)} 在x=0是可去间断点，原函数都不存在，为啥还能求导呢？”

同志们，你们现在学了上面以后还会说F_{(x)}在x=0处是可去间断点么？

肯定不会！因为聪明如你，早就发现它是振荡间断点，是可以存在原函数的，也就是说不违背原函数存在定理（达布定理）！当然可以求导！

这个问题主要是因为使用洛必达法则时出现的问题，不过请注意，即使可以求导，但是F_{(x)}在x=0求导以后极限不存在，依然不能使用洛必达！因为 sin\left( \frac{1}{x} \right) 在x=0处是振荡函数，极限不存在

给f_{(x)}=sin\left( \frac{1}{x} \right)再来个放大的自拍头像：

最后再来个经常逛知乎发现的问题：

“函数没有原函数，与函数有定积分是否矛盾？”

还是上图，还是我刚画的那个紫色的函数f_{(x)}=\frac{\left| x \right|}{x} 在x=0处是跳跃间断点，按照原函数存在定理，​函数在x=0这个点没有原函数！但是它求定积分却可积！下图就是\int_{-1.5}^{1.5}\frac{\left| x \right|}{x}d_{x} 可积的示例

所以总结：

“函数没有原函数” 和 “函数有定积分”在一般的条件下并无联系！硬要说联系的话：

那就是在这两种情况下：

①函数存在有限个第一类间断点；或者 ②函数有界且存在有限个振荡间断点（再次强调此处振荡间断点一定得是有界振荡类型，绝对不能是前面提到的无穷振荡！） \Leftrightarrow 函数一定有定积分！

好了，以上如果对你有帮助，请给个赞，让我骄傲一下吧！

以上，如有不对之处，也请各位学术界大佬们轻喷，我会修改文章内容，还请下口之前，原谅本人的水平有限吧！

特别更正一下：

函数 f_{(x)}=xcos\left( x \right) 或者 f_{(x)}=xsin\left( x \right) 在x=0处是连续的！这俩函数没有间断点！没有间断点！没有间断点！（连续写错两次了，真的菜，见谅！）

附上 f_{(x)}=xcos\left( x \right) 的图像：

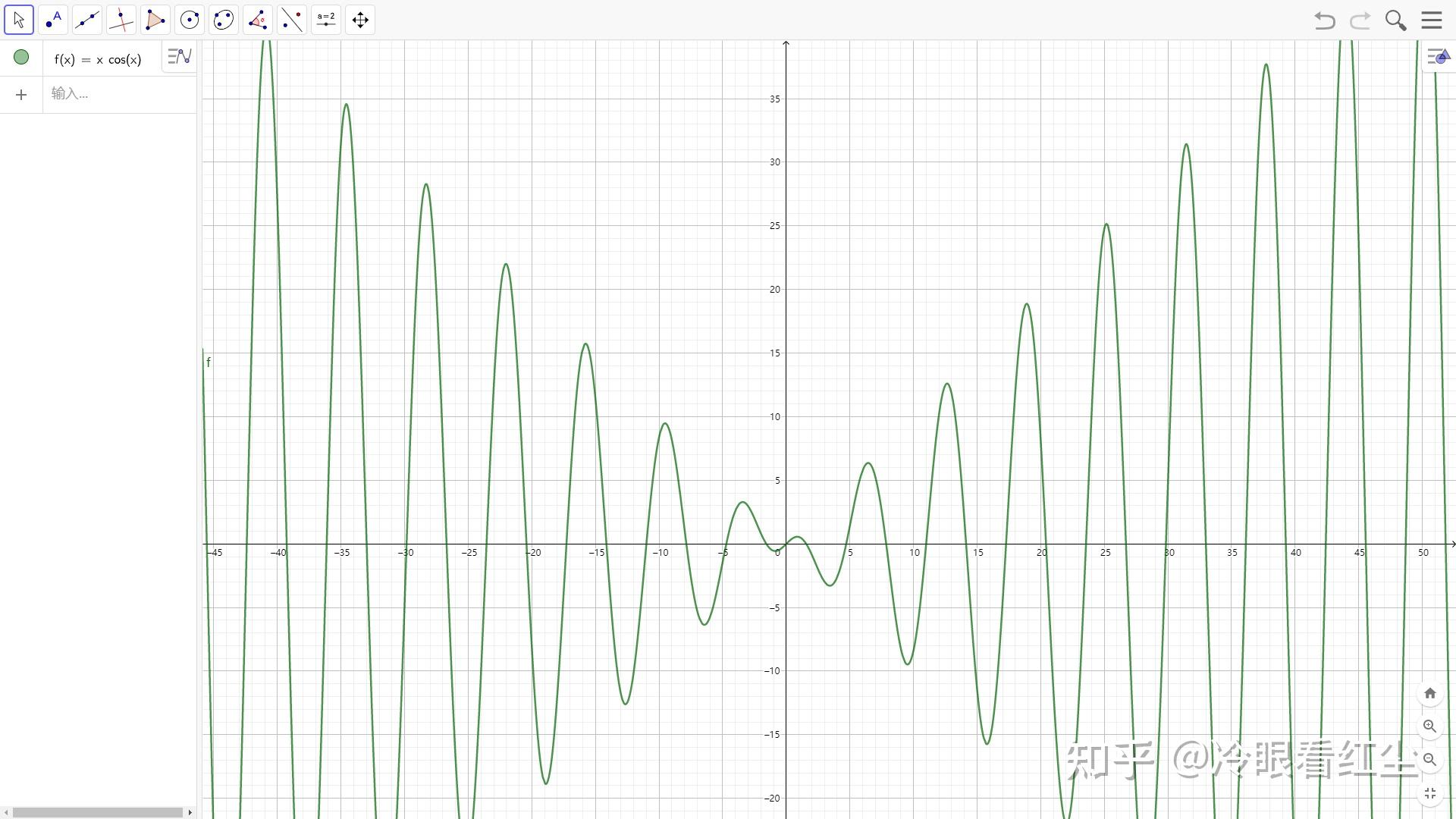
附上f_{(x)}=xsin\left( x \right) 的图像：

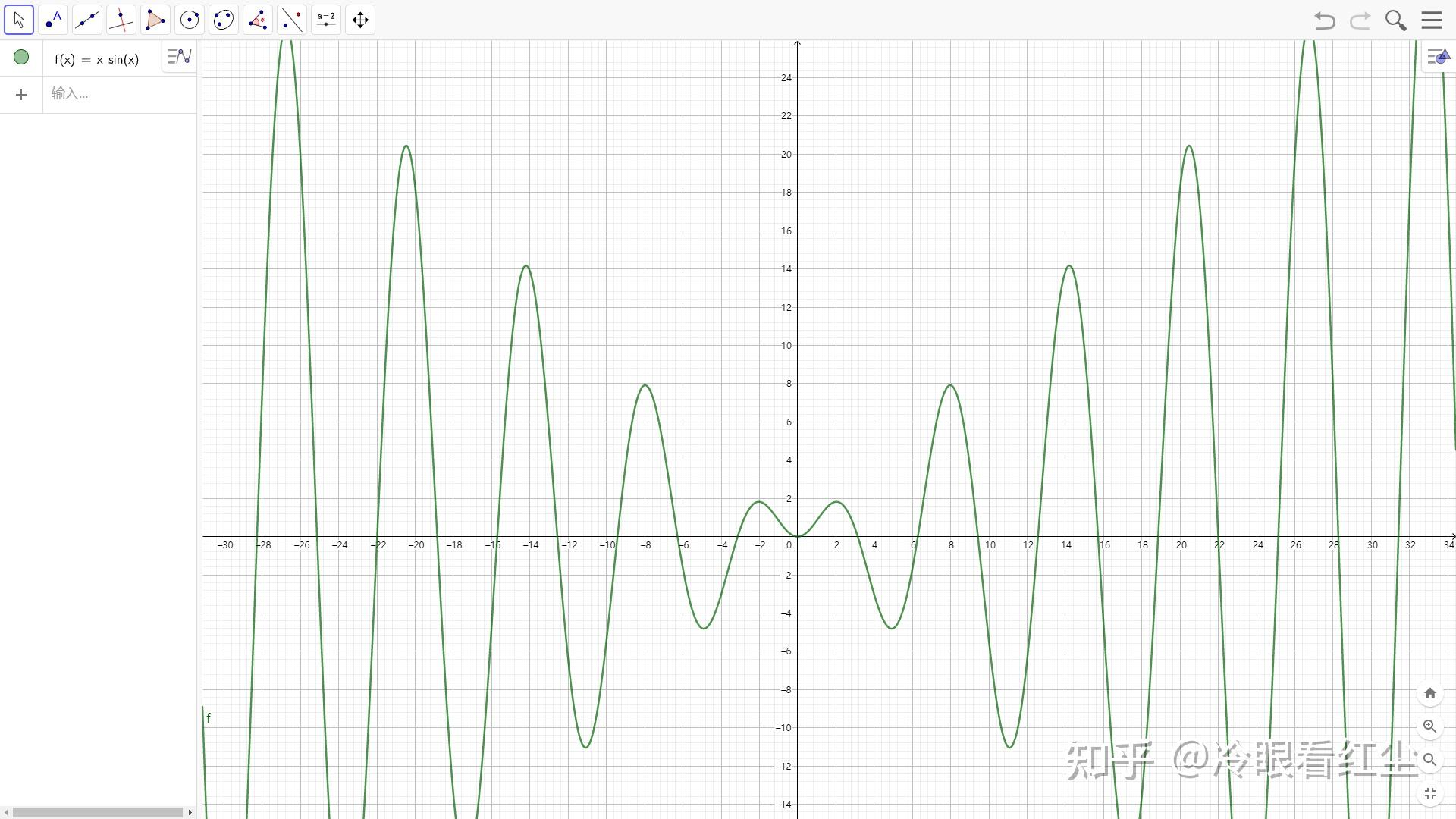
到此为止，我已经把常见和常考的四类复合三角函数的间断情况都做了说明，分别是 f_{(x)}=xcos\left( x \right)； f_{(x)}=xcos\left(\frac{1}{x}\right)； f_{(x)}=\frac{1}{x}cos\left(x\right)； f_{(x)}=\frac{1}{x}cos\left(\frac{1}{x}\right)

特别强调一下函数 f_{(x)}=xsin\left(\frac{1}{x}\right)：

请注意对于这个函数在 x\rightarrow\infty时的极限和x\rightarrow0的极限 ，分别为：

\lim_{x \rightarrow 0}{xsin\left(\frac{1}{x}\right)}=0 ＆ \lim_{x \rightarrow \infty}{xsin\left(\frac{1}{x}\right)}=1

唯独 f_{(x)}=xsin\left(\frac{1}{x}\right) 此函数在 x\rightarrow\infty时和x\rightarrow0时极限都存在，

其他几种组合的函数在两者趋向之间只能有一个存在极限，而另外一个必然不存在极限