平面几何定理之六(三角形角平分线定理)
平面几何定理之六(三角形角平分线定理)
这是平面几何的古老定理,是平面几何最基本的定理之一,但也是最先从初中平面几何删除的内容之一。
定理1 三角形内角平分线分对边成两线段,两线段之比等于相应邻边的比。
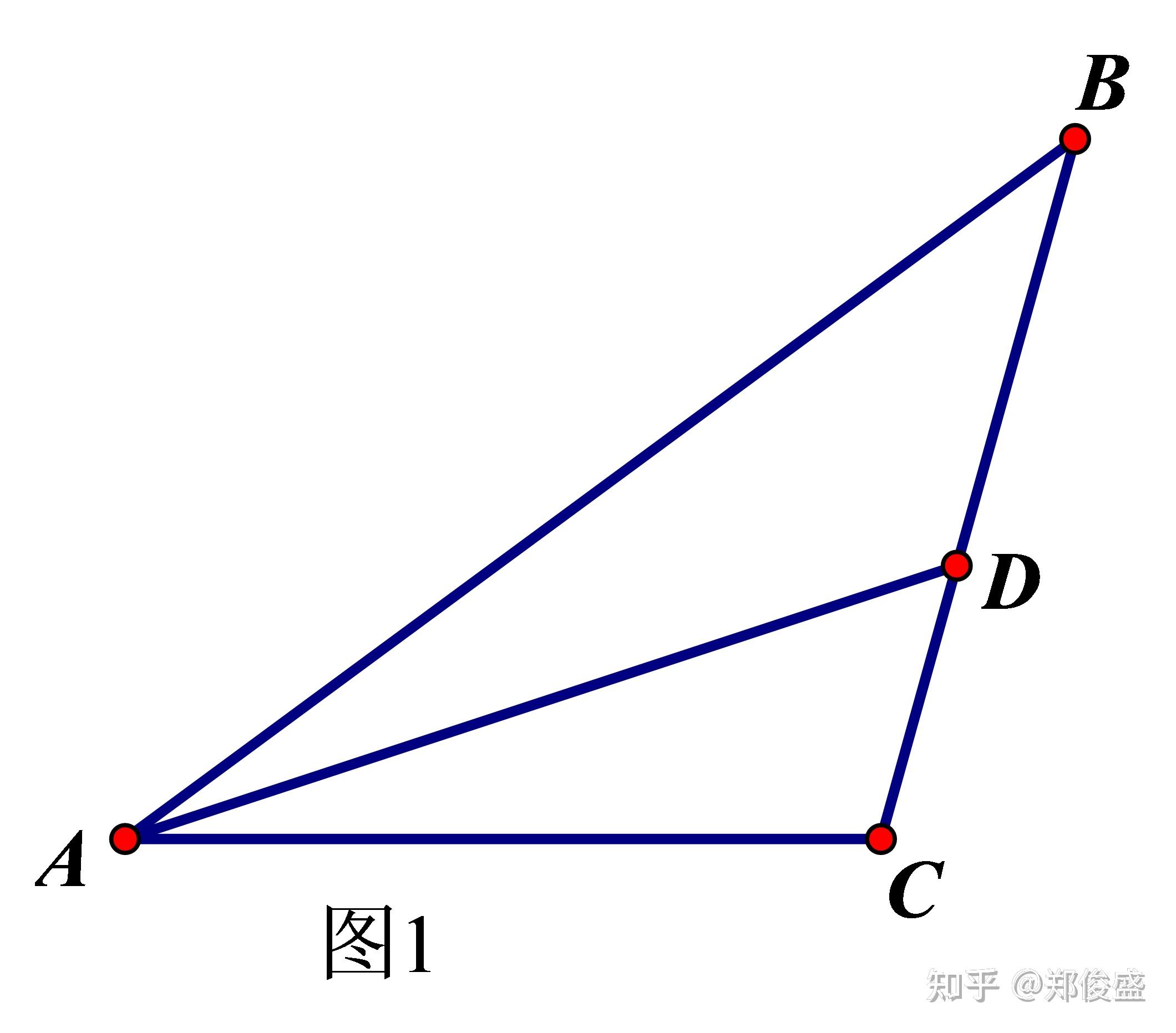
如图1,AD是ΔABC的∠A的平分线,则
\frac{AB}{AC}=\frac{BD}{CD}
分析:如图2,AD是ΔABC的∠A的平分线,则∠BAD=∠CAD,作CE∥DA交BA的延长线于点E,则BA:AE=BD:DC;
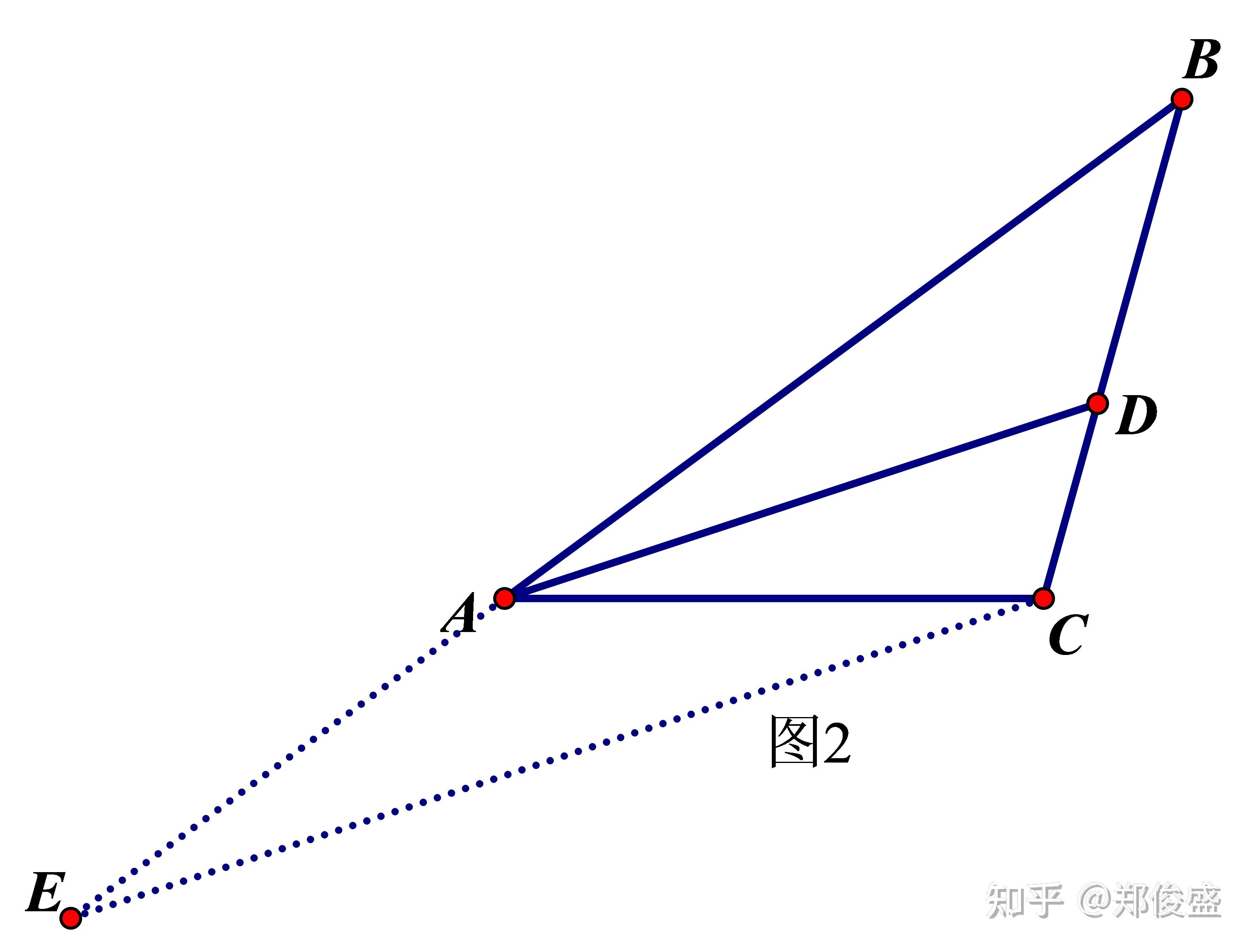
而因为CE∥DA,所以∠CAD=∠ECA,∠BAD=∠E,又∠BAD=∠CAD,所以∠ECA=∠E,所以AC=AE,所以
\frac{AB}{AC}=\frac{BD}{CD}
反之,如上作辅助线,则由于
\frac{AB}{AC}=\frac{BD}{CD},\frac{AB}{AE}=\frac{BD}{CD}
所以
\frac{AB}{AC}=\frac{AB}{AE}
所以AC=AE,从而∠ECA=∠E,又∠BAD=∠E,所以∠BAD=∠CAD,也即是说AD是ΔABC的∠A的平分线。
就是说,定理1的逆定理也是成立的。
定理2 若三角形两边不相等,则其相应外角的平分线外分对边的两线段与相应邻边成比例。
如图3,ΔABC中,AB≠AC,AD是外角∠CAE的平分线,外分边BC成线段BD和CD,则
\frac{AB}{AC}=\frac{BD}{CD}

分析:如图4,AD是ΔABC的∠CAE的平分线,则∠CAD=∠EAD,作CF∥DA交AB于点F,则BF:BA=BC:BD,即1-AF:AB=1-CD:BD,所以AB:AF=BD:CD;

而因为CF∥DA,所以∠CAD=∠ACF,∠DAE=∠AFC,又∠CAD=∠EAD,所以∠AVF=∠AFC,所以AC=AF,所以
\frac{AB}{AC}=\frac{BD}{CD}
由于上述分析都是可逆的,因此同样可以证明,定理2的逆定理也是成立的,具体分析此处略去。
下面举例说明定理的应用。
例1 (高考北京卷理科2003•15)在ΔABC中, a=3,b=2\sqrt{6} ,∠B=2∠A.
(1)求cosA的值;
(2)求 c 的值.
分析:我们画个图,如图5,其中BD是∠ABC的平分线,由于∠B=2∠A,所以∠A=∠CBD,所以ΔABC∽ΔADC,所以CD:BC=BC:AC,所以 CD=\frac{a^{2}}{b}

又因为BD是∠ABC的平分线,所以
\frac{BA}{BC}=\frac{AD}{CD}\Rightarrow\frac{BA+BC}{AC}=\frac{BD+CD}{CD}
即
\frac{a+c}{a}=\frac{b}{CD}\Rightarrow CD=\frac{ab}{a+c}
所以
\frac{ab}{a+c}=\frac{a^{2}}{b}\Rightarrow b^{2}=a^{2}+ac
因为 a=3,b=2\sqrt{6} ,所以
(2\sqrt{6})^{2}=3^{2}+3c\Rightarrow c=5
由余弦定理,得
cosA=\frac{b^{2}+c^{2}-a^{2}}{2bc}=\frac{a+c}{2b}=\frac{8}{4\sqrt{6}}=\frac{\sqrt{6}}{3}
例2 已知ΔABC三边长分别为 a,b,c ,求ΔABC角平分线的长。
分析:分别记∠A,∠B,∠C的角平分线的长为 t_{a},t_{b},t_{c} .
我们以 t_{b} 为例进行分析。

如图6,因为BD是∠ABC的平分线,所以
\frac{BA}{BC}=\frac{AD}{CD}\Rightarrow\frac{BA+BC}{AC}=\frac{BD+CD}{CD}
即
\frac{a+c}{a}=\frac{b}{CD}\Rightarrow CD=\frac{ab}{a+c}
因此
AD=b-\frac{ab}{a+c}=\frac{bc}{a+c}
应用余弦定理,得
cos \angle CBD==\frac{a^{2}+t_{b}^{2}-(\frac{ab}{a+c})^{2}}{2at_{b}}
cos \angleABD=\frac{c^{2}+t_{b}^{2}-(\frac{bc}{a+c})^{2}}{2ct_{b}}
因为∠CBD=∠ABD,所以
\frac{a^{2}+t_{b}^{2}-(\frac{ab}{a+c})^{2}}{2at_{b}}=\frac{c^{2}+t_{b}^{2}-(\frac{bc}{a+c})^{2}}{2ct_{b}}
即
c[a^{2}+t_{b}^{2}-(\frac{ab}{a+c})^{2}]=a[c^{2}+t_{b}^{2}-(\frac{bc}{a+c})^{2}]
化简,得
(a-c)t_{b}^{2}=\frac{(a-c)ac[(a+c+b)(a+c-b)]}{(a+c)^{2}}
令 s=\frac{a+b+c}{2} ,则当 a\nec 时,有
t_{b}^{2}=\frac{4acs(s-b)}{(a+c)^{2}}\Rightarrow t_{b}=\frac{2}{a+c}\sqrt{acs(s-b)}
当 a=c 时,ΔABC是等腰三角形,一方面,由勾股定理,得
t_{b}=\sqrt{a^{2}-(\frac{b}{2})^{2}}
另一方面,由 得,
t_{b}=\frac{2}{2a}\sqrt{a^{2}(2a+b)(2a-b)}=\sqrt{a^{2}-(\frac{b}{2})^{2}}
即,对任意三角形,都有
t_{b}=\frac{2}{a+c}\sqrt{acs(s-b)}
用同样的方法,可得
t_{a}=\frac{2}{b+c}\sqrt{bcs(s-a)},t_{c}=\frac{2}{a+b}\sqrt{abs(s-c)}
例3 (斯库顿(Schooten)定理)任意三角形的角平分线的平方,等于夹这个角的两边的乘积,减去第三边上截得两线段的乘积。
如图7,在ΔABC中,AD是角平分线,定理的意思是
AD^{2}=AB\cdot AC-BD\cdot CD

分析:首先,我们有
\frac{AB}{AC}=\frac{BD}{CD}\Rightarrow AB=\frac{BD}{CD}\cdot AC
其次,过D作∠ADE=∠B,交AC于点E,则因为∠DAE=∠BAD,∠ADE=∠B,所以ΔADE∽ΔABD,所以AB:AD=AD:AE,所以
AD^{2}=AB\cdot AE=AB(AC-CE)=AB\cdot AC-AB\cdot CE
因为∠DEC=∠DAE+∠ADE=∠BAD+∠B=∠ADC,而∠C=∠C,所以ΔADC∽ΔDCE,所以CE:CD=CD:AC,得
CD=\frac{CD^{2}}{AC}
所以
AB\cdot CE=\frac{BD}{CD}\cdot AC\cdot \frac{CD^{2}}{AC}=BD\cdot CD
所以AD^{2}=AB\cdotAC-BD\cdotCD

