【数学分析笔记】9.4 任意项级数

LordBao

抱朴守拙，实事求是

9.4.0 前言

上一节：9.3 正项级数

下一节：10.1 函数项级数的一致收敛性

数学分析笔记整理在：数学分析笔记目录

本节阐述任意项级数。

9.4.1 正文

9.4.1.1 任意项级数

如果仅是有限项为正或负，那么完全可以用正项级数的判别法，故而这里仅研究级数有无限个正项，无限个负项的情况。

柯西收敛原理

补充：若\displaystyle{\sum_{n=1}^\infty}|x_n|级数收敛，则\displaystyle{\sum_{n=1}^\infty}x_n级数收敛。

证明：根据科学收敛原理易得，\forall \varepsilon>0,\exists N>0,\forall n>N与一切的正整数P有：

|x_{n+1}+\dots x_{n+p}| \le |x_{n+1}|+\dots |x_{n+p}| \le ||x_{n+1}|+\dots |x_{n+p}|| < \varepsilon \\

9.4.1.2 Leibniz级数

交错级数和莱布尼兹级数

1处：像负正负正这样下去的级数，其实仅仅与交错级数只是一个符号的差异。

莱布尼兹级数必然收敛

1处：上面的(-1)^{p+1}是怎么来的，观察下标即可。

1处：观察莱布尼兹级数的证明过程即可。

2处：这里|r_n|的绝对值应该可以拿掉，因为r_n是个非负值。

其实1和2都可以统称莱布尼兹级数下，有\displaystyle{\sum_{N}^{N+p}}(-1)^{k+1}u_k \le u_N。

e,g1

e.g2

像这种三角类型的级数，我觉得蛮难的，因为需要一定的观察力。

首先n \pi <\sqrt{n^2+1} \pi <(n+1) \pi,稍微熟悉三角函数的图形，就可以知道该级数是一个交错级数。

然后经过观察就得知\sin (\sqrt{n^2+1} )\pi = (-1)^n\sin (\sqrt{n^2+1}-n) \pi。

9.4.1.3 Abel 判别法和 Dirichlet判别法

这个证明不难，下面是Abel变换的直观理解：

Abel引理

阿贝尔判别法和狄利克雷判别法

但这个条件不一定满足吧。

e.g1

1处：这个应该确实是单调的，但是具体证明我忘了，暂时不管这个细节。

e.g2

积化和差公式(来自百度)

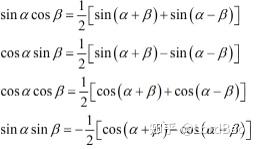
算的时候注意\sin kx \sin \frac{x}{2}这样来算，更加直观，中间项通通都消掉了。

证明是类似的，同样是左边乘以2 \sin \frac{x}{2},然后推出\displaystyle{\sum_{k=1}^n}\cos kx是有界的。当x=2k\pi时，有\cos nx=1,此时级数不一定收敛，考虑\frac{1}{n}和\frac{1}{n^2}的情况。这个连同上面那个例子，当做是一个结论吧。

9.4.1.4 级数的绝对收敛和条件收敛

引言

绝对收敛和条件收敛

e.g1

e.g2

由于 0<x<\pi,故而2x \ne 2k\pi,因此根据例9.4.3可得此时\displaystyle{\sum_{k=1}^n}\cos k2x是有界，则\displaystyle{\sum_{n=1}^{\infty}}a_n \cos n2x收敛。

定理

注意正项级数要么收敛，要么发散于正无穷。因为正项级数不收敛的话，那么它一定没有上界，\forall M>0,\exists N,满足\displaystyle{\sum_{n=1}^N}x_n \ge M,但是由于是正项级数，那么不难得到，\forall M>0,\exists N,当n>N时有\displaystyle{\sum_{k=1}^n}x_k \ge M，故而级数发散于正无穷。

9.4.1.5 加法交换律

引言

e.g1

定理

从证明来看，应该补一个结论\displaystyle{\sum_{n=1}^\infty}|x_n|=\displaystyle{\sum_{n=1}^\infty}|x_n'|。

定理

1处：这个就暂时不证明了。

2处：这个最小的含义是说x_1^++x_2^+\dots+x_{n_1-1}^+ \le a，故而x_1^++x_2^+\dots+x_{n_1-1}^++x_{n_1}^+ \le a + x_{n_1}^+。

9.4.1.6 级数的乘法

引言

级数乘法的对角线排列（柯西乘积）

级数乘法的正方形排列

假设级数\displaystyle{\sum_{n=1}^\infty}a_n和级数\displaystyle{\sum_{n=1}^\infty}b_n的部分和分别为S_n',S_n''，那么级数\displaystyle{\sum_{n=1}^\infty}d_n的部分和为S_n=S_n'S_n'',那么\displaystyle{\sum_{n=1}^\infty}d_n=(\displaystyle{\sum_{n=1}^\infty}a_n)(\displaystyle{\sum_{n=1}^\infty}b_n)。

这里的外部应该是(-1)^{n+3}，但是影响不大。

定理

1处：举个例子吧，比如n=3时，前3个乘积之和可以是a_1b_2+a_2b_3+a_2b_4，那么N=4。此时显然有|a_1b_2|+|a_2b_3|+|a_2b_4| \le \displaystyle{\sum_{i=1}^4|a_i|}\displaystyle{\sum_{j=1}^4|b_j|}。

2处：级数\displaystyle{\sum_{n=1}^\infty}d_n确实可以看做先更序，再加括号。

这个定理有点抽象了，看不懂记结论就行了。

e.g

9.4.2 总结

任意项级数

仅是有限项为正或负，那么完全可以用正项级数的判别法，故而这里仅研究级数有无限个正项，无限个负项的情况。
级数柯西收敛原理。
级数柯西收敛原理推论

级数收敛，则通项趋于0。
若\displaystyle{\sum_{n=1}^\infty}|x_n|级数收敛，则\displaystyle{\sum_{n=1}^\infty}x_n级数收敛。

Leibniz级数

交错级数和莱布尼兹级数的定义。
莱布尼兹级数必然收敛。
莱布尼兹级数下，有\displaystyle{\sum_{N}^{N+p}}(-1)^{k+1}u_k \le u_N。

Abel 判别法和 Dirichlet判别法

Abel变换：假设\{a_n\},\{b_n\}为数列，B_p=\displaystyle{\sum_{i=1}^{p}}b_i，那么\displaystyle{\sum_{i=1}^{p}}a_ib_i=a_pB_p-\displaystyle{\sum_{i=1}^{p-1}}(a_{i+1}-a_{i})B_i。
Abel引理：若\{a_n\}为单调数列，\{b_n\}为数列,\{B_k\}为一数列，其满足B_k=\displaystyle{\sum_{i=1}^{k}}b_i。若存在M>0,对一切的k满足|B_k| \le M,那么有|\displaystyle{\sum_{i=1}^{p}}a_ib_i| \le M(|a_1|+2|a_p|)。
Abel判别法：如果\{a_n\}单调有界，级数\displaystyle{\sum_{i=1}^{\infty}}b_i收敛，那么\displaystyle{\sum_{i=1}^{\infty}}a_ib_i收敛。
Dirichlet判别法：如果\{a_n\}单调且收敛于0，级数\displaystyle{\sum_{i=1}^{\infty}}b_i有界，那么\displaystyle{\sum_{i=1}^{\infty}}a_ib_i收敛。
若数列\{a_n\}单调趋于0，且x不为2k\pi的任意实数，此时\displaystyle{\sum_{k=1}^n}\sin kx是有界，则\displaystyle{\sum_{n=1}^{\infty}}a_n \sin nx收敛。当x为2k \pi时，\displaystyle{\sum_{n=1}^{\infty}}a_n \sin nx收敛于0。
若数列\{a_n\}单调趋于0，且x不为2k\pi的任意实数，此时\displaystyle{\sum_{k=1}^n}\cos kx是有界，则\displaystyle{\sum_{n=1}^{\infty}}a_n \cos nx收敛。当x为2k \pi时，\displaystyle{\sum_{n=1}^{\infty}}a_n \cos nx不一定收敛。

级数的绝对收敛和条件收敛

级数的绝对收敛和条件收敛的定义。
一般而言，若\displaystyle{\sum_{n=1}^\infty}|x_n|级数发散，则\displaystyle{\sum_{n=1}^\infty}x_n级数不一定发散。但是若是由Cauchy判别法或d'Alembert判别法判定出来的\displaystyle{\sum_{n=1}^\infty}|x_n|级数发散，那么\displaystyle{\sum_{n=1}^\infty}x_n级数也发散，因为由Cauchy判别法或d'Alembert判别法判断出发散的话，那么|x_n|不趋于0，那么x_n也不趋于0，显然即不满足级数收敛的必要条件。
考虑级数\displaystyle{\sum_{n=1}^\infty}x_n，令x_n^+=\frac{|x_n|+|x_n|}{2},x_n^-=\frac{|x_n|-|x_n|}{2},那么\displaystyle{\sum_{n=1}^\infty}x_n^+代表级数\displaystyle{\sum_{n=1}^\infty}x_n的所有正项构成的级数，\displaystyle{\sum_{n=1}^\infty}x_n^-代表级数\displaystyle{\sum_{n=1}^\infty}x_n的所有负项取反得到的级数。且当\displaystyle{\sum_{n=1}^\infty}x_n绝对收敛时，\displaystyle{\sum_{n=1}^\infty}x_n^+和\displaystyle{\sum_{n=1}^\infty}x_n^-都收敛；当\displaystyle{\sum_{n=1}^\infty}x_n条件收敛时，\displaystyle{\sum_{n=1}^\infty}x_n^+和\displaystyle{\sum_{n=1}^\infty}x_n^-发散于正无穷。

级数的加法交换律

数项级数不一定满足交换律。
级数\displaystyle{\sum_{n=1}^\infty}x_n绝对收敛，则其更序级数\displaystyle{\sum_{n=1}^\infty}x_n'也绝对收敛，且\displaystyle{\sum_{n=1}^\infty}x_n=\displaystyle{\sum_{n=1}^\infty}x_n'及\displaystyle{\sum_{n=1}^\infty}|x_n|=\displaystyle{\sum_{n=1}^\infty}|x_n'|。此时说明在一定条件下，数项级数满足交换律。
级数\displaystyle{\sum_{n=1}^\infty}x_n条件收敛，则对于任意的-\infty\le a \le +\infty(包括正无穷和负无穷)，均能找到级数\displaystyle{\sum_{n=1}^\infty}x_n的更序级数\displaystyle{\sum_{n=1}^\infty}x_n'，使得其收敛于a。

级数的乘法

级数乘法的对角线排列（柯西乘积）
级数乘法的正方形排列。假设级数\displaystyle{\sum_{n=1}^\infty}a_n和级数\displaystyle{\sum_{n=1}^\infty}b_n均收敛，那么级数乘法的正方形排列\displaystyle{\sum_{n=1}^\infty}d_n必然收敛，且\displaystyle{\sum_{n=1}^\infty}d_n=(\displaystyle{\sum_{n=1}^\infty}a_n)(\displaystyle{\sum_{n=1}^\infty}b_n)。
假设级数\displaystyle{\sum_{n=1}^\infty}a_n和级数\displaystyle{\sum_{n=1}^\infty}b_n均收敛，那么柯西乘积\displaystyle{\sum_{n=1}^\infty}c_n不一定收敛。
假设级数\displaystyle{\sum_{n=1}^\infty}a_n和级数\displaystyle{\sum_{n=1}^\infty}b_n均绝对收敛，那么将a_ib_j以任意形式排列的级数也必然绝对收敛，且级数收敛于(\displaystyle{\sum_{n=1}^\infty}a_n)(\displaystyle{\sum_{n=1}^\infty}b_n)。