I have previously written about Spinoza’s rejection of a standard theological argument against his belief that God produces everything it is in his power to produce. The argument, roughly, is that if God produces everything it is in his power to produce, then there must be some limit on his power. Supposing that God produces a race of giants to the extent of his power, take the tallest giant in the race; it must be that God could not have produced a taller one.
The argument seems to involve an implicit rejection of infinite domains — otherwise we could say that in such a case there is no tallest giant produced by God, just as there is no largest prime number. But to think of such a case involves reference to an actual rather than merely potential infinity, and as Poincaré pointed out (before criticising the ideas of Russell and Cantor), such an idea was traditionally alien to mathematical theory:
The notion of infinity had long since been introduced into mathematics, but this infinity was what philosophers call a becoming. Mathematical infinity was only a quantity susceptible of growing beyond all limit; it was a variable quantity of which it could not be said that it had passed, but only that it would pass, all limits.
In this case we could say, of some group of giants, that there exists outside that group some taller giant, but we cannot speak of the group of all the giants and say that for any one in that group there is another, taller giant in the same group. For that group would then have to be an actual infinity — a quantity that ‘has passed all limits’ — for reasons Poincaré explained in detail with reference to paradoxes of non-predicative definitions.
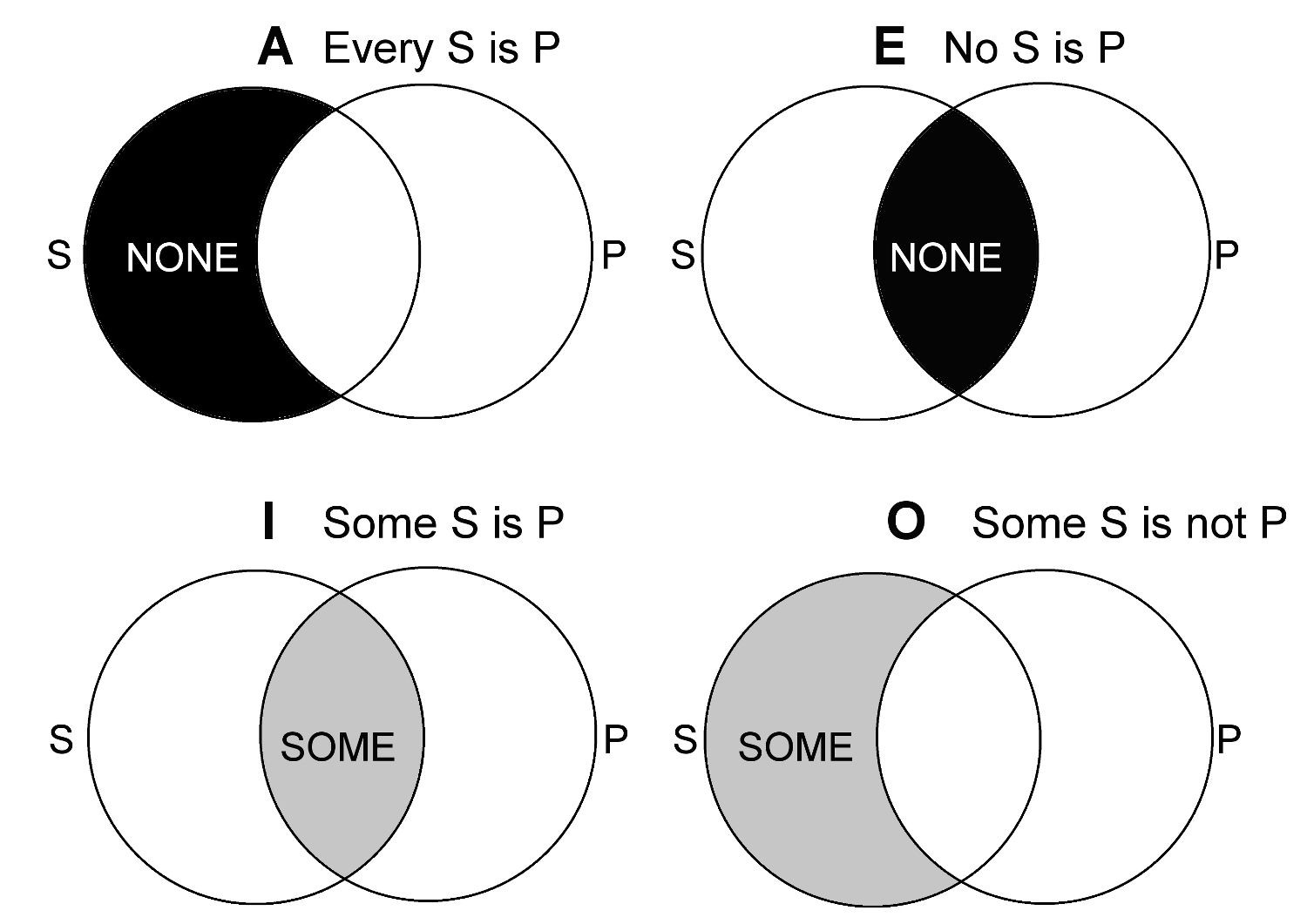
Within the traditional theory of inference — the syllogistic — there is a more interesting restriction on generality. All syllogistic terms must have instances (this is to preserve the traditional Square of Opposition, among other things). Without negative terms there is no way to speak with absolute generality; we can say that all S are P but there is no way to express the thought that everything is P. With negative terms it becomes formally possible to express thoughts about everything. We can have, SaP; S’aP: all S’s are P; all non-S’s are P. By the law of excluded middle, everything must be P. But this formal possibility is ruled out if all terms have instances. For if P is a term then so is P’. But, as Neville Keynes showed, ordinary rules of conversion can allow us to draw inferences from SaP; S’aP that are contradictory unless P’ is taken as empty:
SaP = SeP’ = P’eS
S’aP = S’eP’ = P’eS’ = P’aS
If both all and no P’ are S then there must be no P’, but then P’ is an empty term.
The upshot is that syllogistic provides no way to speak of everything — not even within a domain. For if S and P are non-empty terms within any domain comprising a model for inferences — what Lewis Carroll called the ‘universe of discourse’ — then S’ and P’, if they are to be accepted as terms, must also be non-empty within that domain; after all they can combined with the other terms and each other according to the various quantities and qualities. Absolute generality is implicitly rejected in the syllogistic, so long as we respect the existential import of all terms. The universe of discourse must be inexhaustible by the terms of our discourse.
A.N. Prior (Formal Logic, second edition, 129–30) complains that if we take seriously the stricture forbidding non-empty terms then we can also generate the result that SeP and S’eP’ will never be jointly false. Yet, he notes, if we take ‘man’ for S and ‘non-man’ for P we seem to have a clear countermodel to this rule: no men are non-men, but no non-men are non-non-men (i.e. men). This countermodel is, however, perhaps already implicitly rejected by the inexhaustibility condition on the universe of discourse, since men and non-men together seem to exhaust the domain of things under discussion. If we form a term, M, such that SaM and S’aM, then M will be a term for everything altogether, whether a man or not, and M’ will then be empty.
It follows from this inexhaustibility condition that, within the constraints of the syllogistic, we can’t reason about what is in God’s power. To do so, we would have to take what is in God’s power as a term. And then its negative, given divine omnipotence, will be empty.
How then could theologians reason about divine omnipotence? I suppose it is the kind of thing that can be shown but not said. For any group of things we conceive or speak of as being in God’s power, there will be other things we are not conceiving or speaking of that are also in God’s power — God’s power is then the ‘universe of discourse’, which, like all such universes within syllogistic, is inexhaustible by our powers of expression, no matter how far we extend them.
Spinoza, following Descartes (or so I argue), probably rejected the syllogistic as a complete model of inference. But elsewhere he seems to appeal to the rejection of absolute generality — namely in his arguments against the divisibility of infinite extension in the Scholium to Proposition 17 of the Ethics. At least, as I read those arguments, they consist of a denial that infinite extension could be composed of any set of finite regions.
Alison Peterman’s excellent paper on extension in Spinoza puts the point in this way. Spinoza argues that finite bodies can’t compose an infinite extension for the same reason that points can’t compose a line. But, Peterman notes, points can’t compose a line because they are zero-dimensional and lines are one-dimensional. Does it follow that infinite extension is four-dimensional?! Peterman suggests that Spinoza’s analogy aims at a more general result: finite bodies cannot compose infinite extension because they are the wrong sort of thing to compose it.
In the background here, I think, is the sort of sceptical attitude towards actual infinity found in Aristotle’s Metaphysics. But it is difficult to see what grounds that rejection if not some more general rejection of absolute generality: why could we not, e.g., speak of all the finite bodies in a group such that for any finite set of bodies in that group there are others besides? Such a group, provided the bodies didn’t overlap, would compose an infinitely extended body.
Spinoza aimed, of course, to demonstrate his philosophy more geometrico. The problem is that there was no formal theory of inference to explain what governs geometrical reasoning (for that, at least for Euclidean geometry, we have to wait for Schwäbhauser, Szmielew, and Tarski). Certainly the syllogistic won’t work; Descartes showed in the Rules for the Direction of the Mind that it doesn’t cover ordinary arithmetical inferences. But in the absence of such a theory we need to answer questions such as that of the permissibility of absolute generality. In the absence of a theory of inference, it is unsurprising that Spinoza should appear to have not made up his mind about absolute generality.
