文章目录
有界线性算子与算子空间
有界线性算子

分析:
- 算子:就是映射
- 线性算子: T ( α x + β y ) = α T x + β T y T(\alpha x + \beta y) = \alpha T x + \beta T y T(αx+βy)=αTx+βTy
- 存在常数 C > 0 C>0 C>0,对任意 x ∈ X x\in X x∈X,有 ∣ ∣ T x ∣ ∣ ≤ C ∣ ∣ x ∣ ∣ ||Tx||\le C||x|| ∣∣Tx∣∣≤C∣∣x∣∣
定理:有限维赋范空间X上的任一线性算子T都是有界的

上面的证明有一丝说不过去:
- 最后一步 ≤ \le ≤怎么过来的?
- 需要进一步了解,阅读专业泛函资料
算子空间B(X,Y)

值得注意的是:
- 算子空间是
关于算子的集合 -
∣
∣
T
∣
∣
||T||
∣∣T∣∣是
最小上界 s u p sup sup - 这个
最小+上界我们将在下面的例题中感受到
||T||满足范数三条:B(X,Y)关于||T||构成赋泛空间

如上:
- 因为满足三条
- 所以是范数,所以构成赋泛空间
例题:求||T||

如上,两部分:
- 证明 ∣ ∣ T ∣ ∣ ≤ e ||T||\le e ∣∣T∣∣≤e
- 证明 ∣ ∣ T ∣ ∣ ≥ e ||T||\ge e ∣∣T∣∣≥e
- 所以有 ∣ ∣ T ∣ ∣ = e ||T|| = e ∣∣T∣∣=e
思路:
- 线性
T
(
α
x
+
β
y
)
=
α
T
x
+
β
T
y
T(\alpha x + \beta y) = \alpha T x + \beta T y
T(αx+βy)=αTx+βTy -> 有界
∣
∣
T
x
∣
∣
||Tx||
∣∣Tx∣∣与
∣
∣
x
∣
∣
||x||
∣∣x∣∣的关系 ->
T
T
T有界线性
- 其中,要利用 T T T与 ∣ ∣ x ∣ ∣ ||x|| ∣∣x∣∣在本题目中的具体定义(如何算的)
-
x
x
x是一个关于
t
t
t的函数,另
x
1
≡
1
x1\equiv 1
x1≡1(恒等于1)
- 可得此使的 ∣ ∣ T x ∣ ∣ = e ||Tx||=e ∣∣Tx∣∣=e
- 而带入 ∣ ∣ T x ∣ ∣ ∣ ∣ x ∣ ∣ \frac{||Tx||}{||x||} ∣∣x∣∣∣∣Tx∣∣的式子,得到值为 e e e
- 这说明 s u p . . . sup... sup...一定大于等于 e e e,即 ∣ ∣ T ∣ ∣ ≥ e ||T||\ge e ∣∣T∣∣≥e
- 为什么?因为
s
u
p
sup
sup是
最小上界,在 x x x为某一值A时, s u p sup sup为某一值B,则说明 s u p sup sup最小为B,否则就不是所有 x x x对应的最小上界了
例题
例题1:证明线性赋泛空间中成立某一关系
∣ ∣ ∣ x ∣ ∣ − ∣ ∣ y ∣ ∣ ∣ ≤ ∣ ∣ x − y ∣ ∣ |||x||-||y||| \le ||x-y|| ∣∣∣x∣∣−∣∣y∣∣∣≤∣∣x−y∣∣
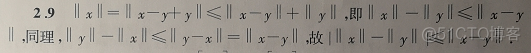
分析:
- 既然要证明绝对值,那就把绝对值打开,正负都证一遍
- 如何才能把构造多个范数的关系?使用性质(3),则有 ∣ ∣ x ∣ ∣ = ∣ ∣ x − y + y ∣ ∣ ≤ ∣ ∣ x − y ∣ ∣ + ∣ ∣ y ∣ ∣ ||x|| = ||x-y+y||\le ||x-y|| + ||y|| ∣∣x∣∣=∣∣x−y+y∣∣≤∣∣x−y∣∣+∣∣y∣∣
例题2:证明是线性算子


分析:
- 是线性算子,则证明 T ( α x + β y ) = α T x + β T y T(\alpha x + \beta y) = \alpha T x + \beta T y T(αx+βy)=αTx+βTy即可
例题3:是子空间

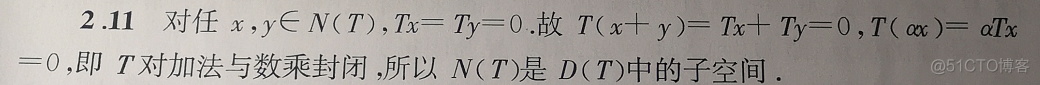
分析:
- 是子空间,即对加法和数乘封闭
例题4:证明线性无关组


分析:
- 如果想证明 A , . . . , Z {A,...,Z} A,...,Z是线性无关组,构造 k 1 A + . . . + k n Z = 0 k_1A+...+k_n Z = 0 k1A+...+knZ=0,证明其中必有 k 1 = . . . = k n = 0 k_1=...=k_n=0 k1=...=kn=0即可
- 利用了 T T T是线性,可以提出来的性质
- 又利用了 T − 1 T^{-1} T−1存在的性质

















