2.4: Harmonic, Subharmonic, and Plurisubharmonic Functions
- Page ID
- 74231
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Let \(U \subset \mathbb{R}^n\) be an open set. A \(C^2\)-smooth function \(f \colon U \to \mathbb{R}\) is harmonic if\(^{1}\) \[\nabla^2 f = \frac{\partial^2 f}{\partial x_1^2} + \cdots + \frac{\partial^2 f}{\partial x_n^2} = 0 \quad \text{ on $U$.}\]
A function \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is subharmonic if it is upper-semicontinuous \(^{2}\) and for every ball \(B_r(a)\) with \(\overline{B_r(a)} \subset U\), and every function \(g\) continuous on \(\overline{B_r(a)}\) and harmonic on \(B_r(a)\), such that \(f(x) \leq g(x)\) for \(x \in \partial B_r(a)\), we have \[f(x) \leq g(x), \quad \text{ for all } x \in B_r(a) .\]
In other words, a subharmonic function is a function that is less than every harmonic function on every ball. We remark that when \(n=1\) in the definition of a subharmonic function, it is the same as the standard definition of a convex function of one real variable, where affine linear functions play the role of harmonic functions: A function of one real variable is convex if for every interval it is less than the affine linear function with the same end points. After all, a function of one real variable is harmonic if the second derivative vanishes, and it is therefore affine linear. In one real dimension it is also easier to picture. The function \(f\) is convex if on every interval \([\alpha,\beta]\), \(f \leq g\) for every affine linear \(g\) bigger than \(f\) at the endpoints \(\alpha\) and \(\beta\). In particular, we can take the \(g\) that is equal to \(f\) at the endpoints. See . The picture is analogous for subharmonic functions for \(n > 1\), but it is harder to draw.
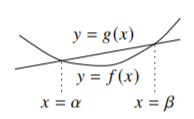
Figure \(\PageIndex{1}\)
We will consider harmonic and subharmonic functions in \(\mathbb{C} \cong \mathbb{R}^2\). Let us go through some basic results on harmonic and subharmonic functions in \(\mathbb{C}\) that you have seen in detail in your one-variable class. Consequently, we leave some of these results as exercises. In this section (and not just here) we often write \(f(z)\) for a function even if it is not holomorphic.
An upper-semicontinuous function achieves a maximum on compact sets.
Let \(U \subset \mathbb{C}\) be open. Show that for a \(C^2\) function \(f \colon U \to \mathbb{R}\),
\[\frac{\partial^2}{\partial \bar{z}\partial z} f = \frac{1}{4} \nabla^2 f . \nonumber\]
Use this to show that \(f\) is harmonic if and only if it is (locally) the real or imaginary part of a holomorphic function. Hint: The key is finding an antiderivative of a holomorphic function.
Prove the identity theorem. Let \(U \subset \mathbb{C}\) be a domain and \(f \colon U \to \mathbb{R}\) harmonic such that \(f=0\) on a nonempty open subset of \(U\). Then \(f\equiv 0\).
It follows from the exercise that a harmonic function is infinitely differentiable. It is useful to find a harmonic function given boundary values. This problem is called the Dirichlet problem, and it is solvable for many (though not all) domains. The proof of the following special case is contained in the exercises following the theorem. The Poisson kernel for the unit disc \(\mathbb{D} \subset \mathbb{C}\) is
\[P_r(\theta) = \frac{1}{2\pi} \frac{1-r^2}{1+r^2-2r \cos \theta} = \frac{1}{2\pi} \operatorname{Re} \left( \frac{1+re^{i\theta}}{1-re^{i\theta}}\right) , \qquad \text{for $0 \leq r < 1$.}\]
Let \(u \colon \partial \mathbb{D} \to \mathbb{R}\) be a continuous function. The function \(Pu \colon \overline{\mathbb{D}} \to \mathbb{R}\), defined by \[Pu(re^{i\theta}) = \int_{-\pi}^\pi u(e^{it}) P_r(\theta-t) \, dt \quad \text{if $r < 1$} \qquad \text{and} \qquad Pu(e^{i\theta}) = u(e^{i\theta}), \] is harmonic in \(\mathbb{D}\) and continuous on \(\overline{\mathbb{D}}\).
In the proof, it is useful to consider how the graph of \(P_r\) as a function of \(\theta\) looks for a fixed \(r\). See Figure \(\PageIndex{2}\).
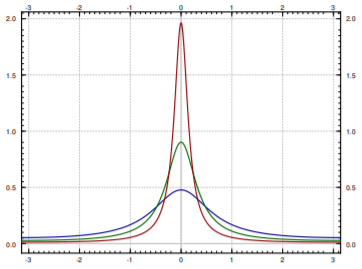
Figure \(\PageIndex{2}\)
- Prove \(P_r(\theta) > 0\) for all \(0 \leq r < 1\) and all \(\theta\).
- Prove \(\int_{-\pi}^{\pi} P_r(\theta) \, d\theta = 1\).
- Prove for any given \(\delta > 0\), \(\sup \{P_r(\theta) : \delta \leq |\theta| \leq \pi \} \to 0\) as \(r \to 1\).
Prove Theorem \(\PageIndex{1}\) using the following guideline:
- Poisson kernel is harmonic as a function of \(z=re^{i\theta} \in \mathbb{D}\), and hence \(Pu\) is harmonic.
- \(P\) acts like an approximate identity: Prove that \(Pu(re^{i\theta}) \to u(e^{i\theta})\) uniformly as \(r \to 1\). Hint: Split the integral to \([-\delta,\delta]\) and the rest and use the previous exercise.
- Prove that \(Pu(z)\) tends to \(u(z_0)\) as \(z \in \mathbb{D} \to z_0 \in \partial \mathbb{D}\).
State and prove a version of Theorem \(\PageIndex{1}\) for an arbitrary disc \(\Delta_r(a)\).
Prove that the Dirichlet problem is not solvable in the punctured disc \(\mathbb{D} \setminus \{ 0 \}\). Hint: Let \(u = 0\) on \(\partial \mathbb{D}\) and \(u(0)=1\). The solution would be less than \(- \epsilon \log |z|\) for every \(\epsilon > 0\).
The Poisson kernel is a reproducing kernel for holomorphic functions, as (the real and imaginary parts of) holomorphic functions are harmonic. Poisson kernel exists for higher dimensions as well. Solving the Dirichlet problem using the Poisson kernel leads to the following result.
Let \(U \subset \mathbb{C}\) be an open set.
- A continuous function \(f \colon U \to \mathbb{R}\) is harmonic if and only if \[f(a) = \frac{1}{2\pi} \int_0^{2\pi} f(a+re^{i\theta})\, d\theta \qquad \text{whenever} \quad \overline{\Delta_r(a)} \subset U .\]
- An upper-semicontinuous function \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is subharmonic if and only if \[f(a) \leq \frac{1}{2\pi} \int_0^{2\pi} f(a+re^{i\theta})\, d\theta \qquad \text{whenever} \quad \overline{\Delta_r(a)} \subset U .\]
For the sub-mean-value property you may have to use the Lebesgue integral to integrate an upper-semicontinuous function, and to use the version of the Poisson integral above, you need to approximate by continuous functions on the boundary in the right way. On first reading, feel free to think of continuous subharmonic functions and not too much will be lost.
Fill in the details of the proof of Proposition \(\PageIndex{1}\).
Let \(U \subset \mathbb{C}\) be open. Show that if \(f \colon U \to \mathbb{R} \cup\{- \infty \}\) is subharmonic, then \[\limsup_{w \to z} f(w) = f(z) \qquad \text{for all $z \in U$.}\]
Suppose \(U \subset \mathbb{C}\) is open and \(g \colon U \to \mathbb{R}\) is harmonic. Then \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is subharmonic if and only if \(f-g\) is subharmonic.
Suppose \(U \subset \mathbb{C}\) is a domain and \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is subharmonic. If \(f\) attains a maximum in \(U\), then \(f\) is constant.
- Proof
-
Suppose \(f\) attains a maximum at \(a \in U\). If \(\overline{\Delta_r(a)} \subset U\), then \[f(a) \leq \frac{1}{2\pi} \int_0^{2\pi} f(a+re^{i\theta})\, d\theta \leq f(a) .\] Hence, \(f = f(a)\) almost everywhere on \(\partial \Delta_r(a)\). By upper-semicontinuity, \(f = f(a)\) everywhere on \(\partial \Delta_r(a)\). This was true for all \(r\) with \(\overline{\Delta_r(a)} \subset U\), so \(f=f(a)\) on \(\Delta_r(a)\), and so the set where \(f=f(a)\) is open. The set where an upper-semicontinuous function attains a maximum is closed. So \(f=f(a)\) on \(U\) as \(U\) is connected.
Prove that subharmonicity is a local property. That is, given an open set \(U \subset \mathbb{C}\), a function \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is subharmonic if and only if for every \(p \in U\) there exists a neighborhood \(W\) of \(p\), \(W \subset U\), such that \(f|_{W}\) is subharmonic. Hint: Perhaps try to use the maximum principle and Exercise \(\PageIndex{10}\).
Suppose \(U \subset \mathbb{C}\) is a bounded open set, \(f \colon \overline{U} \to \mathbb{R} \cup \{-\infty\}\) is an upper-semicontinuous function, such that \(f|_U\) is subharmonic, \(g \colon \overline{U} \to \mathbb{R}\) is a continuous function such that \(g|_U\) is harmonic and \(f(z) \leq g(z)\) for all \(z \in \partial U\). Prove that \(f(z) \leq g(z)\) for all \(z \in U\).
Let \(g\) be a function harmonic on a disc \(\Delta \subset \mathbb{C}\) and continuous on \(\overline{\Delta}\). Prove that for every \(\epsilon > 0\) there exists a function \(g_\epsilon\), harmonic in a neighborhood of \(\overline{\Delta}\), such that \(g(z) \leq g_\epsilon(z) \leq g(z)+\epsilon\) for all \(z \in \overline{\Delta}\). In particular, to test subharmonicity, we only need to consider those \(g\) that are harmonic a bit past the boundary of the disc.
Suppose \(U \subset \mathbb{C}\) is an open set and \(f \colon U \to \mathbb{R}\) is a \(C^2\) function. The function \(f\) is subharmonic if and only if \(\nabla^2 f \geq 0\).
- Proof
-
Suppose \(f\) is a \(C^2\)-smooth function on a subset of \(\mathbb{C} \cong \mathbb{R}^2\) with \(\nabla^2 f \geq 0\). We wish to show that \(f\) is subharmonic. Take a disc \(\Delta\) such that \(\overline{\Delta} \subset U\). Consider a function \(g\) continuous on \(\overline{\Delta}\), harmonic on \(\Delta\), and such that \(f \leq g\) on the boundary \(\partial \Delta\). Because \(\nabla^2 (f-g) = \nabla^2 f \geq 0\), we assume \(g = 0\) and \(f \leq 0\) on the boundary \(\partial \Delta\).
Suppose \(\nabla^2 f > 0\) at all points on \(\Delta\). Suppose \(f\) attains a maximum in \(\Delta\), call this point \(p\). The Laplacian \(\nabla^2 f\) is the trace of the Hessian matrix, but for \(f\) to have a maximum, the Hessian must have only nonpositive eigenvalues at the critical points, which is a contradiction as the trace is the sum of the eigenvalues. So \(f\) has no maximum inside, and therefore \(f \leq 0\) on all of \(\overline{\Delta}\).
Next suppose \(\nabla^2 f \geq 0\). Let \(M\) be the maximum of \(x^2+y^2\) on \(\overline{\Delta}\). Take \(f_n(x,y) = f(x,y) + \frac{1}{n} ( x^2+y^2 ) - \frac{1}{n}M\). Clearly \(\nabla^2 f_n > 0\) everywhere on \(\Delta\) and \(f_n \leq 0\) on the boundary, so \(f_n \leq 0\) on all of \(\overline{\Delta}\). As \(f_n \to f\), we obtain that \(f \leq 0\) on all of \(\overline{\Delta}\).
The other direction is left as an exercise.
Finish the proof of the proposition above.
In analogy to convex functions, a \(C^2\)-smooth function \(f\) of one real variable is convex if and only if \(f''(x) \geq 0\) for all \(x\).
Suppose \(U \subset \mathbb{C}\) is an open set and \(f_\alpha \colon U \to \mathbb{R} \cup \{ -\infty \}\) is a family of subharmonic functions. Let \[\varphi(z) = \sup_\alpha\, f_\alpha(z) . \] If the family is finite, then \(\varphi\) is subharmonic. If the family is infinite, \(\varphi(z) \not= \infty\) for all \(z\), and \(\varphi\) is upper-semicontinuous, then \(\varphi\) is subharmonic.
- Proof
-
Suppose \(\overline{\Delta_r(a)} \subset U\). For any \(\alpha\), \[\frac{1}{2\pi} \int_0^{2\pi} \varphi (a+re^{i\theta})\, d\theta \geq \frac{1}{2\pi} \int_0^{2\pi} f_\alpha (a+re^{i\theta})\, d\theta \geq f_\alpha(a) .\] Taking the supremum on the right over \(\alpha\) obtains the results.
Prove that if \(\varphi \colon \mathbb{R} \to \mathbb{R}\) is a monotonically increasing convex function, \(U \subset \mathbb{C}\) is an open set, and \(f \colon U \to \mathbb{R}\) is subharmonic, then \(\varphi \circ f\) is subharmonic.
Let \(U \subset \mathbb{C}\) be open, \(\{ f_n \}\) a sequence of subharmonic functions uniformly bounded above on compact subsets, and \(\{ c_n \}\) a sequence of positive real numbers such that \(\sum_{n=1}^\infty c_n < \infty\). Prove that \(f = \sum_{n=1}^\infty c_n f_n\) is subharmonic. Make sure to prove the function is upper-semicontinuous.
Suppose \(U \subset \mathbb{C}\) is a bounded open set, and \(\{ p_n \}\) a sequence of points in \(U\). For \(z \in U\), define \(f(z) = \sum_{n=1}^\infty 2^{-n} \log |z-p_n|\), possibly taking on the value \(-\infty\).
- Show that \(f\) is a subharmonic function in \(U\).
- If \(U = \mathbb{D}\) and \(p_n = \frac{1}{n}\), show that \(f\) is discontinuous at 0 (the natural topology on \(\mathbb{R} \cup \{ -\infty \}\)).
- If \(\{ p_n \}\) is dense in \(U\), show that \(f\) is discontinuous on a dense set. Hint: Prove that \(f^{-1}(-\infty)\) is a small (but dense) set. Another hint: Integrate the partial sums, and use polar coordinates.
There are too many harmonic functions in \(\mathbb{C}^n \cong \mathbb{R}^{2n}\). The real and imaginary parts of holomorphic functions in \(\mathbb{C}^n\) form a smaller set when \(n > 1\). Notice that when a holomorphic function is restricted to a complex line, we obtain a holomorphic function of one variable. So the real and imaginary parts of a holomorphic function had better be harmonic on every complex line. It turns out, this is precisely the right class of functions.
Let \(U \subset \mathbb{C}^n\) be open. A \(C^2\)-smooth \(f \colon U \to \mathbb{R}\) is pluriharmonic if for every \(a,b \in \mathbb{C}^n\), the function of one variable \[\xi \mapsto f(a+b\xi)\] is harmonic (on the set of \(\xi \in \mathbb{C}\) where \(a+b\xi \in U\)). That is, \(f\) is harmonic on every complex line.
A function \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is plurisubharmonic, sometimes plush or psh for short, if it is upper-semicontinuous and for every \(a,b \in \mathbb{C}^n\), the function of one variable \[\xi \mapsto f(a+b\xi)\] is subharmonic (whenever \(a+b\xi \in U\)).
A harmonic function of one complex variable is in some sense a generalization of an affine linear function of one real variable. Similarly, as far as several complex variables are concerned, a pluriharmonic function is the right generalization to \(\mathbb{C}^n\) of an affine linear function on \(\mathbb{R}^n\). In the same way plurisubharmonic functions are the correct complex variable generalizations of convex functions. A convex function of one real variable is like a subharmonic function, and a convex function of several real variables is a function that is convex when restricted to any real line.
Let \(U \subset \mathbb{C}^n\) be open. Prove that a \(C^2\)-smooth \(f \colon U \to \mathbb{R}\) is pluriharmonic if and only if \[\frac{\partial^2 f}{\partial \bar{z}_j \partial z_k} = 0 \quad \text{ on $U$ for all $j,k=1,\ldots,n$.}\]
Show that a pluriharmonic function is harmonic. On the other hand, find an example of a harmonic function that is not pluriharmonic.
Let \(U \subset \mathbb{C}^n\) be open. Show that \(f \colon U \to \mathbb{R}\) is pluriharmonic if and only if it is locally the real or imaginary part of a holomorphic function. Hint: Using a previous exercise \(\frac{\partial f}{\partial z_k}\) is holomorphic for all \(k\). Assume that \(U\) is simply connected, \(p \in U\), and \(f(p) = 0\). Consider the line integral from \(p\) to a nearby \(q \in U\): \[F(q) = \int_{p}^q \sum_{k=1}^n \frac{\partial f}{\partial z_k}(\zeta) \, d\zeta_k . \] Prove that it is path independent, compute derivatives of \(F\), and find out what is \(F+\bar{F}-f\).
Prove the maximum principle: If \(U \subset \mathbb{C}^n\) is a domain and \(f \colon U \to \mathbb{R} \cup \{-\infty\}\) is plurisubharmonic and achieves a maximum at \(p \in U\), then \(f\) is constant.
Let \(U \subset \mathbb{C}^n\) be open. A \(C^2\)-smooth \(f \colon U \to \mathbb{R}\) is plurisubharmonic if and only if the complex Hessian matrix \[\left[ \frac{\partial^2 f}{\partial \bar{z}_j \partial z_k} \right]_{jk}\] is positive semidefinite at every point.
- Proof
-
First suppose that the complex Hessian has a negative eigenvalue at a point \(p \in U\). After a translation assume \(p=0\). As \(f\) is real-valued, the complex Hessian \(\left[ \frac{\partial^2 f}{\partial \bar{z}_j \partial z_k} \Big|_0 \right]_{jk}\) is Hermitian. A complex linear change of coordinates acts on the complex Hessian by \(*\)-congruence, and therefore we can diagonalize, using Sylvester’s Law of Inertia again. So assume that \(\left[ \frac{\partial^2 f}{\partial \bar{z}_j \partial z_k} \Big|_0 \right]_{jk}\) is diagonal. If the complex Hessian has a negative eigenvalue, then one of the diagonal entries is negative. Without loss of generality suppose \(\frac{\partial^2 f}{\partial \bar{z}_1 \partial z_1}\Big|_0 < 0\). The function \(z_1 \mapsto f(z_1,0,\ldots,0)\) has a negative Laplacian and therefore is not subharmonic, and thus \(f\) itself is not plurisubharmonic.
For the other direction, suppose the complex Hessian is positive semidefinite at all points. Let \(p \in U\). After an affine change of coordinates assume that the line \(\xi \mapsto a+b\xi\) is simply setting all but the first variable to zero, that is, \(a=0\) and \(b=(1,0,\ldots,0)\). As the complex Hessian is positive semidefinite, \(\frac{\partial^2 f}{\partial \bar{z}_1 \partial z_1} \geq 0\) for all points \((z_1,0,\ldots,0)\). We proved above that \(\nabla^2 g \geq 0\) implies \(g\) is subharmonic, and we are done.
Suppose \(U \subset \mathbb{C}^n\) is open and \(f \colon U \to \mathbb{C}\) is holomorphic.
- Show \(\log |f(z)|\) is plurisubharmonic. In fact, it is pluriharmonic away from the zeros of \(f\).
- Show \(|f(z)|^{\eta}\) is plurisubharmonic for all \(\eta > 0\).
Show that the set of plurisubharmonic functions on an open set \(U \subset \mathbb{C}^n\) is a cone in the sense that if \(a,b > 0\) are constants and \(f, g \colon U \to \mathbb{R} \cup \{ -\infty \}\) are plurisubharmonic, then \(a f + b g\) is plurisubharmonic.
Suppose \(U \subset \mathbb{C}^n\) is an open set and \(f \colon U \to \mathbb{R} \cup \{ -\infty \}\) is plurisubharmonic. For every \(\epsilon > 0\), let \(U_\epsilon \subset U\) be the set of points further than \(\epsilon\) away from \(\partial U\). Then there exists a smooth plurisubharmonic function \(f_\epsilon \colon U_\epsilon \to \mathbb{R}\) such that \(f_\epsilon(z) \geq f(z)\), and \[f(z) = \lim_{\epsilon \to 0} f_\epsilon(z) \qquad \text{for all $z \in U$}.\]
That is, \(f\) is a limit of smooth plurisubharmonic functions. The idea of the proof is important and useful in many other contexts.
- Proof
-
We smooth \(f\) out by convolving with so-called mollifiers, or approximate delta functions. Many different mollifiers work, but let us use a specific one for concreteness. For \(\epsilon > 0\), define \[g(z) = \begin{cases} C e^{-1/(1-||z||^2)} & \text{ if $||z|| < 1$,} \\ 0 & \text{ if $||z|| \geq 1$,} \end{cases} \qquad \text{and} \qquad g_\epsilon(z) = \frac{1}{\epsilon^{2n}} g(z/\epsilon) .\] It is left as an exercise that \(g\), and so \(g_\epsilon\), is smooth. The function \(g\) has compact support as it is only nonzero inside the unit ball. The support of \(g_\epsilon\) is the \(\epsilon\)-ball. Both are nonnegative. Choose \(C\) so that \[\int_{\mathbb{C}^n} g\, dV = 1 , \qquad \text{ and therefore } \qquad \int_{\mathbb{C}^n} g_\epsilon\, dV = 1 .\] Here \(dV\) is the volume measure. The function \(g\) only depends on \(||z||\). To get an idea of how these functions work, see Figure \(\PageIndex{3}\).
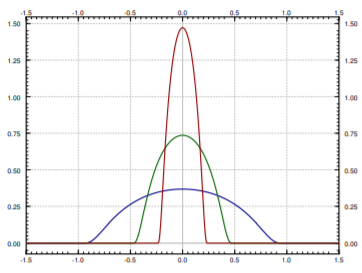
Figure \(\PageIndex{3}\)
Compare the graphs to the graphs of the Poisson kernel as a function of \(\theta\), which is also a type of mollifier. In fact, the idea of integrating against the right approximate delta function with the desired properties is similar to the solution of the Dirichlet problem using the Poisson kernel.
The function \(f\) is bounded above on compact sets as it is upper semicontinuous. If \(f\) is not bounded below, we replace \(f\) with \(\max \bigl\{ f , \frac{-1}{\epsilon} \bigr\}\), which is still plurisubharmonic. Therefore, without loss of generality we assume that \(f\) is locally bounded.
For \(z \in U_\epsilon\), we define \(f_\epsilon\) as the convolution with \(g_\epsilon\): \[f_\epsilon(z) = (f * g_\epsilon)(z) = \int_{\mathbb{C}^n} f(w) g_\epsilon (z-w) \, dV(w) = \int_{\mathbb{C}^n} f(z-w) g_\epsilon (w) \, dV(w) .\] The two forms of the integral follow easily via change of variables. We are perhaps abusing notation a bit as \(f\) is only defined on \(U\), but it is not a problem as long as \(z \in U_\epsilon\), because \(g_\epsilon\) is then zero when \(f\) is undefined. By differentiating the first form under the integral, we find that \(f_\epsilon\) is smooth.
Let us show that \(f_\epsilon\) is plurisubharmonic. We restrict to a line \(\xi \mapsto a+b\xi\). We wish to test subharmonicity by the sub-mean-value property using a circle of radius \(r\) around \(\xi = 0\): \[\begin{align}\begin{aligned} \frac{1}{2\pi} \int_0^{2\pi} f_\epsilon(a+bre^{i\theta})\, d\theta & = \frac{1}{2\pi} \int_0^{2\pi} \int_{\mathbb{C}^n} f\bigl(a+bre^{i\theta}-w\bigr) g_\epsilon (w) \, dV(w) \,d\theta \\ & = \int_{\mathbb{C}^n} \left( \frac{1}{2\pi} \int_0^{2\pi} f\bigl(a-w+bre^{i\theta}\bigr) \, d\theta \right) g_\epsilon (w) \, dV(w) \\ & \geq \int_{\mathbb{C}^n} f(a-w) g_\epsilon (w) \, dV(w) = f_\epsilon(a). \end{aligned}\end{align}\] For the inequality we used \(g_\epsilon \geq 0\). So \(f_\epsilon\) is plurisubharmonic.
Let us show that \(f_\epsilon(z) \geq f(z)\) for all \(z \in U_\epsilon\). As \(g_\epsilon(w)\) only depends on \(|w_1|,\ldots,|w_n|\), we notice that \(g_\epsilon(w_1,\ldots,w_n) = g_\epsilon(|w_1|,\ldots,|w_n|)\). Without loss of generality we consider \(z=0\), and we use polar coordinates for the integral.
\[\begin{align}\begin{aligned} f_{\epsilon}(0)&=\int_{\mathbb{C}^{n}}f(-w)g_{\epsilon}(|w_{1}|,\cdots ,|w_{n}|)dV(w) \\ &=\int_{0}^{\epsilon}\cdots\int_{0}^{\epsilon}\left(\int_{0}^{2\pi}\cdots\int_{0}^{2\pi}f(-r_{1}e^{1\theta_{i}}, \cdots ,-r_{n}e^{i\theta_{n}})d\theta_{1}\cdots d\theta_{n}\right) \\ & \qquad\qquad\qquad\qquad\qquad\qquad g_{\epsilon}(r_{1},\cdots ,r_{n})r_{1}\cdots r_{n}dr_{1}\cdots dr_{n} \\ &\geq\int_{0}^{\epsilon}\cdots\int_{0}^{\epsilon}\left(\int_{0}^{2\pi}\cdots\int_{0}^{2\pi}(2\pi )f(0, -r_{2}e^{i\theta_{2}},\cdots ,-r_{n}e^{-\theta _{n}})d\theta_{2}\cdots d\theta_{n}\right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad g_{\epsilon}(r_{1},\cdots ,r_{n})r_{1}\cdots r_{n}dr_{1}\cdots dr_{n} \\ &\geq f(0)\int_{0}^{\epsilon}\cdots\int_{0}^{\epsilon}(2\pi )^{n}g_{\epsilon}(r_{1},\cdots r_{n})r_{1}\cdots r_{n}dr_{1}\cdots dr_{n} \\ &=f(0)\int_{\mathbb{C}^{n}}g_{\epsilon}(w)dV(w)=f(0).\end{aligned}\end{align}\]
The second equality above follows as \(g_\epsilon\) is zero outside the polydisc of radius \(\epsilon\). For the inequalities, we again needed that \(g_\epsilon \geq 0\). The penultimate equality follows from the fact that \(2\pi = \int_0^{2\pi}d \theta\).
Finally, we show \(\lim_{\epsilon \to 0} f_\epsilon (z) = f(z)\). For subharmonic, and so for plurisubharmonic, functions, \(\limsup_{\zeta\to z} f(\zeta) = f(z)\). So given \(\delta >0\) find an \(\epsilon >0\) such that \(f(\zeta)-f(z) \leq \delta\) for all \(\zeta \in B_\epsilon(z)\). \[\begin{align}\begin{aligned} f_\epsilon(z) - f(z) & = \int_{B_\epsilon(0)} f(z-w) g_\epsilon (w) \, dV(w) - f(z) \int_{B_\epsilon(0)} g_\epsilon (w) \, dV(w) \\ & = \int_{B_\epsilon(0)} \bigl(f(z-w)-f(z)\bigr)\, g_\epsilon (w) \, dV(w) \\ & \leq \delta \int_{B_\epsilon(0)} g_\epsilon (w) \, dV(w) = \delta . \end{aligned}\end{align}\] Again we used that \(g_\epsilon \geq 0\). We find \(0 \leq f_\epsilon - f(z) \leq \delta\), and so \(f_\epsilon(z) \to f(z)\).
Show that \(g\) in the proof above is smooth on all of \(\mathbb{C}^n\).
- Show that for a subharmonic function \(f\), \(\int_0^{2\pi} f(a+re^{i\theta}) \, d\theta\) is a monotone function of \(r\). Hint: Try a \(C^2\) function first and use Green’s theorem.
- Use this fact to show that the \(f_\epsilon(z)\) from Theorem \(\PageIndex{2}\) is monotone decreasing in \(\epsilon\).
Let \(U \subset \mathbb{C}^n\) and \(V \subset \mathbb{C}^m\) be open. Prove that if \(g \colon U \to V\) is holomorphic and \(f \colon V \to \mathbb{R}\) is a \(C^2\) plurisubharmonic function, then \(f \circ g\) is plurisubharmonic. Then use it to prove the same fact for all plurisubharmonic functions (Hint: monotone convergence).
Show that plurisubharmonicity is a local property, that is, \(f\) is plurisubharmonic if and only if \(f\) is plurisubharmonic in some neighborhood of each point.
Using the computation from Theorem \(\PageIndex{2}\) show that if \(f\) is pluriharmonic, then \(f_\epsilon = f\) (where it makes sense), obtaining another proof that a pluriharmonic function is \(C^\infty\).
Let the \(f\) in Theorem \(\PageIndex{2}\) be continuous and suppose \(K \subset \subset U\). For small enough \(\epsilon >0\), \(K \subset U_\epsilon\). Show that \(f_\epsilon\) converges uniformly to \(f\) on \(K\).
Let the \(f\) in Theorem \(\PageIndex{2}\) be \(C^k\)-smooth for some \(k \geq 0\). Show that all derivatives of \(f_\epsilon\) up to order \(k\) converge uniformly on compact sets to the corresponding derivatives of \(f\). See also previous exercise.
Let us prove the theorem of Radó, which is a complementary result to the Riemann extension theorem. Here on the one hand the function is continuous and vanishes on the set you wish to extend across, but on the other hand you know nothing about this set. It is sometimes covered in a one-variable course, and in several variables it follows directly from the one-variable result.
Let \(U \subset \mathbb{C}^n\) be open and \(f \colon U \to \mathbb{C}\) a continuous function that is holomorphic on the set \[U' = \bigl\{ z \in U : f(z) \not= 0 \bigr\} . \] Then \(f \in \mathcal{O}(U)\).
- Proof
-
First assume \(n=1\). As the theorem is local, it is enough to prove it for a small disc \(\Delta\) such that \(f\) is continuous on the closure \(\overline{\Delta}\), let \(\Delta'\) be the part of the disc where \(f\) is nonzero. If \(\Delta'\) is empty, then we are done as \(f\) is just identically zero and hence holomorphic.
Let \(u\) be the real part of \(f\). On \(\Delta'\), \(u\) is a harmonic function. Let \(Pu\) be the Poisson integral of \(u\) on \(\Delta\). Hence \(Pu\) equals \(u\) on \(\partial \Delta\), and \(Pu\) is harmonic in all of \(\Delta\). Consider the function \(Pu(z) - u(z)\) on \(\overline{\Delta}\). The function is zero on \(\partial \Delta\) and it is harmonic on \(\Delta'\). By rescaling \(f\) we can without loss of generality assume that \(|f(z)| < 1\) for all \(z \in \overline{\Delta}\). For any \(t >0\), the function \(z \mapsto t \log |f(z)|\) is subharmonic on \(\Delta'\) and upper-semicontinuous on \(\overline{\Delta'}\). Further, it is negative on \(\partial \Delta\). The function \(z \mapsto -t \log |f(z)|\) is superharmonic (minus a subharmonic function) on \(\Delta'\), lower-semicontinuous on \(\overline{\Delta'}\) and positive on \(\partial \Delta\). On the set \(\Delta \setminus \Delta'\) where \(f\) is zero, the two functions are \(-\infty\) and \(\infty\) respectively. See Figure \(\PageIndex{4}\). Therefore, for all \(t > 0\) and \(z \in \partial \Delta \cup (\Delta \setminus \Delta')\), we have \[\label{eq:3} t \log |f(z)| \leq Pu(z)-u(z) \leq -t \log |f(z)| .\] Applying the maximum principle to the subharmonic functions \(z \mapsto t \log |f(z)| - \bigl(Pu(z)-u(z)\bigr)\) and \(z \mapsto t \log |f(z)| - \bigl(u(z)-Pu(z)\bigr)\) shows that \(\eqref{eq:3}\) holds for all \(z \in \Delta'\) and all \(t > 0\).
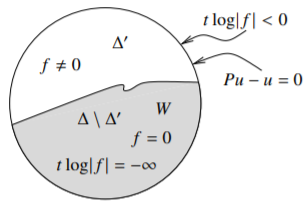
Figure \(\PageIndex{4}\)
Taking the limit \(t \to 0\) shows that \(Pu = u\) on \(\Delta'\). Let \(W = \Delta \setminus \overline{\Delta'}\). On \(W\), \(u=0\) and so \(Pu-u\) is harmonic on \(W\) and continuous on \(\overline{W}\). Furthermore, \(Pu-u=0\) on \(\overline{\Delta'} \cup \partial \Delta\), and so \(Pu-u=0\) on \(\partial W\). By the maximum principle, \(Pu=u\) on \(W\) and therefore on all of \(\overline{\Delta}\). Similarly, if \(v\) is the imaginary part of \(f\), then \(Pv = v\) on \(\overline{\Delta}\). In other words, \(u\) and \(v\) are harmonic on \(\Delta\). As \(\Delta\) is simply connected, let \(\tilde{v}\) be the harmonic conjugate of \(u\) that equals \(v\) at some point of \(\Delta'\). As \(f\) is holomorphic on \(\Delta'\), the harmonic functions \(\tilde{v}\) and \(v\) are equal the nonempty open subset \(\Delta'\) of \(\Delta\) and so they are equal everywhere. Consequently, \(f = u +iv\) is holomorphic on \(\Delta\).
The extension of the proof to several variables is left as an exercise.
Use the one-variable result to extend the theorem to several variables.


