高等数学常用曲线(四)——双纽线

声明：本篇幅系全网首篇关于双纽线相关数据计算方面最详细总结！关于双纽线3种旋转体积的计算过程、推理方法由本人原创，盗版必究！

声明：本篇幅仅在知乎发布，严禁转载、抄袭！

声明*：关于双纽线3种旋转体积的计算过程和自创方法皆由本人在草稿纸上经过数次严格验算后得出。若本人自创的方法与其ta创作者的方法有雷同之处，请谅解！

(声明于：Jan 17, 2023)

注*：强烈建议读者、网友们在PC端、平板...上进行浏览阅读，以获得更佳阅读浏览体验。

注*：相对于高等数学或考研数学而言，本篇幅将出现大量超纲内容。望读者根据自己的水平，选择性地吸收！

创作于----Dec 28, 2022

更新于----Jun 22, 2023

关于第一期与本系列篇幅专栏见如下链接。

如果对你有帮助，请不忘收藏、点赞或转发给身边需要帮助的同学。

四、伯努利双纽线(lemniscate)

定义：设直线段AB的长度为2a，记A、B坐标分别为(-a,0)、(a,0)，若有一动点P(x,y)满足|PA|·|PB|=a²，那么点P的轨迹就是伯努利双纽线。见图1所示。

按照定义，可得出双纽线的直角坐标形式，这里就省去推导流程。

\displaystyle (x^2+y^2)^2=2a^2(x^2-y^2)

进而得到极坐标方程，

\displaystyle r^2=2a^2cos2\theta

事实上，以上两个形式并不是我们平时做题时经常遇到的。其实，稍微把上述定义修改一下就可以实现。

即把定义中的a替换成a/√2即可。

注*：接下来的图像、表达式以及相关的曲线数据计算都采用修改后的定义。

1.图像与表达式

1.⑴图像

1.⑴表达式

极坐标：

\displaystyle r^2=a^2cos2\theta

\displaystyle \theta\in[-\frac{\pi}{4},\frac{\pi}{4}]\cup[\frac{3\pi}{4},\frac{5\pi}{4}],a>0

直角坐标：

\displaystyle (x^2+y^2)^2=a^2(x^2-y^2),a>0

1.⑵图像

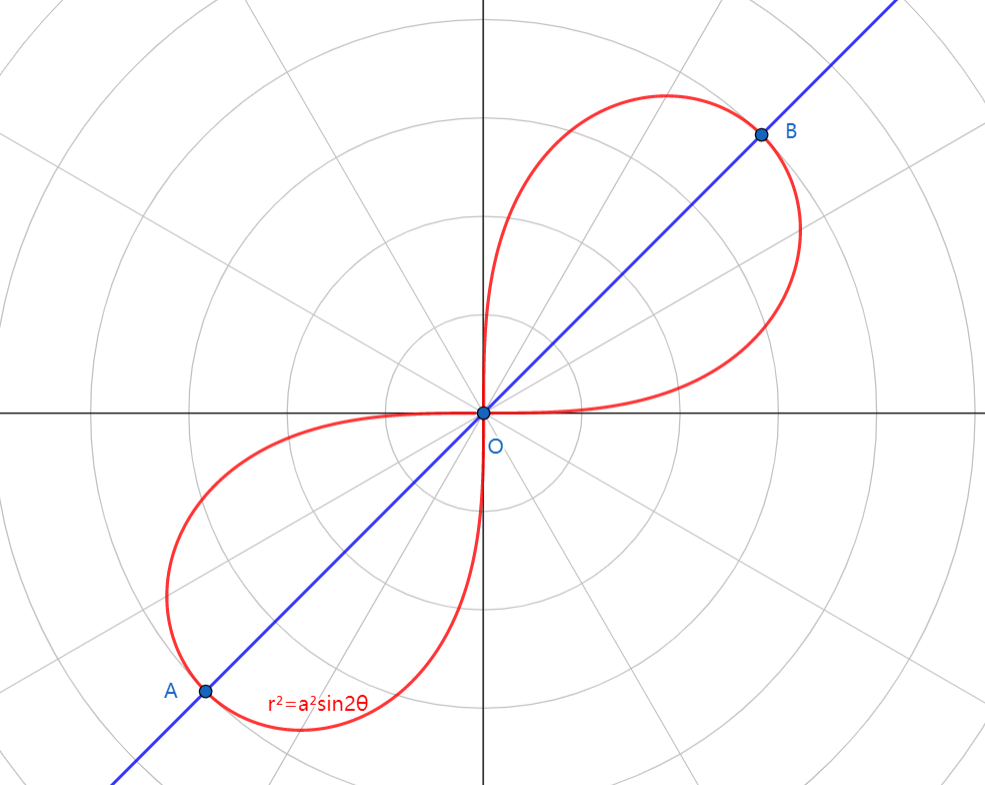
1.⑵表达式

极坐标：

\displaystyle r^2=a^2sin2\theta

\displaystyle\theta\in[0,\frac{\pi}{2}]\cup[\pi,\frac{3\pi}{2}],a>0

直角坐标：

\displaystyle (x^2+y^2)^2=2a^2xy,a>0

在本系列篇幅第一期中介绍了极坐标的旋转变换，那么由图2变成图3，就相当于把图2逆时针旋转45°。

\displaystyle pic2:r^2=a^2cos2\theta\rightarrow r^2=a^2cos2(\theta-\frac{\pi}{4})

\displaystyle \rightarrow r^2=a^2cos(2\theta-\frac{\pi}{2})

\rightarrow pic3:r^2=a^2sin2\theta

接下来关于双纽线相关数据计算，只考虑采用极坐标形式。

在计算整条曲线弧长、面积、旋转体积、旋转表面积之前优先考虑其对称性。

2.弧长

记图2的弧长为L，其中

\displaystyle r'=-\frac{a\cdot sin2\theta}{\sqrt{cos2\theta}}

\displaystyle L=4\int_{0}^{\frac{\pi}{4}}\sqrt{r^2(\theta)+[r'(\theta)]^2}d\theta

\displaystyle =4\int_{0}^{\frac{\pi}{4}}\sqrt{a^2cos2\theta+a^2\cdot\frac{sin^22\theta}{cos2\theta} }d\theta

\displaystyle =4a\int_{0}^{\frac{\pi}{4}}\sqrt{cos2\theta+\frac{sin^22\theta}{cos2\theta} }d\theta

\displaystyle =4a\int_{0}^{\frac{\pi}{4}}\sqrt{\frac{cos^22\theta}{cos2\theta}+\frac{sin^22\theta}{cos2\theta} }d\theta

\displaystyle =4a\int_{0}^{\frac{\pi}{4}}\sqrt{\frac{1}{cos2\theta} }d\theta

\displaystyle =4a\int_{0}^{\frac{\pi}{4}}\sqrt{sec2\theta }d\theta

\displaystyle =2a\int_{0}^{\frac{\pi}{2}}\sqrt{secu }du

\displaystyle =2a\int_{0}^{\frac{\pi}{2}}cos^{-\frac{1}{2}}udu

\displaystyle =2a\cdot\frac{\Gamma(\frac{1}{2})\Gamma(\frac{1}{4})}{2\Gamma(\frac{3}{4})}

\displaystyle =\frac{\sqrt{\pi}\cdot\Gamma(\frac{1}{4})}{\Gamma(\frac{3}{4})}a\approx 5.244a

其中，

\displaystyle \Gamma(\frac{1}{4})=\frac{\Gamma(1.25)}{0.25}=\frac{0.9064}{0.25}\approx 3.6256

\displaystyle \Gamma(\frac{3}{4})=\frac{\Gamma(1.75)}{0.75}=\frac{0.91906}{0.75}\approx 1.2254

\displaystyle \sqrt{\pi}\approx 1.7725

注1：此弧长积分并非初等积分，因此结果可以保留gamma函数值的形式。

注2：上述定积分计算中用到了一类定积分的结论。此结论大致证明见本篇幅后半部分。

\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{\alpha}\theta \cdot cos^{\beta}\theta d\theta=\frac{\Gamma(\frac{1+\alpha}{2})\Gamma(\frac{1+\beta}{2})}{2\Gamma(1+\frac{\alpha+\beta}{2})}

\displaystyle (\alpha、\beta>-1，\alpha\in R，\beta\in R)

特别地，当α、β为正整数时，可得出更为广泛的华里士公式结论。

注3：计算结果中的两个gamma函数值用到了递推公式，gamma函数的递推公式也见本篇幅后半部分，且特殊值经过查表后得出其近似值。

3.面积

对于双纽线，考虑封闭图形的面积。

记图2双纽线围成的面积为A1，按照对称性，

\displaystyle A_1=2\cdot \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\frac{1}{2}[r(\theta)]^2d\theta

\displaystyle=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}r^{2}(\theta)d\theta

\displaystyle=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}a^2cos2\theta d\theta

\displaystyle=2a^2\int_{0}^{\frac{\pi}{4}}cos2\theta d\theta

\displaystyle=a^2\int_{0}^{\frac{\pi}{4}}cos2\theta d(2\theta)

=a^2\cdot sin(2\theta)|_{0}^{\frac{\pi}{4}}

=a^2

或者记图3双纽线面积为A2，按照对称性，

\displaystyle A_{2}=2\cdot \int_{0}^{\frac{\pi}{2}}\frac{1}{2}[r(\theta)]^2d\theta

\displaystyle =\int_{0}^{\frac{\pi}{2}}[r(\theta)]^2d\theta

\displaystyle=\int_{0}^{\frac{\pi}{2}}a^2sin2\theta d\theta

\displaystyle=a^2\int_{0}^{\frac{\pi}{2}}sin2\theta d\theta

=a^2

4.旋转体积

计算前，先给出图2双纽线绕极轴旋转所产生的图形，如下图4所示。

同理，图2双纽线绕垂直于极轴(y轴)旋转产生的图形，见下图5所示。

注：以上图4、图5来源于：

还是分曲线绕x轴、y轴两种情况讨论。这里，先引入以下两个重要结论。

*NOTE→极坐标曲线的旋转体积

①极坐标曲线r(θ)绕极轴旋转一周形成的空间图形的体积，

其中： 0\leq\alpha\leq\theta\leq\beta\leq\pi,0\leq r\leq r(\theta)

\displaystyle V=\frac{2\pi}{3}\int_{\alpha}^{\beta}r^3(\theta)sin\theta d\theta

②极坐标曲线r(θ)绕垂直于极轴旋转一周形成的空间图形的体积，

其中： \displaystyle -\frac{\pi}{2}\leq\alpha\leq\theta\leq\beta\leq\frac{\pi}{2},0\leq r\leq r(\theta)

\displaystyle V=\frac{2\pi}{3}\int_{\alpha}^{\beta}r^3(\theta)cos\theta d\theta

注1：关于极坐标旋转体积公式，可用二重积分求旋转体积的思想来大致证明。

注2：以下计算双纽线旋转体积的原创方法和过程皆由本人在草稿纸上严格推导而出。若本人自创方法与其ta创作者的方法有雷同之处，请谅解！

(声明于：Jan 17, 2023)

4.1情况一

记图2双纽线绕x轴旋转一周形成的图形体积为Vx，则

\displaystyle V_{x}=2\cdot \frac{2\pi}{3}\int_{0}^{\frac{\pi}{4}}r^3(\theta)sin\theta d\theta

\displaystyle =\frac{4\pi}{3}\int_{0}^{\frac{\pi}{4}}a^3cos^{\frac{3}{2}}2\theta \cdot sin\theta d\theta

\displaystyle =\frac{4\pi a^3}{3}\int_{0}^{\frac{\pi}{4}}cos^{\frac{3}{2}}2\theta \cdot sin\theta d\theta

\displaystyle =\frac{4\pi a^3}{3}I

\displaystyle I=\int_{0}^{\frac{\pi}{4}}cos^{\frac{3}{2}}2\theta \cdot sin\theta d\theta

\displaystyle =-\int_{0}^{\frac{\pi}{4}}(2cos^2\theta-1)^{\frac{3}{2}} d(cos\theta)

\displaystyle =\int_{\frac{\sqrt2}{2}}^{1}(2u^2-1)^{\frac{3}{2}} du

\displaystyle =\int_{\frac{\sqrt2}{2}}^{1}[(\sqrt{2}u)^2-1]^{\frac{3}{2}} du

\displaystyle =\frac{\sqrt2}{2}\int_{0}^{\frac{\pi}{4}}tan^4\alpha sec\alpha d\alpha(\sqrt2u=sec\alpha)

\displaystyle =\frac{\sqrt2}{2}\int_{0}^{\frac{\pi}{4}}(sec^2\alpha-1)^2 sec\alpha d\alpha

\displaystyle =\frac{\sqrt2}{2}\int_{0}^{\frac{\pi}{4}}(sec^5\alpha+sec\alpha-2sec^3\alpha)d\alpha

于是讨论在计算过程中出现的两个不定积分的结果，

先计算的sec^{3}\alpha的不定积分，

\displaystyle\int sec^3\alpha d\alpha

\displaystyle=\int sec^2\alpha ·sec\alpha d\alpha

\displaystyle=\int sec\alpha d(tan\alpha)

\displaystyle=sec\alpha·tan\alpha-\int tan\alpha d(sec\alpha)

\displaystyle=sec\alpha·tan\alpha-\int tan^2\alpha·sec\alpha d\alpha

\displaystyle=sec\alpha·tan\alpha-\int (sec^2\alpha-1)·sec\alpha d\alpha

\displaystyle=sec\alpha·tan\alpha-\int sec^3\alpha d\alpha+\int sec\alpha d\alpha

移项可得，

\displaystyle\int sec^3\alpha d\alpha=\frac{1}{2}(sec\alpha·tan\alpha+\int sec\alpha d\alpha)

\displaystyle=\frac{1}{2}(sec\alpha ·tan\alpha+ln\left| sec\alpha+tan\alpha \right|)+C

注：建议读者记住sec^{3}\alpha的不定积分结果。

再计算sec^5\alpha的不定积分，

\displaystyle \int sec^{5}\alpha d\alpha=\int sec^{3}\alpha \cdot sec^2\alpha d\alpha

\displaystyle =\int sec^{3}\alpha d(tan\alpha)

\displaystyle =sec^{3}\alpha \cdot tan\alpha-\int tan\alpha d(sec^3\alpha)

\displaystyle =sec^{3}\alpha \cdot tan\alpha-3\int sec^3\alpha \cdot tan^{2}\alpha d\alpha

\displaystyle =sec^{3}\alpha \cdot tan\alpha-3\int sec^3\alpha \cdot (sec^2\alpha-1) d\alpha

\displaystyle =sec^{3}\alpha \cdot tan\alpha-3\int sec^5\alpha d\alpha+3\int sec^3\alpha d\alpha

移项可得，

\displaystyle \int sec^{5}\alpha d\alpha=\frac{1}{4}sec^{3}\alpha \cdot tan\alpha+\frac{3}{4}\int sec^3\alpha d\alpha

\displaystyle =\frac{1}{4}sec^{3}\alpha \cdot tan\alpha+\frac{3}{8}(sec\alpha ·tan\alpha+ln\left| sec\alpha+tan\alpha \right|)+C

于是代入积分上下限，得

\displaystyle \int_{0}^{\frac{\pi}{4}}sec^5\alpha d\alpha=\frac{7\sqrt2}{8}+\frac{3}{8}ln(\sqrt2+1)

\displaystyle \int_{0}^{\frac{\pi}{4}}sec\alpha d\alpha=ln(\sqrt2+1)

\displaystyle \int_{0}^{\frac{\pi}{4}}sec^3\alpha d\alpha=\frac{\sqrt2}{2}+\frac{1}{2}ln(\sqrt2+1)

\displaystyle \therefore I=\frac{\sqrt2}{2}[\frac{3}{8}ln(\sqrt2+1)-\frac{\sqrt2}{8}]

\displaystyle \therefore V_{x}=\frac{4\pi a^3}{3}I=[\frac{\sqrt2}{4}ln(\sqrt2+1)-\frac{1}{6}]\pi a^3

注：不定积分代入积分上下限时，不用在乎常数C的影响。因为上下限是关于α的积分，代入上、下限后，常数C无变化，然后在上限减去下限的过程中，常数C会被抵消掉。

关于计算sec^3\alpha、 sec^5\alpha的不定积分方法来源于本人主页专栏的同济七版积分表公式推理中的第二篇。

4.2情况二

记图2双纽线绕y轴旋转一周形成的图形体积为Vy，则

\displaystyle V_{y}=2\cdot \frac{2\pi}{3}\int_{0}^{\frac{\pi}{4}}r^3(\theta)cos\theta d\theta

\displaystyle =\frac{4\pi}{3}\int_{0}^{\frac{\pi}{4}}a^3cos^{\frac{3}{2}}2\theta \cdot cos\theta d\theta

\displaystyle =\frac{4\pi a^3}{3}\int_{0}^{\frac{\pi}{4}}cos^{\frac{3}{2}}2\theta \cdot cos\theta d\theta

\displaystyle =\frac{4\pi a^3}{3}I

\displaystyle I=\int_{0}^{\frac{\pi}{4}}cos^{\frac{3}{2}}2\theta \cdot cos\theta d\theta

\displaystyle =\int_{0}^{\frac{\pi}{4}}(1-2sin^2\theta)^{\frac{3}{2}} d(sin\theta)

\displaystyle =\int_{0}^{\frac{\sqrt2}{2}}(1-2u^2)^{\frac{3}{2}} du

\displaystyle=\int_{0}^{\frac{\sqrt2}{2}}[1-(\sqrt2u)^2]^{\frac{3}{2}} du

\displaystyle =\frac{\sqrt2}{2}\int_{0}^{\frac{\pi}{2}}cos^4\alpha d\alpha(\sqrt2u=sin\alpha)

\displaystyle =\frac{\sqrt2}{2}\cdot\frac{3}{4}\cdot\frac{1}{2}\cdot\frac{\pi}{2}=\frac{3\sqrt2\pi}{32}

\displaystyle \therefore V_{y}=\frac{4\pi a^3}{3}I=\frac{\pi^2a^3}{4\sqrt2}

看来Vy的计算量要远小于Vx的计算量。计算Vx的过程过于繁琐，并且在计算Vx的过程中还出现了两个不定积分公式的推导。

若不知道在极坐标下曲线绕x、y轴的旋转体积公式，而是将双纽线的极坐标形式转化为参数方程进行计算的话，那计算量将变得更为复杂。

在计算Vy的过程中，用到了经典著名的华里士(Wallis)公式，现呈现给大家。本篇幅后半部分还会为大家呈现推广的Wallis公式！

*NOTE→华里士公式：

Ⅰ、若 \displaystyle I_{n}=\int_{0}^{\frac{\pi}{2}}sin^nxdx=\int_{0}^{\frac{\pi}{2}}cos^nxdx

a.当n为大于1的正奇数

\displaystyle I_{n}=\frac{n-1}{n}·\frac{n-3}{n-2}···\frac{4}{5}·\frac{2}{3}·I_{1}(I_{1}=1)

或 \displaystyle I_{n}=\frac{(n-1)!!}{n!!}

b.当n为正偶数

\displaystyle I_{n}=\frac{n-1}{n}·\frac{n-3}{n-2}···\frac{3}{4}·\frac{1}{2}·I_{0}(I_{0}=\frac{\pi}{2})

或 \displaystyle I_{n}=\frac{(n-1)!!}{n!!}· \frac{\pi}{2}

Ⅱ、若 \displaystyle I_{n}=\int_{0}^{\pi}sin^nxdx

c.当n为大于1的正奇数

\displaystyle I_{n}=2·\frac{n-1}{n}·\frac{n-3}{n-2}···\frac{4}{5}·\frac{2}{3}·1

或 \displaystyle I_{n}=2·\frac{(n-1)!!}{n!!}

d.当n为正偶数

\displaystyle I_{n}=2·\frac{n-1}{n}·\frac{n-3}{n-2}···\frac{3}{4}·\frac{1}{2}·\frac{\pi}{2}

或 \displaystyle I_{n}=2·\frac{(n-1)!!}{n!!}· \frac{\pi}{2}

\displaystyle=\frac{(n-1)!!}{n!!}·\pi

Ⅲ、若 \displaystyle I_{n}=\int_{0}^{\pi}cos^nxdx

e.当n为正奇数： \displaystyle I_{n}=0

f.当n为正偶数

\displaystyle I_{n}=2·\frac{n-1}{n}·\frac{n-3}{n-2}···\frac{3}{4}·\frac{1}{2}·\frac{\pi}{2}

或 \displaystyle I_{n}=2·\frac{(n-1)!!}{n!!}· \frac{\pi}{2}

\displaystyle=\frac{(n-1)!!}{n!!}·\pi

Ⅳ、 \displaystyle I_{n}=\int_{0}^{2\pi}sin^nxdx=\int_{0}^{2\pi}cos^nxdx

g.当n为正奇数： \displaystyle I_{n}=0

h.当n为正偶数

\displaystyle I_{n}=4·\frac{n-1}{n}·\frac{n-3}{n-2}···\frac{3}{4}·\frac{1}{2}·\frac{\pi}{2}

或 \displaystyle I_{n}=4·\frac{(n-1)!!}{n!!}· \frac{\pi}{2}

\displaystyle=\frac{(n-1)!!}{n!!}·2\pi

4.3情况三

记图3双纽线绕x轴旋转一周形成的图形体积为Vx，则

\displaystyle V_{x}=2\cdot \frac{2\pi}{3}\int_{0}^{\frac{\pi}{2}}r^3(\theta)sin\theta d\theta

\displaystyle =\frac{4\pi}{3}\int_{0}^{\frac{\pi}{2}}a^3sin^{\frac{3}{2}}2\theta \cdot sin\theta d\theta

\displaystyle =\frac{4\pi a^3}{3}\int_{0}^{\frac{\pi}{2}}sin^{\frac{3}{2}}2\theta \cdot sin\theta d\theta

\displaystyle =\frac{4\pi a^3}{3}I

\displaystyle I=\int_{0}^{\frac{\pi}{2}}sin^{\frac{3}{2}}2\theta \cdot sin\theta d\theta

\displaystyle=2\sqrt{2}\int_{0}^{\frac{\pi}{2}}sin^{\frac{5}{2}}\theta\cdot cos^{\frac{3}{2}}\theta d\theta

\displaystyle=2\sqrt{2}I_{0}

\displaystyle I_{0}=\int_{0}^{\frac{\pi}{2}}sin^{\frac{5}{2}}\theta\cdot cos^{\frac{3}{2}}\theta d\theta

考虑I0这个定积分，这里要用到Beta函数(Β函数)与Gamma函数(Γ函数)，以及Gamma函数中的余元公式。

这两个函数统称为Euler积分，其中Beta函数称为第一类Euler积分，Gamma函数称为第二类Euler积分。这里不过多介绍这两个函数背景，大家自行了解即可。

若想解决I0定积分，得先从Beta函数基本形式入手。

\displaystyle B(p,q)=\int_{0}^{1}x^{p-1}(1-x)^{q-1}dx(p、q\in R^{+})

如何将Beta函数与I0定积分联系起来？

看到Beta函数中x、1-x相乘的形式了吗？想到令x=sin²θ，

于是得到B函数的其它含参积分形式，

\displaystyle B(p,q)=\int_{0}^{1}x^{p-1}(1-x)^{q-1}dx

\displaystyle=\int_{0}^{\frac{\pi}{2}}sin^{2(p-1)}\theta \cdot cos^{2(q-1)}\theta d(sin^{2}\theta)

\displaystyle=2\int_{0}^{\frac{\pi}{2}}sin^{2p-1}\theta \cdot cos^{2q-1}\theta d\theta

注：这里稍微总结一下B函数的形式、性质。读者了解一下就行，不作证明！

*NOTE→关于Beta函数定义、性质

(来源：华师大数分四版下册)

①B函数定义与其它形式

Ⅰ、 \displaystyle B(p,q)=\int_{0}^{1}x^{p-1}(1-x)^{q-1}dx

\displaystyle=2\int_{0}^{\frac{\pi}{2}}sin^{2p-1}\theta \cdot cos^{2q-1}\theta d\theta(x=sin^2\theta)

\displaystyle =\int_{0}^{+\infty}\frac{t^{p-1}}{(1+t)^{p+q}}dt(x=\frac{t}{1+t})

\displaystyle =\int_{0}^{1}\frac{t^{p-1}+t^{q-1}}{(1+t)^{p+q}}dt

(p、q\in R^{+})

Ⅱ、 \displaystyle \frac{1}{r}B(\frac{p}{r},q)=\int_{0}^{1}x^{p-1}(1-x^r)^{q-1}dx

(p、q、r\in R^{+})

②B函数性质

Ⅰ、对称性

\displaystyle B(p,q)=B(q,p)(p、q\in R^{+})

Ⅱ、递推公式

\displaystyle B(p,q)=\frac{q-1}{p+q-1}B(p,q-1)(p>0,q>1)

\displaystyle =\frac{p-1}{p+q-1}B(p-1,q)(p>1,q>0)

\displaystyle =\frac{(p-1)(q-1)}{(p+q-1)(p+q-2)}B(p-1,q-1)(p、q>1)

回到刚才那个话题，注意到Beta函数与Gamma函数的关系，即

\displaystyle B(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}(p、q\in R^+)

注1：证明这个关系要用到反常二重积分，详细证明过程可参见《数学分析——华师大四版下册》。由于过程太复杂，这里就不证明。

注2：一般情况下，用Γ函数的情况多于B函数。知道了B函数与Γ函数的关系，以后遇到B函数定义形式中的那几种积分，就可以转化为Γ函数去进一步计算。

于是，

\displaystyle2\int_{0}^{\frac{\pi}{2}}sin^{2p-1}\theta \cdot cos^{2q-1}\theta d\theta=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}

\displaystyle\therefore\int_{0}^{\frac{\pi}{2}}sin^{2p-1}\theta \cdot cos^{2q-1}\theta d\theta=\frac{\Gamma(p)\Gamma(q)}{2\Gamma(p+q)}

令 \displaystyle 2p-1=\alpha、2q-1=\beta ，故

\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{\alpha}\theta \cdot cos^{\beta}\theta d\theta

\displaystyle=\frac{1}{2}B(\frac{\alpha+1}{2},\frac{\beta+1}{2})

\displaystyle=\frac{\Gamma(\frac{1+\alpha}{2})\Gamma(\frac{1+\beta}{2})}{2\Gamma(1+\frac{\alpha+\beta}{2})}

\displaystyle (\alpha、\beta>-1，\alpha\in R，\beta\in R)

于是得到了这类特殊定积分的计算结论。

\displaystyle\therefore I_{0}=\int_{0}^{\frac{\pi}{2}}sin^{\frac{5}{2}}\theta\cdot cos^{\frac{3}{2}}\theta d\theta

\displaystyle=\frac{\Gamma(\frac{7}{4})\Gamma(\frac{5}{4})}{2\Gamma(3)}

\displaystyle=\frac{\frac{3}{4}\Gamma(\frac{3}{4})\cdot \frac{1}{4}\Gamma(\frac{1}{4})}{2\cdot 2!}

\displaystyle=\frac{3}{64}\cdot\Gamma(\frac{3}{4})\Gamma(\frac{1}{4})

\displaystyle=\frac{3}{64}\cdot\frac{\pi}{sin\frac{\pi}{4}}=\frac{3\sqrt{2}\pi}{64}

\displaystyle \therefore I=2\sqrt{2}I_{0}=\frac{3\pi}{16}

于是图3双纽线绕x轴的旋转体积为，

\displaystyle V_{x}=\frac{4\pi a^3}{3}I=\frac{\pi^2a^3}{4}

按照对称性，图3双纽线绕y轴的旋转体积为，

\displaystyle V_{y}=V_{x}=\frac{\pi^2a^3}{4}

注：上述在计算I0定积分的过程中用到了几个常用Γ函数的结论，现呈现给大家。

*NOTE→关于Gamma函数定义、性质、推广结论

①Γ函数定义

\displaystyle \Gamma(s)=\int_{0}^{+\infty}e^{-x}x^{s-1}dx(s>0)

\displaystyle=2\int_{0}^{+\infty}e^{-u^2}u^{2s-1}du(s>0)

\displaystyle \Gamma(\frac{s+1}{2})=2\int_{0}^{+\infty}e^{-u^2}u^sdu(s>0)

\displaystyle \Gamma(s+1)=\int_{0}^{+\infty}e^{-x}x^{s}dx(s>0)

注：Gamma函数定义的形式有多种，这里只给出常用的几种定义形式。

②递推公式： \displaystyle \Gamma(s+1)=s\Gamma(s)(s>0)

③阶乘公式： \displaystyle \Gamma(n+1)=n!(n\in N)

④余元公式：

\displaystyle \Gamma(s)\Gamma(1-s)=B(s,1-s)

\displaystyle=\int_{0}^{+\infty}\frac{x^{s-1}}{1+x}dx=\frac{\pi}{sin\pi s}(0<s<1)

⑤泊松积分： (要用到余元公式)

\displaystyle \Gamma(\frac{1}{2})=2\int_{0}^{+\infty}e^{-u^2}du

\displaystyle=\int_{-\infty}^{+\infty}e^{-u^2}du=\sqrt{\pi}

⑦双阶乘公式

(可把结果运用到华里士公式中)

Ⅰ、 \displaystyle 2\cdot4\cdot6\cdot...\cdot2n=(2n)!!

\displaystyle =2^{n}\cdot n!=2^{n}\Gamma(n+1)

(n\in N^*)

Ⅱ、 \displaystyle1\cdot3\cdot5\cdot...\cdot(2n-1)=(2n-1)!!

\displaystyle=\frac{\Gamma(2n)}{2^{n-1}\Gamma(n)}(n\in N^*)

⑧两个Γ函数等式(用到递推公式)

Ⅰ、 \displaystyle \Gamma(n+\frac{1}{2})

\displaystyle=\frac{2n-1}{2}\Gamma[\frac{1}{2}+(n-1)]

\displaystyle=\frac{2n-1}{2}\cdot\frac{2n-3}{2}\cdot...\cdot\frac{1}{2}\Gamma(\frac{1}{2})

\displaystyle=\frac{(2n-1)!!}{2^n}\sqrt{\pi}(n\in N^*)

Ⅱ、 \displaystyle \Gamma(n-\frac{1}{2})

\displaystyle=\frac{-2}{2n-1}\Gamma[\frac{1}{2}-(n-1)]

\displaystyle =(-\frac{2}{2n-1})\cdot(-\frac{2}{2n-3})\cdot...\cdot(-\frac{2}{1})\Gamma(\frac{1}{2})

\displaystyle =\frac{(-1)^{n}2^{n}}{(2n-1)!!}\sqrt{{\pi}}(n\in N^*)

⑨Legendre(勒让德)倍量公式

\displaystyle \sqrt{\pi}\cdot\Gamma(2n)=2^{2n-1}\Gamma(n)\Gamma(n+\frac{1}{2})(n\in N^*)

进一步地，可得到

\displaystyle \Gamma(2n)=\frac{2^{2n-1}\Gamma(n)\Gamma(n+\frac{1}{2})}{\sqrt{\pi}}

代入公式⑧-Ⅰ可得，

\displaystyle \Gamma(2n)=\frac{2^{2n-1}\Gamma(n)\frac{(2n-1)!!}{2^n}\sqrt{\pi}}{\sqrt{\pi}}

\displaystyle=2^{n-1}\cdot(2n-1)!!\cdot\Gamma(n)(n\in N^*)

仔细观察，发现这个等式最后可变成刚才的双阶乘公式。

⑩几种可能用得到的积分结论

Ⅰ、 \displaystyle \int_{0}^{+\infty}x^ne^{-\alpha x}dx=\frac{\Gamma(n+1)}{\alpha^{n+1}}

(\displaystyle \alpha、n\in R，\alpha>0，n>-1)

特别地，当n∈N时，这个积分就为

\displaystyle \int_{0}^{+\infty}x^ne^{-\alpha x}dx=\frac{n!}{\alpha^{n+1}}

其中当n=0、1时，有

\displaystyle \int_{0}^{+\infty}e^{-\alpha x}dx=\frac{1}{\alpha}

\displaystyle \int_{0}^{+\infty}xe^{-\alpha x}dx=\frac{1}{\alpha^2}

Ⅱ、 \displaystyle \int_{0}^{+\infty}x^ne^{-\alpha x^2}dx

这个积分三种情况讨论

⑴. \displaystyle \int_{0}^{+\infty}x^ne^{-\alpha x^2}dx=\frac{\Gamma(\frac{n+1}{2})}{2\alpha^{\frac{n+1}{2}}}

(\displaystyle n、\alpha\in R，\alpha>0，n>-1)

⑵. \displaystyle \int_{0}^{+\infty}x^ne^{-\alpha x^2}dx=\frac{(2k-1)!!}{2^{k+1}\alpha^{k+\frac{1}{2}}}\sqrt{\pi}

(n=2k，k\in N)

⑶ \displaystyle \int_{0}^{+\infty}x^ne^{-\alpha x^2}dx=\frac{k!}{2\alpha^{k+1}}

(n=2k+1，k\in N)

Ⅲ、 \displaystyle \int_{0}^{+\infty}e^{-\alpha^2x^2}dx=\frac{\sqrt{\pi}}{2\alpha}(\alpha>0)

Ⅳ、 \displaystyle \int_{0}^{+\infty}x^2e^{-\alpha^2x^2}dx=\frac{\sqrt{\pi}}{4\alpha^3}(\alpha>0)

Ⅴ、 \displaystyle \int_{0}^{+\infty}e^{-\alpha x}sin\beta xdx=\frac{\beta}{\alpha^2+\beta^2}(\alpha>0)

Proof:

\displaystyle LHS=\lim_{A \rightarrow +\infty}{\int_{0}^{a}e^{-\alpha x}sin\beta x}dx

\displaystyle=\lim_{A \rightarrow +\infty}{\frac{e^{-\alpha x}}{\alpha^2+\beta^2}(-\alpha sin\beta x-\beta cos\beta x)∣_{x=0}^{x=A}}

\displaystyle=\frac{\beta}{\alpha^2+\beta^2}=RHS

Q.E.D.

Ⅵ、 \displaystyle \int_{0}^{+\infty}e^{-\alpha x}cos\beta xdx=\frac{\alpha}{\alpha^2+\beta^2}(\alpha>0)

Proof:

\displaystyle LHS=\lim_{A \rightarrow +\infty}{\int_{0}^{a}e^{-\alpha x}cos\beta x}dx

\displaystyle=\lim_{A \rightarrow +\infty}{\frac{e^{-\alpha x}}{\alpha^2+\beta^2}(\beta sin\beta x-\alpha cos\beta x)∣_{x=0}^{x=A}}

\displaystyle=\frac{\alpha}{\alpha^2+\beta^2}=RHS

Q.E.D.

⑪*推广的华里士(Wallis)公式*

在上述计算图3双纽线绕x轴的旋转体积时，得出了一类特殊的定积分计算结论，即

\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{\alpha}\theta \cdot cos^{\beta}\theta d\theta=\frac{\Gamma(\frac{1+\alpha}{2})\Gamma(\frac{1+\beta}{2})}{2\Gamma(1+\frac{\alpha+\beta}{2})}

\displaystyle (\alpha、\beta>-1，\alpha\in R，\beta\in R)

若让α、β分别为偶数或奇数，就得到华里士的推广结论。

接下来还是分情况讨论

Ⅰ、若α、β全为正偶数，W.L.O.G.(不失一般性)设

\displaystyle \alpha=2m,\beta=2n,m、n\in N^*

\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{2m}\theta \cdot cos^{2n}\theta d\theta

\displaystyle=\frac{\Gamma(\frac{1+2m}{2})\Gamma(\frac{1+2n}{2})}{2\Gamma(1+\frac{2m+2n}{2})}

\displaystyle=\frac{\Gamma(m+\frac{1}{2})\Gamma(n+\frac{1}{2})}{2\Gamma(1+m+n)}

\displaystyle =\frac{\frac{(2m-1)!!}{2^m}\sqrt{\pi}\cdot\frac{(2n-1)!!}{2^n}\sqrt{\pi}}{2(m+n)!}

\displaystyle =\frac{(2m-1)!!\cdot(2n-1)!!}{2\cdot2^{m+n}(m+n)!}\pi

\displaystyle =\frac{(2m-1)!!\cdot(2n-1)!!}{(2m+2n)!!}\cdot\frac{\pi}{2}

\therefore\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{\alpha}\theta \cdot cos^{\beta}\theta d\theta

\displaystyle=\frac{(\alpha-1)!!\cdot(\beta-1)!!}{(\alpha+\beta)!!}\cdot\frac{\pi}{2}

例：计算 \displaystyle\int_{0}^{\frac{\pi}{2}}sin^{6}x\cdot cos^8xdx

\displaystyle I=\frac{5!!\cdot 7!!}{14!!}\cdot\frac{\pi}{2}=\frac{5\pi}{4096}

Ⅱ、若α、β不全为偶数，W.L.O.G.(不失一般性)设

\displaystyle \alpha=2m,\beta=2n-1,m、n\in N^*

\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{2m}\theta \cdot cos^{2n-1}\theta d\theta

\displaystyle=\frac{\Gamma(\frac{1+2m}{2})\Gamma(n)}{2\Gamma(1+\frac{2m+2n-1}{2})}

\displaystyle=\frac{\Gamma(m+\frac{1}{2})(n-1)!}{2\Gamma(m+n+\frac{1}{2})}

\displaystyle=\frac{\frac{(2m-1)!!}{2^m}\sqrt{\pi}\cdot(n-1)!}{2\cdot\frac{(2m+2n-1)!!}{2^{m+n}}\sqrt{\pi}}

\displaystyle=\frac{(2m-1)!!\cdot(n-1)!\cdot2^{n-1}}{(2m+2n-1)!!}

\displaystyle =\frac{(2m-1)!!\cdot(2n-2)!!}{(2m+2n-1)!!}

\displaystyle =\frac{(2m-1)!!\cdot(2n-1-1)!!}{(2m+2n-1)!!}

\therefore\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{\alpha}\theta \cdot cos^{\beta}\theta d\theta

\displaystyle=\frac{(\alpha-1)!!\cdot(\beta-1)!!}{(\alpha+\beta)!!}

同理，设

\displaystyle \alpha=2m-1,\beta=2n,m、n\in N^*

也可以得出相同的结论，第Ⅱ种情况只要α或β中的一个为偶数，另一个是奇数即可。

例：计算 \displaystyle\int_{0}^{\frac{\pi}{2}}sin^{3}x\cdot cos^4xdx

\displaystyle I=\frac{2!!\cdot 3!!}{7!!}=\frac{2}{35}

Ⅲ、若α、β全为奇数，W.L.O.G.(不失一般性)设

\displaystyle \alpha=2m-1,\beta=2n-1,m、n\in N^*

\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{2m-1}\theta \cdot cos^{2n-1}\theta d\theta

\displaystyle=\frac{\Gamma(m)\Gamma(n)}{2\Gamma(1+\frac{2m+2n-2}{2})}

\displaystyle =\frac{\Gamma(m)\Gamma(n)}{2\Gamma(m+n)}

\displaystyle =\frac{(m-1)!\cdot(n-1)!}{2(m+n-1)!}

\therefore\displaystyle\int_{0}^{\frac{\pi}{2}}sin^{\alpha}\theta \cdot cos^{\beta}\theta d\theta

\displaystyle=\frac{(\frac{\alpha+1}{2}-1)!\cdot(\frac{\beta+1}{2}-1)!}{2(\frac{\alpha+1}{2}+\frac{\beta+1}{2}-1)!}

\displaystyle=\frac{(\frac{\alpha-1}{2})!\cdot(\frac{\beta-1}{2})!}{2(\frac{\alpha+\beta}{2})!}

例：计算 \displaystyle\int_{0}^{\frac{\pi}{2}}sin^{7}x\cdot cos^9xdx

\displaystyle I=\frac{3!\cdot 4!}{2\cdot8!}=\frac{1}{560}

写到这里，读者不妨用B函数的相关公式去得出考研常用的"点火公式"。

注："点火公式" AKA "华里士(Wallis)公式"。

5.旋转表面积

同理，还是得分以下几种情况讨论。

5.1情况一

记图2双纽线绕x轴旋转一周形成的图形表面积为Sx，则

\displaystyle S_{x}=2\cdot2\pi\int_{0}^{\frac{\pi}{4}}\left| r(\theta)sin\theta \right|\sqrt{[r(\theta)]^2+[r'(\theta)]^2}d\theta

\displaystyle =4\pi\int_{0}^{\frac{\pi}{4}}\left| a\sqrt{cos2\theta}\cdot sin\theta \right|\sqrt{a^2cos2\theta+a^2\cdot\frac{sin^22\theta}{cos2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{4}}\left| \sqrt{cos2\theta}\cdot sin\theta \right|\sqrt{\frac{cos^22\theta}{cos2\theta}+\frac{sin^22\theta}{cos2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{4}}\left| \sqrt{cos2\theta}\cdot sin\theta \right|\sqrt{\frac{1}{cos2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{4}}sin\theta d\theta

\displaystyle =(4-2\sqrt2)\pi a^2

5.2情况二

记图2双纽线绕y轴旋转一周形成的图形表面积为Sy，则

\displaystyle S_{y}=2\cdot2\pi\int_{0}^{\frac{\pi}{4}}\left| r(\theta)cos\theta \right|\sqrt{[r(\theta)]^2+[r'(\theta)]^2}d\theta

\displaystyle =4\pi\int_{0}^{\frac{\pi}{4}}\left| a\sqrt{cos2\theta}\cdot cos\theta \right|\sqrt{a^2cos2\theta+a^2\cdot\frac{sin^22\theta}{cos2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{4}}\left| \sqrt{cos2\theta}\cdot cos\theta \right|\sqrt{\frac{1}{cos2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{4}}cos\theta d\theta

\displaystyle =2\sqrt2\pi a^2

5.3情况三

记图3双纽线绕x轴旋转一周形成的图形表面积为Sx，则

\displaystyle S_{x}=2\cdot2\pi\int_{0}^{\frac{\pi}{2}}\left| r(\theta)sin\theta \right|\sqrt{[r(\theta)]^2+[r'(\theta)]^2}d\theta

\displaystyle =4\pi\int_{0}^{\frac{\pi}{2}}\left| a\sqrt{sin2\theta}\cdot sin\theta \right|\sqrt{a^2sin2\theta+a^2\cdot\frac{cos^22\theta}{sin2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{2}}\left| \sqrt{sin2\theta}\cdot sin\theta \right|\sqrt{\frac{1}{sin2\theta}}d\theta

\displaystyle =4\pi a^2\int_{0}^{\frac{\pi}{2}}sin\theta d\theta

\displaystyle =4\pi a^2

按照对称性，图3双纽线绕y轴旋转一周形成的图形表面积为，

S_{y}=S_{x}=4\pi a^2

6.总结

到这里，有关双纽线的部分数据就整理至此。

在做二重积分的习题时，偶尔会见到几个关于双纽线与其它曲线相结合的积分区域，特别要注意图2中的双纽线θ的范围。

关于双纽线的几何应用。个人而言，如果是期末考试且考试科目是高等数学(上)，大部分高校不会出现让你去计算双纽线弧长、旋转体积；如果是考研(统考数学)，也不会出现让你去计算双纽线弧长和图3中双纽线绕x、y轴的旋转体积，因为这两个要用到Γ、B函数。

注：如果你是考研er要参加统考数学(代号：301-303)考试，建议适当了解下Γ函数及其相关公式、结论。

那么在考研数学中，图2中双纽线的旋转体积会不会考呢？

答：依本人"愚见"，统考数学中出题的可能性不大。从本篇幅中计算图2双纽线绕x、y轴的旋转体积过程来看，计算过程看似在考研数学的范围内，但不太好命题，命题的质量需充分考虑题自身的难度和参考者群体能力水平。话说简单点，如果考试中出现这种题，不管是选择、填空、解答题，可能会导致对考生的区分度太小。如果80%左右的考生知道极坐标曲线旋转体积计算公式的话，个人认为，这种题从某种意义上是可以出现在试卷上的。

如果某年考研数学的试卷上出现了关于图2双纽线旋转体积之类的题，只可能得出一个结论：就是负责考研统考数学的那几个命题老头不按套路出牌！

开个玩笑而已，考研数学命题组每年出几张试卷给怀着希望与梦想上岸的莘莘学子，这个出题过程艰辛且不容易。在这里，给考研数学命题组们点个赞！

注：难度较大或较小的题目，区分度通常较小；中档题区分度较大。因此，一张试卷得考虑众多方方面面因素，而不是随便命题草草了事。

至此，关于"内容概要"中提到的常用曲线，若还有关于曲线的其它性质，请广大网友在评论区留言，本人看到后会选择性对文章进行补充。

望网友补充的曲线性质与曲线的相关数据尽量与考研数学方面相关。

由于篇幅过长，本系列将分成若干篇幅去汇总。

文中若有错误的地方，恳请广大读者、网友们在评论区指正，在下表示万分感谢。

In The End.

Thanks for reading!